MNIST | 基于k-means和KNN的0-9数字手写体识别

概要： 本实验是在实验“kaggle|基于k-means和KNN的语音性别识别”、实验“MNIST|基于朴素贝叶斯分类器的0-9数字手写体识别”以及实验“算法|k-means聚类”的基础上进行的，把k-means聚类和CNN识别应用到数字手写体识别问题中去。有关MINIST数据集和kmeans+KNN的内容可以先看我的上面三篇博文，本实验的代码依然是MATLAB。
关键字： 数字手写体识别; k-means; KNN; MATLAB; 机器学习

1 背景说明

   我在我的上上篇博文中提到会把kmeans聚类算法用到诸如语音性别识别和0-9数字手写体识别等具体问题中去，语音性别识别的实验已经在11月2号完成，现在来填0-9数字手写体识别的坑。由于本篇博客承接了我之前若干篇博客，而MNIST数据集、kmeans以及KNN算法的原理和用法等内容均已在之前提到过，所以这里不再专门说明。

2 算法原理

   可以将本次实验思路概括如下：

   S1：训练时，将训练集中0-9对应的数据各聚成k类，共计10k个聚类中心；
   S2：验证时，计算每一条待识别的数字到10k个聚类中心的距离并将这10k个聚类中心按照离待识别数字的距离由小到大排序，选择序列的前K项，统计这K个聚类中心各自属于0-9中的哪个数字，拥有聚类中心最多的数字就是待识别的数字。当K=1时，距离待识别数字最近的聚类中心所对应的数字就是待识别的数字。

3 代码实现

3.1 文件目录

   文件目录如图1所示。

图1 所需文件列表

 
   其中，code文件夹里的代码文件是实验“算法|k-means聚类”中的9个.m文件，digits中的资源文件是实验“MNIST|基于朴素贝叶斯分类器的0-9数字手写体识别”中的文件夹matdata里的20个.mat文件，包括10个训练集和10个测试集。这些文件的内容在对应博客中都有详细介绍。

   源文件digit_recog_train.m和digit_recog_validate.m分别为训练代码和验证代码，本别实现本博客第2章“算法原理”中的S1和S2的功能。其他三个.mat文件都是所需数据包，DIGITS是上述20个.mat数据包的集合(为了方便后续代码的书写)，cluster_C.mat和cluster_idx.mat分别是函数mykmeans.m的前两项返回值，详情请见实验“算法|k-means聚类”。

3.2 核心代码

   核心代码仍然是训练(kmeans聚类)、识别(KNN判断类别)两步走。首先是kmeans聚类的代码：

%% 聚类
k=1000;
errdlt = 0.5;
cluster_idx = cell(10,1);
cluster_C = cell(10,1);
for i=1:10
    [cluster_idx{i},cluster_C{i},~,~,~] = mykmeans(DIGITS{i+10}.Data_train,k,1,errdlt);
    fprintf('数字%d的训练集聚类完成.\n',i);
end
save('cluster_idx.mat','cluster_idx');
save('cluster_C.mat','cluster_C');
save('DIGITS.mat','DIGITS');

   接着是KNN判断类别的代码：

%% KNN识别/分类
dists = zeros(10*k,2);
for i=1:10
    dists((i-1)*k+1:i*k,2) = zeros(k,1)+i*ones(k,1);
end
RESULTS_num = zeros(10,10);
probnum = zeros(10,1);
K = 1;
% 对每一种数字(共0-9计十个数字)
for category=1:10
    % 每一种数字的测试样本数量
    for i=1:size(DIGITS{category,1}.Data_test,1)    
        % 将每条测试样本拓展成100行,方便计算和比较与聚类中心的距离
        temp = repmat(DIGITS{category,1}.Data_test(i,:),10*k,1);
        dists(:,1) = sum((temp-centers(:,1:28*28)).^2,2);
        [B,ind] = sort(dists(:,1));
        ind = ind(1:K,1);
        % 判断最近的k个中心是哪个数字的中心
        for j=1:K
            switch dists(ind(j,1),2)
                case 1
                    probnum(1) = probnum(1)+1;
                case 2
                    probnum(2) = probnum(2)+1;
                case 3
                    probnum(3) = probnum(3)+1;
                case 4
                    probnum(4) = probnum(4)+1;
                case 5
                    probnum(5) = probnum(5)+1;
                case 6
                    probnum(6) = probnum(6)+1;
                case 7
                    probnum(7) = probnum(7)+1;
                case 8
                    probnum(8) = probnum(8)+1;
                case 9
                    probnum(9) = probnum(9)+1;
                case 10
                    probnum(10) = probnum(10)+1;
            end
        end
        [~,test_rslt] = max(probnum);
        RESULTS_num(category,test_rslt) = RESULTS_num(category,test_rslt)+1;
        probnum = zeros(10,1);          % 千万不养忘了让 probnum 归零！！！
    end
    fprintf('数字%d的测试集已测试完成.\n',category);
end

   当然，最后别忘了计算识别正确率：

%% 由概数计算识别概率
% 0-9各自的概率
RESULTS_prob = zeros(10,10);
for raw=1:10
    if sum(RESULTS_num(raw,:))~=size(DIGITS{raw,1}.Data_test,1)
        fprintf('数字%d测试有误.\n',category);
        break;
    else
        for col = 1:10
            RESULTS_prob(raw,col) = RESULTS_num(raw,col)/sum(RESULTS_num(raw,:));
        end
    end
end
% 总的概率
total_num = 0;
for s=1:10
    total_num = total_num+RESULTS_num(s,s);
end
total_prob = total_num/sum(sum(RESULTS_num));

   具体代码我就不讲解了，相信看过我之前博客的读者应当已经熟悉了我的书写和命名风格。而且本质上这些都是二维数组操作，并没有什么新花样。

4 实验与结果分析

   在不考虑对MNIST数据集做预处理的情况下，影响实验结果的主要因素仍是2点：

   1-聚类数 k 的选取；
   2-最邻近采信范围 K 的选取；

   如果非要考虑得全面一点，那可以参见实验“MNIST|基于朴素贝叶斯分类器的0-9数字手写体识别”的第四章，那里对“帧尺寸”等预处理的概念作了比较详细的解说。但是在本实验中，本着“抓大放小”和“处理问题需抓主要矛盾”的指导思想，我们只考虑上述两点因素。

   在训练阶段结束后，以取k等于10为例，得到如图2所示的100个聚类中心对应数字的图像：

图2 100个聚类中心

 
   调整参数k和K的值进行了一些列实验，得到如图3所示的结果：

图3 实验结果

 
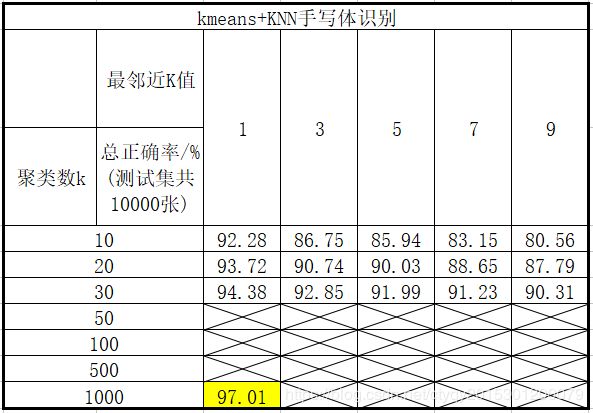
   根据图3的结果，至少可以得到如下结论：

   1-总地来说，0-9数字手写体识别正确率随着k值的增加和K值的减小而提高；
   2-在实验所取得数据范围内，当k=1000，K=1时，0-9数字手写体整体识别正确率最高，达到了97.01%。

   图3中打叉的空格表示未做测试，因为耗时实在是太大。若全都测试一遍太费事，而定性规律已经找出来了，故没有必要再做下去。以k=1000，K=1为例，所需要的训练耗时约为57分钟，验证/识别耗时约为12分钟。具体耗时如图4所示：

图4(1) k=1000，K=1时的训练耗时 图4(2) k=1000，K=1时的验证耗时

 
   由于测试集总计有10000张图片，这样算下来识别一张数字手写体图片所需要的时间约为70ms，这在较高性能的DSP处理器上是可以实现的，且耗时也是可以接受的。

   显然，只看总体识别正确率过于粗糙，因此我还对0-9各自的识别正确率做了统计，如图5所示是k=1000，K=1时0-9各个数字的识别正确率/正确量。其中[行,列]=[D1,D2]表示数字D1被识别为数字D2的数量和概率，第1-10行/列分别表示数字0-9。

图5(1) k=1000，K=1时0-9的识别正确量 图5(2) k=1000，K=1时0-9的识别正确率

 
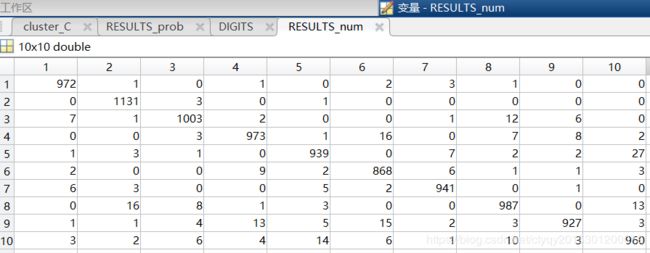
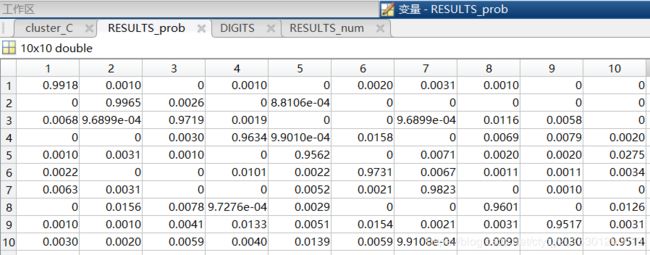
   对图5稍作分析则至少可得如下几点结论：

   1-坐标[1,7]是第1行中除坐标[1,1]外的最大数表明数字0在被错识别时更容易被错识别为数字6；
   2-从第2行看数字1不容易被错识别为其他数字；
   3-坐标[3,8]是第3行中除坐标[3,3]外的最大数表明数字2在被错识别时更容易被错识别为数字7；
   4-坐标[4,6]是第4行中除坐标[4,4]外的最大数表明数字3在被错识别时更容易被错识别为数字5；
   5-坐标[5,10]是第5行中除坐标[5,5]外的最大数表明数字4在被错识别时更容易被错识别为数字9；
   6-坐标[6,4]是第6行中除坐标[6,6]外的最大数表明数字5在被错识别时更容易被错识别为数字3；
   7-坐标[7,1]是第7行中除坐标[7,7]外的最大数表明数字6在被错识别时更容易被错识别为数字0；
   8-坐标[8,2]是第8行中除坐标[8,8]外的最大数表明数字7在被错识别时更容易被错识别为数字1；
   9-坐标[9,6]是第9行中除坐标[9,9]外的最大数表明数字8在被错识别时更容易被错识别为数字5；
   10-坐标[10,5]是第10行中除坐标[10,10]外的最大数表明数字9在被错识别时更容易被错识别为数字4；
   11-上述错识别的状况均与生活经验吻合。

5 后记

   MNIST是一个经典的测试算法性能的数据集，虽然说已经被“用烂了”，但是在本实验中仅凭传统方法就能将识别正确率提升到97%却也是挺让人惊喜的，这比实验“MINIST|基于朴素贝叶斯分类器的0-9数字手写体识别”中用朴素贝叶斯方法得到的约84%的正确率高多了，而且运算量实际上也没有增加多少(朴素贝叶斯方法也需要较大量的运算)。以后学习到别的算法时，也都可以尝试应用到MINIST上看看效果如何。

   最后再说明一下本实验的先导实验是实验“kaggle|基于k-means和KNN的语音性别识别”、实验“MNIST|基于朴素贝叶斯分类器的0-9数字手写体识别”以及实验“算法|k-means聚类”，希望读者也能去看一看。

   由于我已在之前的博客中提供了与k-means和MNIST数据集有关的下载链接，所以这里只提供函数digit_recog_train.m和digit_recog_validate.m的下载链接。

   转载时务必注明来源及作者。尊重知识产权从我做起。

   代码已上传至网络，欢迎下载，密码是y08b。