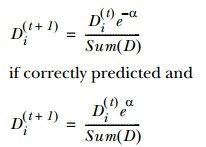机器学习理论与实战(七)Adaboost
Adaboost也是一种原理简单,但很实用的有监督机器学习算法,它是daptive boosting的简称。说到boosting算法,就不得提一提bagging算法,他们两个都是把一些弱分类器组合起来来进行分类的方法,统称为集成方法(ensemble method),类似于投资,“不把鸡蛋放在一个篮子”,虽然每个弱分类器分类的不那么准确,但是如果把多个弱分类器组合起来可以得到相当不错的结果,另外要说的是集成方法还可以组合不同的分类器,而Adaboost和boosting算法的每个弱分类器的类型都一样的。他们两个不同的地方是:boosting的每个弱分类器组合起来的权重不一样,本节的Adaboost就是一个例子,而bagging的每个弱分类器的组合权重是相等,代表的例子就是random forest。Random forest的每个弱分类器是决策树,输出的类别有多个决策树分类的类别的众数决定。今天的主题是Adaboost,下面来看看Adaboost的工作原理:
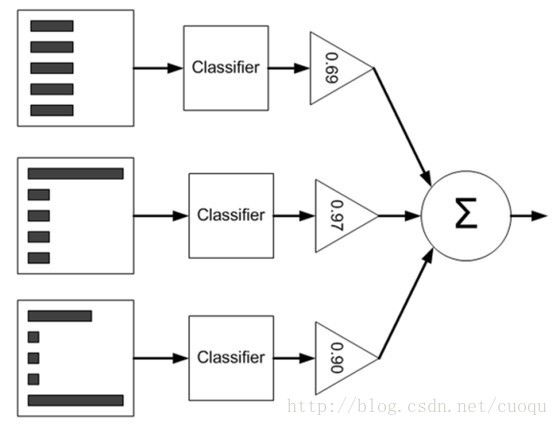
既然Adaboost的每个弱分类器的类型都一样,那么怎么组织安排每个分类器呢?如(图一)所示:
(图一)
(图一)是Adaboost的原理示意图,左边矩形表示数据集,中间表示根据特征阈值来做分类,这样每一个弱分类器都类似于一个单节点的决策树,其实就是阈值判断而已,右边的三角形对每个弱分类器赋予一个权重,最后根据每个弱分类器的加权组合来判断总体类别。要注意一下数据集从上到下三个矩形内的直方图不一样,这表示每个样本的权重也发生了变化,样本权重的一开始初始化成相等的权重,然后根据弱分类器的错误率来调整每个弱分类器的全总alpha,如(图一)中的三角形所示,alpha 的计算如(公式一)所示:
(公式一)
从(公式一)中也能感觉出来,弱分类器权重alpha和弱分类器分类错误率epsilon成反比,如果不能看出反比关系,分子分母同时除以epsilon就可以了,而ln是单调函数。这很make sense,当然分类器的错误率越高,越不能器重它,它的权重就应该低。同样的道理,样本也要区分对待,样本的权重要用弱分类器权重来计算,其实也是间接靠分类错误率,如(公式二)所示:
(公式二)
其中D表示样本权重向量,有多少个样本就有多少个权重,下标i表示样本索引,而上标t表示上一次分类器训练迭代次数。这样一直更新迭代,一直到最大迭代次数或者整个分类器错误率为0或者不变时停止迭代,就完成了Adaboost的训练。但是这样就可以把样本分开了吗?下面从一组图解答这个问题,如(图二)所示:
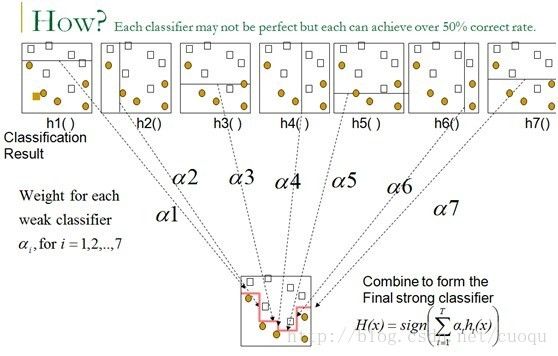
(图二)
由(图二)所示,每个弱分类器Hi可以要求不高的准确率,哪怕错误率是50%也可以接受,但是最后通过线性加权组合就可以得到一个很好的分类器,这点也可以通过错误率分析验证,有兴趣的可以看看:http://math.mit.edu/~rothvoss/18.304.3PM/Presentations/1-Eric-Boosting304FinalRpdf.pdf,想了解为什么alpha的计算如(公式一)的样子,可以看看:http://math.mit.edu/~rothvoss/18.304.3PM/Presentations/1-Eric-Boosting304FinalRpdf.pdf。
这样Adaboost的原理基本分析完毕,下面进入代码实战阶段:
首先来准备个简单数据集:
from numpy import *
def loadSimpData():
datMat = matrix([[ 1. , 2.1],
[ 2. , 1.1],
[ 1.3, 1. ],
[ 1. , 1. ],
[ 2. , 1. ]])
classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
return datMat,classLabels上面有5个样本,接下来就是初始化每个样本的权重,刚开始相等的:
D = mat(ones((5,1))/5)有了样本和初始化权重,接下来的任务就是构建一个弱分类器,其实就是一个单节点决策树,找到决策树每个特征维度上对应的最佳阈值以及表示是大于阈值还是小于阈值为正样本的标识符。代码如下:
def buildStump(dataArr,classLabels,D):
dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
m,n = shape(dataMatrix)
numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))
minError = inf #init error sum, to +infinity
for i in range(n):#loop over all dimensions
rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();
stepSize = (rangeMax-rangeMin)/numSteps
for j in range(-1,int(numSteps)+1):#loop over all range in current dimension
for inequal in ['lt', 'gt']: #go over less than and greater than
threshVal = (rangeMin + float(j) * stepSize)
predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan
errArr = mat(ones((m,1)))
errArr[predictedVals == labelMat] = 0
weightedError = D.T*errArr #calc total error multiplied by D
#print "split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump,minError,bestClasEst注意代码中有三个for循环,这三个for循环其实就是为了完成决策树的每个特征维度上对应的最佳阈值以及表示是大于阈值还是小于阈值为正样本的标识符,这三个要素。其中it,gt分别表示大于和小于,阈值的选择是靠增加步长来需找,最终三者的确定是靠决策树分类错误率最小者决定,每个决策树的分类代码如下,很简单,就是靠阈值判断:
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
retArray = ones((shape(dataMatrix)[0],1))
if threshIneq == 'lt':
retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:,dimen] > threshVal] = -1.0
return retArray有了弱分类器的构造代码,下面来看Adaboost的训练代码:
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m,1))/m) #init D to all equal
aggClassEst = mat(zeros((m,1)))
for i in range(numIt):
bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump
#print "D:",D.T
alpha = float(0.5*log((1.0-error)/max(error,1e-16)))#calc alpha, throw in max(error,eps) to account for error=0
bestStump['alpha'] = alpha
weakClassArr.append(bestStump) #store Stump Params in Array
#print "classEst: ",classEst.T
expon = multiply(-1*alpha*mat(classLabels).T,classEst) #exponent for D calc, getting messy
D = multiply(D,exp(expon)) #Calc New D for next iteration
D = D/D.sum()
#calc training error of all classifiers, if this is 0 quit for loop early (use break)
aggClassEst += alpha*classEst
#print "aggClassEst: ",aggClassEst.T
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))
errorRate = aggErrors.sum()/m
print "total error: ",errorRate
if errorRate == 0.0: break
return weakClassArr,aggClassEst上面的代码中训练过程主要任务就是完成(公式二)中的样本权重D和弱分类器权重alpha的更新,另外还要注意一下,代码中迭代了40次,每次都调用了buildStump,这就意味着创建了40个弱分类器。当模型收敛后,有了样本权重和弱弱弱分类器权重,最后就是对测试样本进行分类,分类代码如下:
def adaClassify(datToClass,classifierArr):
dataMatrix = mat(datToClass)#do stuff similar to last aggClassEst in adaBoostTrainDS
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m,1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\
classifierArr[i]['thresh'],\
classifierArr[i]['ineq'])#call stump classify
aggClassEst += classifierArr[i]['alpha']*classEst
print aggClassEst
return sign(aggClassEst)考虑到有些做学术的为了比较不同机器学习算法的好坏,常常需要画ROC曲线,这里也给出画ROC的代码:
def plotROC(predStrengths, classLabels):
import matplotlib.pyplot as plt
cur = (1.0,1.0) #cursor
ySum = 0.0 #variable to calculate AUC
numPosClas = sum(array(classLabels)==1.0)
yStep = 1/float(numPosClas); xStep = 1/float(len(classLabels)-numPosClas)
sortedIndicies = predStrengths.argsort()#get sorted index, it's reverse
fig = plt.figure()
fig.clf()
ax = plt.subplot(111)
#loop through all the values, drawing a line segment at each point
for index in sortedIndicies.tolist()[0]:
if classLabels[index] == 1.0:
delX = 0; delY = yStep;
else:
delX = xStep; delY = 0;
ySum += cur[1]
#draw line from cur to (cur[0]-delX,cur[1]-delY)
ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b')
cur = (cur[0]-delX,cur[1]-delY)
ax.plot([0,1],[0,1],'b--')
plt.xlabel('False positive rate'); plt.ylabel('True positive rate')
plt.title('ROC curve for AdaBoost horse colic detection system')
ax.axis([0,1,0,1])
plt.show()
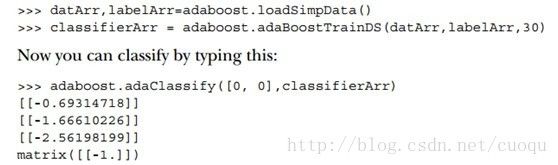
print "the Area Under the Curve is: ",ySum*xStep到此位置,Adaboost的代码也介绍完了,最终程序的运行结果如(图三)所示:
(图三)
而Adaboost的模型ROC运行曲线如(图四)所示:
(图四)
最近MIT的几个人证明了Adaboost可以用一阶梯度的角度来解释,详见链接
参考文献:
[1] machinelearning in action.
[2] http://www.robots.ox.ac.uk/~az/lectures/cv/adaboost_matas.pdf
转载请注明来源:http://blog.csdn.net/cuoqu/article/details/9319459