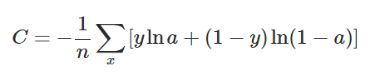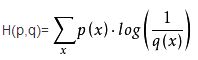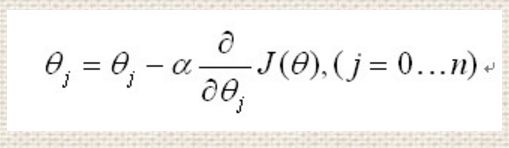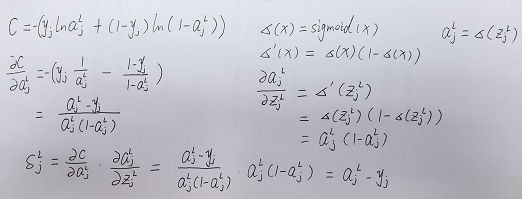C++从零开始实现BP神经网络(一) 原理
BP神经网络的原理,网上已经有很多了,这里我也说说我的看法。
数学规律是我们世界运行的基础,无论是路上跑的汽车,还是看不见的电磁波,都无时无刻的遵从着基础数学,任意事物或行为都可以抽象成一个数学表达式或方程式,如汽车行驶里程就是速度v在时间t上的积分,这种抽象浅显易懂;而对于电磁波而言,描述其的是麦克斯韦方程组,其数学符号繁多,解的方法也较为麻烦,仅仅是理解就耗费了大量的精力,更不用说运用自如了,所幸电磁波还是被人给征服了,能够很方便的使用它进行各类通信。因此,掌握事物的数学规律是运用其的基础,然而对于实际生活中繁多的事件,掌握其准确的数学描述非常的困难,因而也就难以使用它们为我们服务,但是人生来就是挑战不可能的,为了解决这一问题,机器学习应运而生。
机器学习的算法无论多么高深,都是为了尽力描述一种数学规律,传统方式是人对这种规律进行研究,不断的提出模型,又不断的改进,经过几代人的不懈努力后,就可能获得其准确的描述了。这种方式耗时时间长,并且能够进行研究的人少之又少。这时就有人提出,干脆让机器自己去找模型吧,也就是给它输入数据,输出模型,那么如何输出模型呢?假设我们有一组数据如下图所示:
我们可以使用最小二乘法,得到一个函数,使得这个函数距离这些点的距离(所有点到函数的欧式距离)最小,那么这个函数就是描述这些点规律的数学表达式,虽然不够准确,但是仍然描述了大致的方向,若加大数据量,则有可能拟合出更好的函数,使得这个模型更接近于这些点的真实规律,这种方法称为线性拟合或者线性回归。线性拟合可能更接近于统计学模型,但是其确实为机器学习提供了思路,或者说机器学习和统计学的界限是模糊的,二者是相辅相成的。
线性回归的数学模型都是各类参数(特征)的线性组合,线性组合简单来讲就是加减乘除,有以下公式:
也可以简单的写为y=∑wx+b,有了线性回归,那么分类问题也好办了,假设我们将某个阈值为界进行分类,以人的角度来看,肯定是让y大于阈值时候一类,小于阈值时候又一类,这时sigmoid函数便派上用场了,sigmoid函数有点像阶跃函数,其函数图像如下图所示:
将线性回归的输出当做sigmoid的输入,即可得到一个模型:
这个模型就是逻辑回归的模型,可以认为其实广义的线性回归,其将预测值的范围映射到了0和1之间,可以认为对输出赋予了概率的意义,对其进行某个阈值的判断,即可得到0和1的输出,讲了这么多,跟神经网络有什么关系呢,不要急,假设由以下点进行拟合,如果我们单纯使用线性拟合,我们发现总也拟合不好,如果分段函数,则会得到不错的效果,即分别对两段进行线性回归,那么如何将他们写成一个函数呢?不妨加入阶跃函数s1和s2,使得y=(4x-4)s1+(x+5)s2。
其中S1是反向的阶跃函数,S2是正向的阶跃函数,当然,这里的阶跃函数都进行了平移,如下:
使用sigmoid函数代替S1和S2即可近似的表征该分段函数,那么这究竟意味着什么呢?想象一个圆的内接多边形,当这个多边形有4条边时,它一点都不像圆,但是40条边时,我们就几乎无法分辨它和圆的区别了。从微积分的思想来讲,无数个足够小的分段函数足以表征任意函数,如此看来,我们获得了一个可以逼近任意函数的模型,即无数个逻辑回归的组合。在前馈神经网络里,这样一个逻辑回归就是一个神经元。
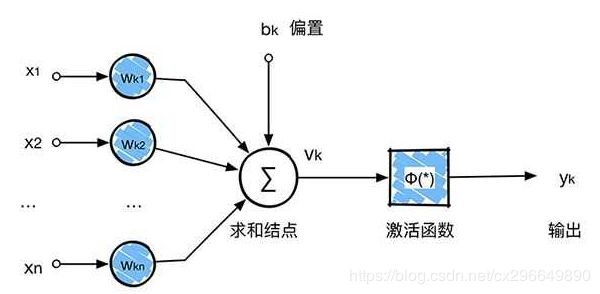
神经元的模型如下:
激活函数可以选择多种,这里选择sigmoid函数,则该神经元可以表征为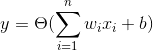 ,其中ω称为权重,b称为偏向,多个神经元组合在一起,就形成了神经网络,神经网络由输入层、隐藏层和输出层组成,最简单的神经网络仅有一层隐藏层,这里以最简单的神经网络为例:
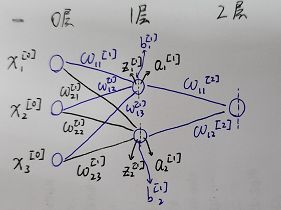
,其中ω称为权重,b称为偏向,多个神经元组合在一起,就形成了神经网络,神经网络由输入层、隐藏层和输出层组成,最简单的神经网络仅有一层隐藏层,这里以最简单的神经网络为例:
先进行符号约定,![]() 为l层中第j个神经元和其前一层中第k个神经元的连接权重,
为l层中第j个神经元和其前一层中第k个神经元的连接权重,![]() 为l层第j个神经元的偏向,
为l层第j个神经元的偏向,![]() 为神经元权重和偏向经过线性组合后的值,
为神经元权重和偏向经过线性组合后的值,![]() 是
是![]() 经过激活函数后的值,这里记激活函数σ,有a=σ(z),则l层第j个神经元的激活值为:
经过激活函数后的值,这里记激活函数σ,有a=σ(z),则l层第j个神经元的激活值为:
拥有了模型之后,还有一个关键问题恣待解决,ω和b未知,数据如何训练才能使得权重和偏向到达最佳值呢?对于一个控制系统,若想稳定的进行调控,闭环负反馈调节必不可少;对于神经网络也是如此,要想让权重和偏向向指定方向移动,必须要把输出重新接回去,这里的重新接回去,就是反向传播算法(backpropagation),此时前馈神经网络变为BP神经网络。
反向传播算法是如何提出的呢?首先了解对于一个数学模型的评价,其最显而易见的方式,就是把数据输入到模型中,看输出值与真正结果的差距或者误差,假设一个模型非常好,其误差为0,我们可以说它是完美的;若误差小于10%,我们说其是优秀的;若误差大于50%,我们认为该模型是不可用的。因此误差可以用来衡量一个模型的好坏,我们称单个样本的误差为损失函数L,整个样本集的误差为代价函数C,其中代价函数可以认为是损失函数在样本集中的平均,即![]() 。
。
在统计学中,均方误差(MSE)能够表征函数拟合的好坏,其是估计值与真实值差值平方和的平均值,即
因此可以选用其作为代价函数,同时代价函数还可以选用交叉熵代价函数CrossEntropyCost,
这里注意交叉熵的定义为:
将其展开可以得到![]() ,注意此处的x是事件,对于神经网络的二分类输出,x有两个事件,即y和1-y,其对应的是a和1-a,即可得到交叉熵代价函数,但是交叉熵代价函数的导出,并不是从此处产生的,交叉熵代价函数的导出方法后续进行介绍。
,注意此处的x是事件,对于神经网络的二分类输出,x有两个事件,即y和1-y,其对应的是a和1-a,即可得到交叉熵代价函数,但是交叉熵代价函数的导出,并不是从此处产生的,交叉熵代价函数的导出方法后续进行介绍。
代价函数已经得到,我们对代价函数进行剖析,C中y为已知值,即训练数据中的标签,只有a是自变量,是最后一层的输出,那么根据神经元的定义和神经网络的结构,影响a的是最后一层的权重、偏向和上一层的激活值,层层上剥,最终发现影响a的是所有神经元权重、偏向和输入值,由于输入值在训练时已知,因此在训练的时候,影响a的只能是所有神经元权重和偏向,进而得出,C是网络中所有神经元权重和偏向的函数,即C(w,b),由于w和b的数量很多,因此C是一个无法画出来的高维函数或者多元函数。上边讲到代价函数评判模型的好坏,我们希望模型经过训练足够好,就需要代价函数足够小,若能找到代价函数的全局最小值,那么模型一定是很棒的。但是事与愿违,多元函数的全局最小值并不容易寻找。
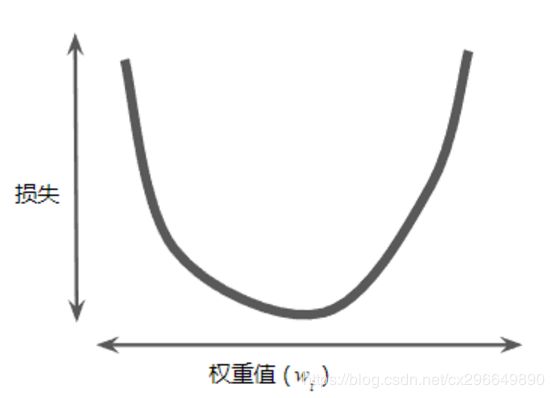
回想一元函数寻找极小值,可以根据斜率(导数),向斜率大的反方向行进即可;对于多元函数,也可以按照这种方式,此时的斜率称为方向导数,方向导数中模最大的称为梯度,而偏导数则是函数沿自变量方向的方向导数。若能沿梯度的反方向进行行进,就一定能找到一个极小值,这种寻找极小值的方法称为梯度下降法。寻找极小值的方法也找到了,但是在沿梯度反方向行进时,每次行进多少或者说每次更新多少呢?观察下图,可以发现,当C不处于极小值时,梯度值较大,越接近极小值,梯度值
则在减小,那么可以用当前权重值减去当前梯度值乘上某个比例来进行权重的更新,即:
这里的比例称为学习率,学习率是个超参数,超参数影响网络的性能,但是却是要在训练前给出的。上述权重更新策略能够使得在远离极小值点时大幅度更新权重,而在接近极小值时小幅度更新权重。
现在,我们已知了代价函数,也知道了让代价函数最小的方法(梯度下降),也知道了每次梯度下降时权重等参数的更新策略,那么唯一的问题就在于如何求得梯度或偏导数。反向传播算法(backpropagation)就是解决这个问题的,其由四个公式组成:
这里边![]() 代表误差,
代表误差,![]() 是对激活值求导,
是对激活值求导,![]() 是激活函数,其中第一个公式BP1说明了最后一层误差是怎么算的,BP2说明了除最后一层外,其它层误差之间的关系,BP3说明了代价函数关于偏向的偏导与误差间的关系,BP4说明了代价函数关于权重的偏导与误差之间的关系。
是激活函数,其中第一个公式BP1说明了最后一层误差是怎么算的,BP2说明了除最后一层外,其它层误差之间的关系,BP3说明了代价函数关于偏向的偏导与误差间的关系,BP4说明了代价函数关于权重的偏导与误差之间的关系。
首先定义每层的误差![]() ,对于每个神经元来讲,就是
,对于每个神经元来讲,就是![]() ,为什么要如此定义误差呢?原因在于我们要使用梯度下降算法,必须要计算出C关于w和b的偏导数,而
,为什么要如此定义误差呢?原因在于我们要使用梯度下降算法,必须要计算出C关于w和b的偏导数,而![]() 为神经元权重和偏向经过线性组合后的值,即Z是w和b的函数,若求得了
为神经元权重和偏向经过线性组合后的值,即Z是w和b的函数,若求得了![]() ,根据链式求导法则,可以很轻易的求出C关于w和b的偏导数,同时仅使用一个一个变量有助于分析问题。
,根据链式求导法则,可以很轻易的求出C关于w和b的偏导数,同时仅使用一个一个变量有助于分析问题。
首先讨论最后一层的误差![]() ,在训练时,我们的已知值是神经网络的输出值
,在训练时,我们的已知值是神经网络的输出值![]() 、当前标签
、当前标签![]() 、激活函数和代价函数,显然是需要使用这些已知条件来计算最后一层误差的,回顾代价函数的定义,其是评判预测值和真实值之间差距的,因此其也由
、激活函数和代价函数,显然是需要使用这些已知条件来计算最后一层误差的,回顾代价函数的定义,其是评判预测值和真实值之间差距的,因此其也由![]() 和
和![]() 组成的,而激活函数
组成的,而激活函数![]() 的输出值就是
的输出值就是![]() ,即
,即![]() 。那么根据链式求导法则可以将误差进行变形,有
。那么根据链式求导法则可以将误差进行变形,有![\delta_{j}^{[L]} =\frac{\partial C}{\partial a_{j}^{[L]}}*\frac{\partial a_{j}^{[L]}}{\partial Z_{j}^{[L]}}](http://img.e-com-net.com/image/info8/8616091171014336abc2667854af2e22.gif) ,观察这个变形,后边的就是激活函数的导函数在
,观察这个变形,后边的就是激活函数的导函数在![]() 处的值,而前边的是代价函数关于a的偏导数在
处的值,而前边的是代价函数关于a的偏导数在![]() 的值。拿交叉熵代价函数举例:
的值。拿交叉熵代价函数举例:
注意此处的代价函数和之前的区别,这里的是针对一个输出神经元而言的,因此去掉了∑和前边的平均系数。至此我们可以顺利的求出最后一层的误差,![\delta_{j}^{[L]} =\frac{\partial C}{\partial a_{j}^{[L]}}*\frac{\partial a_{j}^{[L]}}{\partial Z_{j}^{[L]}}](http://img.e-com-net.com/image/info8/8616091171014336abc2667854af2e22.gif) 仅仅是对一个输出神经元而言的,将其写为矩阵形式,即可得到BP1。
仅仅是对一个输出神经元而言的,将其写为矩阵形式,即可得到BP1。
接着讨论其他层的误差![]() ,有了上一次的经验,我们可以直接写出
,有了上一次的经验,我们可以直接写出![\delta_{j}^{[l]} =\frac{\partial C}{\partial a_{j}^{[l]}}*\frac{\partial a_{j}^{[l]}}{\partial Z_{j}^{[l]}}](http://img.e-com-net.com/image/info8/cd453a099ee64909815c6d21523d0f7c.gif) ,但是似乎并没有什么用处,那么分析现有条件,我们已经可以计算出最后一层的误差了,如果其之间有一定的联系,那么就可以逐层传递,计算出每层的误差,那么是否具有某种关系呢?显然是肯定的,别忘了神经元模型的激活值
,但是似乎并没有什么用处,那么分析现有条件,我们已经可以计算出最后一层的误差了,如果其之间有一定的联系,那么就可以逐层传递,计算出每层的误差,那么是否具有某种关系呢?显然是肯定的,别忘了神经元模型的激活值![]() ,那么对于l层来讲,其l+1层的Z是由
,那么对于l层来讲,其l+1层的Z是由![]() 乘上权重加上偏向算出来的,即
乘上权重加上偏向算出来的,即![]() ,根据链式求导法则再次进行更改,有
,根据链式求导法则再次进行更改,有,根据误差定义,该式第一项就是是l+1层的误差
![]() ,第三项还是激活函数的导数,第二项求导完成后就是l+1层的权重,即
,第三项还是激活函数的导数,第二项求导完成后就是l+1层的权重,即![]() ,可见每层的误差都可以由下一层的误差计算出来,由于最后一层的误差可以首先计算出来,因此,每层的误差就可以从后向前依次计算,这就是为什么称该算法为反向传播的原因,将该结论写成矩阵形式,就可得到BP2.
,可见每层的误差都可以由下一层的误差计算出来,由于最后一层的误差可以首先计算出来,因此,每层的误差就可以从后向前依次计算,这就是为什么称该算法为反向传播的原因,将该结论写成矩阵形式,就可得到BP2.
接下来的问题就简单多了,每层的误差![]() 都可以求出来了,那么我们的目标,求解偏导数
都可以求出来了,那么我们的目标,求解偏导数![]() 和
和![]() 就可以轻松实现了,
就可以轻松实现了,![\frac{\partial C}{\partial w_{ji}^{[l]}}=\frac{\partial C}{\partial Z_{j}^{[l]}}*\frac{\partial Z_{j}^{[l]}}{\partial w_{ji}^{[l]}}=\delta _{j}^{[l]}*a_{ji}^{[l-1]}](http://img.e-com-net.com/image/info8/f4d7934fd6b445f69645844bde24a7ba.gif) ,
,![\frac{\partial C}{\partial b_{j}^{[l]}}=\frac{\partial C}{\partial Z_{j}^{[l]}}*\frac{\partial Z_{j}^{[l]}}{\partial b_{j}^{[l]}}=\delta _{j}^{[l]}](http://img.e-com-net.com/image/info8/6f7a4100421247458c8ca48746ba2246.gif) 。
。
现在为什么使用神经网络,以及BP神经网络是如何运行的已经说完了,接下来就是实际编写代码来实现这个过程。