Yen 的k_shortest paths 算法的C++实现

具体介绍见：https://en.wikipedia.org/wiki/Yen%27s_algorithm

还有具体步骤见：https://blog.csdn.net/sharpdew/article/details/446510?tdsourcetag=s_pctim_aiomsg

我也不知道我对这个算法理解是否完全正确，但是大体的数据结构和逻辑是正确的，希望大家指点，后期我更理解了，会做相应修改。

在这个算法里需要改进的地方是：我没有用堆去插入，这个等有时间再做 

#include
#include
#include
#include
#include 
#include
using namespace std;
static const unsigned int INF(std::numeric_limits::max());
static const unsigned undefined = INF;

class K_Shortest_Path {
public:
	vector> run(
		const unsigned int kPath,					// K Path
		const vector>& NW,		// network
		const unsigned int src,						// source node
		const unsigned int dst);					// destination node
};


//
//结构体用于保存两点之间的最短路径和长度
//
class DijPath
{
public:
	vector onePath;
	int cost;

	bool operator <(const DijPath &n2);

	//判断两条路径是否相等
	bool operator ==(const DijPath &n2);
};


bool DijPath::operator <(const DijPath &n2)
{
	return cost < n2.cost;
}
//判断两条路径是否相等
bool DijPath::operator ==(const DijPath &n2)
{
	if (onePath.size() == n2.onePath.size())
	{
		for (unsigned int i = 0; i < onePath.size(); i++)
		{
			if (onePath[i] != n2.onePath[i])
				return false;
		}

		return true;
	}

	return false;
}


//
//最短路径算法，返回一个DijPath结构体
//
DijPath dijkstra(
	const vector> &NW,
	const int src,
	const int dst
)
{
	//图中节点个数
	unsigned int sizeNW = NW.size(); 

	//知道每一个节点都被访问过结束
	vector visited(sizeNW); 

	//到达dst顶点的最短路径的前一个顶点
	vector prev(sizeNW);    

	//下一个距离当前访问过的最小的一个点
	int minPos = 0; 

	//用于记录每个顶点到源节点的距离，如果最终len[dst]=INF,
	//说明src和dst不可到达，讲cost设置为INF，用于ksp做判断舍弃这条路径
	vector len(sizeNW);

	for (unsigned int i = 0; i < NW.size(); i++) //初始化
	{
		visited[i] = false;  //一开始均被访问
		len[i] = NW[src][i];
		prev[i] = INF;
	}

	//初始节点被设置为访问过
	visited[src] = true;

	for (unsigned int i = 0; i < sizeNW; ++i)  
	{
		unsigned int min = INF;      //记录访问过的节点到没访问过的节点的最小路径长度

		for (unsigned int j = 0; j < sizeNW; ++j)
		{
			if (!visited[j] && min > len[j])
			{
				minPos = j;   //记录找到了下一个节点
				min = len[j];
			}
		}

		visited[minPos] = true;

		for (unsigned int j = 0; j < sizeNW; ++j)
		{
			//如果j节点没有被访问过,且通过j节点发现到其他节点更短的len[j]值
			if (!visited[j] && len[j] > (len[minPos] + NW[minPos][j]))
			{
				prev[j] = minPos;
				len[j] = len[minPos] + NW[minPos][j];
			}
		}
	}

	
	unsigned int beforeVertex = dst;
	//通过一个栈将prev[]中的节点给倒过去，实现正序排列
	stack st;
	while (prev[beforeVertex] != INF)
	{
		st.push(beforeVertex);
		beforeVertex = prev[beforeVertex];
	}
	st.push(beforeVertex);

	//st栈中保存了第二个节点到dst的最短路径的正序
	DijPath oneDijPath;
	oneDijPath.onePath.resize(st.size() + 1);
	oneDijPath.onePath[0] = src;
	for (unsigned int i = 1; !st.empty(); i++)
	{
		oneDijPath.onePath[i] = st.top();
		st.pop();
	}
	oneDijPath.cost = len[dst];  //返回最短路径的值，如果不可到达，设置为INF
	return oneDijPath;
}


//
//用于裁剪掉kSP所有路径中root节点后面的所有的边和当前路径的前一条边
//返回一个vector>的被裁剪后的图
vector> cutEdge(
	const vector>& NW,
	vector< DijPath> kSPCost,
	unsigned int root)
{
	vector>NWCopy = NW;
	for (unsigned int i = 0; i < kSPCost.size(); i++)
	{
		for (unsigned int j = 0; j < kSPCost[i].onePath.size(); j++)
		{
			if (kSPCost[i].onePath[j] == root)
			{
				unsigned int nextVertex = kSPCost[i].onePath[j + 1];
				if (j >= 1)
				{
					unsigned int beforeVertex = kSPCost[i].onePath[j - 1];
					NWCopy[root][beforeVertex] = INF;
				}
				NWCopy[root][nextVertex] = INF;  //设置为不可连接
				break;
			}
		}
	}

	return NWCopy;

}

//
//Yen_k-shortest-path
//
vector> K_Shortest_Path::run(
	const unsigned int kPath,					// K Path
	const vector>& NW,		// network
	const unsigned int src,						// source node
	const unsigned int dst)						// destination node

{
	vector>NWCopy = NW;
	vector< DijPath> kSPCost(1);  //不仅包含最短路径，还包含路径长度
	vector< DijPath>B;    //一个用于记录没有上一代通过裁剪边得到的下一代路径
	DijPath newPath = dijkstra(NW, src, dst);  //第一条最短路径
	vector> kSP;   //返回的路径
	if (newPath.cost==INF)  //判断最开始是否可以到达
	{
		kSP.resize(0);
		return kSP;
	}


	kSPCost[0] = newPath; //用于储存找到的路径
	vectorforwardPath;    //记录裁剪边前面的
	int nowCost;           //用于记录到裁剪掉边前面一段路径的长度

	for (unsigned int k = 1; k < kPath; k++)  //用于找到所有的kPath
	{
		nowCost = 0;

		bool flag = false;
		
		//将这一代中B的节点加到kSP中去，当时必须等待上一代的所有边遍历完成
		for (unsigned int i = 0; i < B.size() && kSPCost.size() < kPath&&kSPCost.size() >= k - 1; i++)
		{

			kSPCost.push_back(B[i]);

			flag = true;

		}

		if (flag)  //如果将B的路径加到A中，就置空B
		{
			B.resize(0);
		}


		//找不到路径了，直接返回
		if (kSPCost.size() < k)
		{
			sort(kSPCost.begin(), kSPCost.end());
			for (unsigned int i = 0; i < kSPCost.size(); i++)
			{
				kSP.push_back(kSPCost[i].onePath);
			}
			return kSP;
		}

		forwardPath.resize(0);

		for (unsigned int i = 0; i < kSPCost[k - 1].onePath.size() - 1; i++)  //用于第k-1条路径所有的边尝试去除去
		{
			forwardPath.push_back(kSPCost[k - 1].onePath[i]);
			if (i != 0)

			{
				unsigned int forwardVertex = kSPCost[k - 1].onePath[i];
				unsigned int nextVertex = kSPCost[k - 1].onePath[i - 1];
				nowCost += NW[forwardVertex][nextVertex];
			}

			NWCopy = cutEdge(NW, kSPCost, kSPCost[k - 1].onePath[i]);


			//找到一条从剪掉边的前面的那个节点到终点的一条最短路径
			DijPath secondPath = dijkstra(NWCopy, kSPCost[k - 1].onePath[i], dst);
			if (secondPath.cost > 100000)//判断两点不可以到达
			{
				continue;
			}

			//找到新的路径
			newPath.onePath = forwardPath;
			for (unsigned int j = 1; j < secondPath.onePath.size(); j++)
			{

				newPath.onePath.push_back(secondPath.onePath[j]);

			}

			newPath.cost = secondPath.cost + nowCost;


			//判断newPath是不是已经存在了

			secondPath.onePath.resize(0);

			DijPath tmp;

			tmp.cost = newPath.cost;

			bool flag = true;

			for (unsigned int j = 0; j < kSPCost.size(); j++)
			{

				tmp.onePath = kSPCost[j].onePath;
				if (tmp == newPath)
				{
					flag = false;   //已经存在了
					break;
				}

			}

			if (flag)  //不存在，加到新的路径中
			{
				B.push_back(newPath);
			}

			if (kSPCost.size() >= kPath)
			{
				sort(kSPCost.begin(), kSPCost.end());
				for (unsigned int i = 0; i < kSPCost.size(); i++)
				{
					kSP.push_back(kSPCost[i].onePath);
				}
				return kSP;
			}
		}

	}

	sort(kSPCost.begin(), kSPCost.end());
	for (unsigned int i = 0; i < kSPCost.size(); i++)
	{
		kSP.push_back(kSPCost[i].onePath);
	}
	return kSP;
}

int main()

{

	const string funcReturn("int");
	const string funcName("main(int argc, char *argv[])");
	try {
		//unsigned int NODE = 5;

		 ////vector> NW(NODE, vector(NODE, 0));
		 //vector> NW = {
		 //	{0, 0, 0, 1, 1}, // A(0)
		 //	{0, 0, 1, 0, 1}, // B(1)
		 //	{0, 1, 0, 1, 1}, // C(2)
		 //	{1, 0, 1, 0, 1}, // D(3)
		 //	{1, 1, 1, 1, 0}, // E(4)
		 //};

		//// NW 2
		vector> NW = {
			{0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0},
			{1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0},
			{1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0},
			{1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0},
			{0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1},
			{0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0},
			{1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0},
			{0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1},
			{0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1},
			{0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1},
			{0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0},
		};
		
		


		for (unsigned int i(0); i < NW.size(); i++) {
			for (unsigned int j(0); j < NW.size(); j++) {
				if (NW[i][j] == 0) {
					NW[i][j] = INF;
				}
			}
		}

		//创建network

		cout << "Network: " << endl;
		for (unsigned int i(0); i < NW.size(); i++) {
			cout << "  > ";
			for (unsigned int j(0); j < NW[i].size(); j++) {
				if (NW[i][j] !=INF)
					cout << "   " << NW[i][j];
				else
					cout << "   " << 0;
			}
			cout << endl;
		}


		// K-Shortest Path
		unsigned int kPath = 10;

		cout << endl << "K-Shortest Path (" << kPath << ")" << endl;
		K_Shortest_Path KSP;
		vector> kSP = KSP.run(kPath, NW, 0, 1);



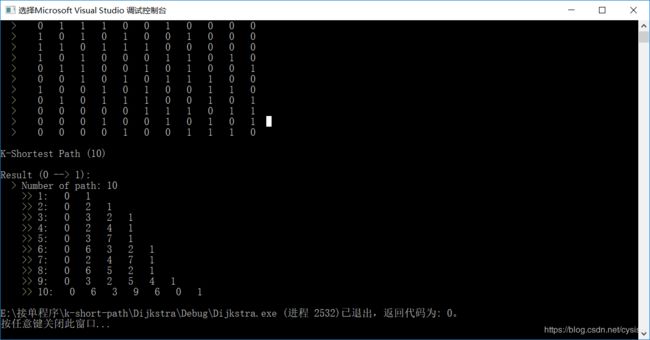
		cout << endl << "Result (0 --> 1): " << endl;
		cout << "  > Number of path: " << kSP.size() << endl;
		for (unsigned int i(0); i < kSP.size(); i++) {
			cout << "    >> " << (i + 1) << ":";
			for (unsigned int j(0); j < kSP[i].size(); j++) {
				cout << "   " << kSP[i][j];
			}
			cout << endl;

		}

		// vector ary1(NODE, 0);
		// vector> ary2(NODE, ary1);

	}


	//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
	// 例外処理
	// エラーが発生した場合にエラーを受け取って表示する処理
	//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

	// 入出力ストリームでの例外処理
	catch (std::ios_base::failure& err) {
		cout << endl << endl;
		cout << "-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-" << endl;
		cout << "Exception : std::ios_base::failure" << endl;
		cout << "  >> " << funcReturn << " " << funcName << endl;
		cout << "Error Content:" << endl
			<< err.what() << endl;
	}

	// 範囲外へのアクセスによる例外処理（実行前）
	catch (std::out_of_range& err) {
		cout << endl << endl;
		cout << "-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-" << endl;
		cout << "Exception : std::out_of_range" << endl;
		cout << "  >> " << funcReturn << " " << funcName << endl;
		cout << "Error Content:" << endl
			<< err.what() << endl;
	}

	// 引数の値が不正な場合の例外処理（実行前）
	catch (std::invalid_argument& err) {
		cout << endl << endl;
		cout << "-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-" << endl;
		cout << "Exception : std::invalid_argument" << endl;
		cout << "  >> " << funcReturn << " " << funcName << endl;
		cout << "Error Content:" << endl
			<< err.what() << endl;
	}

	// 最大の長さを超える長さの値による例外処理（実行前）
	catch (std::length_error& err) {
		cout << endl << endl;
		cout << "-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-" << endl;
		cout << "Exception : std::length_error" << endl;
		cout << "  >> " << funcReturn << " " << funcName << endl;
		cout << "Error Content:" << endl
			<< err.what() << endl;
	}

	// その他の実行前に発生する例外処理（実行前）
	catch (std::domain_error& err) {
		cout << endl << endl;
		cout << "-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-" << endl;
		cout << "Exception : std::domain_error" << endl;
		cout << "  >> " << funcReturn << " " << funcName << endl;
		cout << "Error Content:" << endl
			<< err.what() << endl;
	}

	// 数値演算を行った結果、アンダーフローが発生したときの例外処理（演算関係）
	catch (std::underflow_error& err) {
		cout << endl << endl;
		cout << "-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-" << endl;
		cout << "Exception : std::underflow_error" << endl;
		cout << "  >> " << funcReturn << " " << funcName << endl;
		cout << "Error Content:" << endl
			<< err.what() << endl;
	}

	// 数値演算を行った結果、オーバーフローが発生したときの例外処理（演算関係）
	catch (std::overflow_error& err) {
		cout << endl << endl;
		cout << "-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-" << endl;
		cout << "Exception : std::overflow_error" << endl;
		cout << "  >> " << funcReturn << " " << funcName << endl;
		cout << "Error Content:" << endl
			<< err.what() << endl;
	}

	// 演算処理の過程において、有効な範囲外の値となったときに発生する例外処理（演算関係）
	catch (std::range_error& err) {
		cout << endl << endl;
		cout << "-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-" << endl;
		cout << "Exception : std::range_error" << endl;
		cout << "  >> " << funcReturn << " " << funcName << endl;
		cout << "Error Content:" << endl
			<< err.what() << endl;
	}

	// メモリ確保失敗の例外処理
	catch (std::bad_alloc& err) {
		cout << endl << endl;
		cout << "-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-" << endl;
		cout << "Exception : std::bad_alloc" << endl;
		cout << "  >> " << funcReturn << " " << funcName << endl;
		cout << "Error Content:" << endl
			<< err.what() << endl;
	}

	// 前述していない例外処理を受け取る
	catch (...) {
		cout << endl << endl;
		cout << "-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-" << endl;
		cout << "Exception : unknown" << endl;
		cout << "  >> " << funcReturn << " " << funcName << endl;
	}

	return 0;
}