动态时间规整算法DTW

动态时间规整算法(dynamic time warping,DTW)，最早由日本学者Itakura提出，用于衡量两个时间序列的相似度，也可用于将多个测试序列与标准序列对齐，从而实现序列长度的归一化。

主要应用于语音识别、手势识别、步态识别等领域。

在语言识别领域，同一个词，由于不同个体发音习惯及语速的差异，采集得到的语音信号也呈现出相当大的随机性。比如有的人会把“A”这个音拖得很长，或者把“i”发的很短。通常会表现为整体波形形状相似，但在时间轴上不对齐。在这些复杂情况下，使用传统的欧几里得距离无法有效地求的两个时间序列之间的距离（或者相似性）。DTW通过将序列数据的时间轴扭曲（warping），从而实现时间序列间的对齐。

 

动态时间规整DTW是一个典型的优化问题，它用满足一定条件的的时间规整函数W(n)描述测试模板和参考模板的时间对应关系，求解两模板匹配时累计距离最小所对应的规整函数。

 

实现步骤：

假设我们有两个时间序列Q和C，他们的长度分别是n和m：

若n=m，可直接计算两个序列的距离；若n!=m，最简单的对齐方式就是线性缩放了。把短的序列线性放大到和长序列一样的长度再比较，或者把长的线性缩短到和短序列一样的长度再比较。但是这样的计算没有考虑到语音中各个段在不同情况下的持续时间会产生或长或短的变化，因此识别效果不可能最佳。实践中，更多的是采用动态规划（dynamic programming）的方法，具体如下：

为了对齐这两个序列，我们需要构造一个n x m的矩阵网格，矩阵元素(i, j)表示qi和cj两个点的距离d(qi, cj)（也就是序列Q的每一个点和C的每一个点之间的相似度，距离越小则相似度越高。），一般采用欧式距离，d(qi,cj)=(qi−cj)2。每一个矩阵元素(i, j)表示点qi和cj的对齐。DP算法可以归结为寻找一条通过此网格中若干格点的路径，路径通过的格点即为两个序列进行计算的对齐的点。 

这条路径成为规整路径（warping path），并用W来表示， W的第k个元素定义为wk=(i,j)k，定义了序列Q和C的映射。这样我们有：

满足上面这些约束条件的路径可以有指数个，然后我们感兴趣的是使得下面的规整代价最小的路径：

K用来对长度做补偿。同时定义累积距离r(i,j)。

从(0, 0)点开始匹配这两个序列Q和C，每到一个点，之前所有的点计算的距离都会累加。到达终点(n, m)后，这个累积距离就是我们上面说的最后的总的距离，也就是序列Q和C的相似度。

累积距离γ(i,j)可以按下面的方式表示，累积距离γ(i,j)为当前格点距离d(i,j)，也就是点qi和cj的欧式距离（相似性）与可以到达该点的最小的邻近元素的累积距离之和：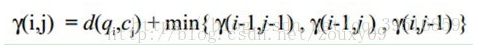 

 

 

示例：

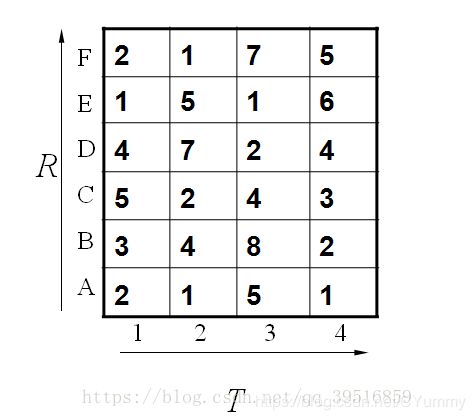
这个例子中假设标准模板R为字母ABCDEF(6个)，测试模板T为1234(4个)。R和T中各元素之间的距离已经给出。如下：

 

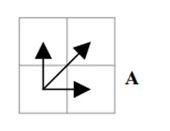
既然是模板匹配，所以各分量的先后匹配顺序已经确定了，虽然不是一一对应的。现在题目的目的是要计算出测试模板T和标准模板R之间的距离。因为2个模板的长度不同，所以其对应匹配的关系有很多种，我们需要找出其中距离最短的那条匹配路径。现假设题目满足如下的约束：当从一个方格((i-1,j-1)或者(i-1,j)或者(i,j-1))中到下一个方格(i,j)，如果是横着或者竖着的话其距离为d(i,j)，如果是斜着对角线过来的则是2d(i,j).其约束条件如下图像所示：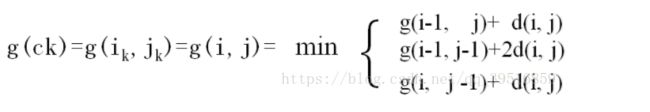 

其中g(i,j)表示2个模板都从起始分量逐次匹配，已经到了M中的i分量和T中的j分量，并且匹配到此步是2个模板之间的距离。并且都是在前一次匹配的结果上加d(i,j)或者2d(i,j),然后取最小值。

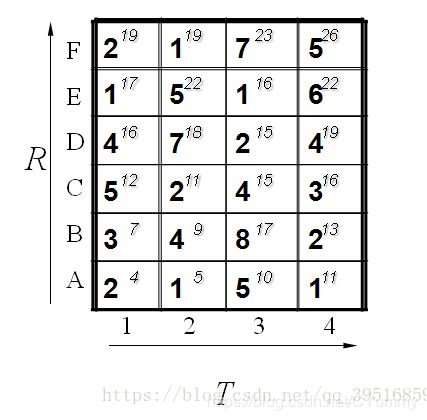
所以我们将所有的匹配步骤标注后如下：

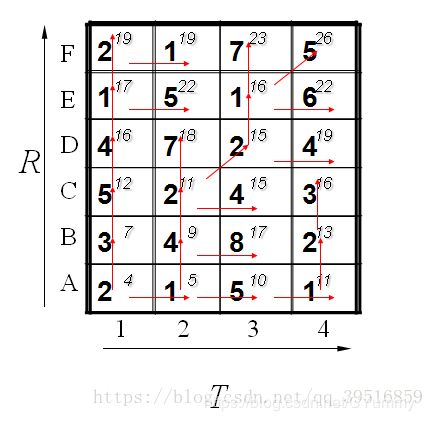
即2个模板直接的距离为26. 我们还可以通过回溯找到最短距离的路径，通过箭头方向反推回去。如下所示：

 

 

 

 

参考：

https://baike.baidu.com/item/动态时间规整/4732354?fr=aladdin

https://blog.csdn.net/qq_39516859/article/details/81705010

https://www.cnblogs.com/luxiaoxun/archive/2013/05/09/3069036.html   (c++)

https://www.cnblogs.com/xingshansi/p/6924911.html   （python）