蒙特卡罗模拟 - python实现
基本原理
蒙特卡罗方法通过抓住事物运动的几何数量和几何特征,利用数字方法来加以模拟,即进行一种数字模拟实验。它是以一个概率模型为基础,按照这个模型所描绘的过程,通过模拟实验的结果,作为问题的近似解。
主要步骤如下:
1.构造或描述概率过程
2.实现从已知概率分布抽样
3.建立各种估计量
示例一:π值的计算
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline
# π的计算
n=30000
r=1.0 #半径
a,b=(0.0,0.0) #圆心
xmin,xmax=a-r,a+r
ymin,ymax=b-r,b+r
x=np.random.uniform(xmin,xmax,n)
y=np.random.uniform(ymin,ymax,n)
fig=plt.figure(figsize=(6,6))
axes=fig.add_subplot(1,1,1)
plt.plot(x,y,'ro',markersize=1)
plt.axis('equal')
d=np.sqrt((x-a)**2 + (y-b)**2)
res=sum(np.where(d<r,1,0))
print('落在圆内的点有%i个' % res)
pi = 4*res/n
print("π的近似值为:",pi)
#绘制圆形
from matplotlib.patches import Circle
circle=Circle(xy=(a,b),radius=r,alpha=0.5,color='r')
axes.add_patch(circle)
plt.grid(True,linestyle='--',linewidth='0.5')
plt.show()
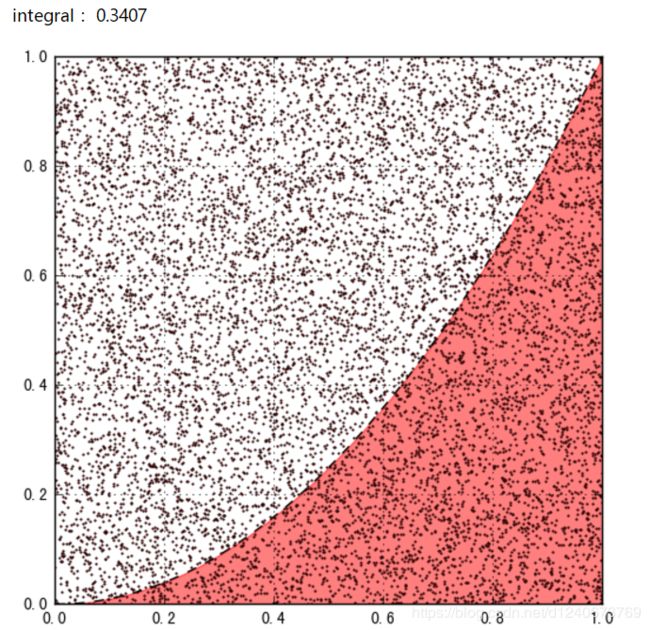
示例二:计算积分y=x^2
n=10000 #投点次数
#矩形区域边界
x_min,x_max=0.0,1.0
y_min,y_max=0.0,1.0
#在矩形区域内随机投点
x=np.random.uniform(x_min,x_max,n)
y=np.random.uniform(y_min,y_max,n)
#创建函数y=x**2
def f(x):
return x**2
#统计落在函数y=x^2图像下方的点的数目
res=sum(np.where(y<f(x),1,0))
#计算定积分的近似值
integral=res/n
print('integral:',integral)
#绘制散点图
fig=plt.figure(figsize=(6,6))
axes=fig.add_subplot(1,1,1)
axes.plot(x,y,'ro',markersize=1)
plt.axis('equal')
#绘制y=x^2面积图
xi=np.linspace(0,1,100)
yi=xi**2
plt.plot(xi,yi,'--k')
plt.fill_between(xi,yi,0,color='r',alpha=0.5,label='area')
plt.grid()