利用python进行数据分析-----第二篇 Numpy 数组 矢量计算 索引 切片 转置 轴对换 文件输入输出
目录
Numpy简介
ndarray 一种多维数组对象
创建ndarray
其他数组创建函数
ndarray的数据类型
数组和标量之间的运算
基本的索引和切片
高维切片索引
布尔值索引
花式索引
数组转置和轴对换
计算矩阵的内积
transpose函数
通用函数:快速的元素级数组函数
两数组取最大
返回整数和小数部分
其他函数
利用数组进行数据处理
将条件逻辑表为数组运算
数学和统计方法
用于布尔型数组的方法
排序
唯一化及其他的集合逻辑
用于数组的文件输出
将数组以二进制格式储存到磁盘
存取文本文件
线性代数
随机数生成
Numpy简介
NumPy是一种通用的阵列处理软件包,旨在有效地操纵任意记录的大型多维数组,而不会为小型多维数组牺牲太多的速度。 NumPy建立在数字代码库的基础上,增加了numarray引入的功能以及扩展的C-API,并且能够创建任意类型的数组,这也使得NumPy适合与通用数据库应用程序连接。
离散傅里叶变换,基本线性代数和随机数生成也有基本功能。
从pypi分发的所有numpy轮都是BSD许可的。
Windows wheels与ATLAS BLAS / LAPACK库链接,仅限SSE2指令,因此可能无法为您的机器提供最佳线性代数性能。 有关替代方案,请参见http://docs.scipy.org/doc/numpy/user/install.html。
----https://pypi.org/project/numpy/
ndarray 一种多维数组对象
Numpy最重一个特点就是其多维数组对象ndarray,ndarray是一个通用的同构数据容器,所有元素必须为相同类型,每个数组都包含用来表示维度大小的元组shape,一个用于说明数组对象的dtype.
创建ndarray
>>> data1 = [2,3,4,5,6]
>>> import numpy as np
>>> arr1 = np.array(data1)
>>> print arr1
[2 3 4 5 6]
>>> arr1
array([2, 3, 4, 5, 6])>>> data2 = [[1,2,3,4],[5,6,7,8]]
>>> arr2 = np.array(data2)
>>> arr2
array([[1, 2, 3, 4],
[5, 6, 7, 8]])
>>> arr2.ndim
2
>>> arr2.shape
(2L, 4L)其他数组创建函数
| 函数 | 说明 |
| array | 输入的 列表、元组、数组、或其它序列类型转换为ndarray,推断出或显示指定dtype,默认直接复制输入数据 |
| asarray |
将输入转换为asarray,输入是ndarray不进行复制 |
| arange | 内置range,返回为ndarray |
| ones,ones_like | 根据指定形状创建一个全1数组,one_like以另一个数组为参数,并根据其形状和dtype创建一个全1数组 |
| zeros,zeros_like |
全0数组 |
| empty,empty_like | 创建新数组,只分配内存空间,但不填充任何值 |
| eye,identity | 创建一个N*N单位矩阵。 |
ndarray的数据类型
dtype包含将ndarray内存解释为特定数据类型需要的信息,多数情况下,他们直接映射到响应机器表示。
| 类型 | 类型代码 | 说明 |
| int8、uint8 | i1、u1 | 有符号和无符号的8位(1个字节)整数 |
| int16、uint16 | i2、u2 | 有符号和无符号的16位(2个字节)整数 |
| int32、uint32 | i4、u4 | 有符号和无符号的32位(4个字节)整数 |
| int64、unint64 | i8、u8 | 有符号和无符号的64位(8个字节)整数 |
| float16 | f2 | 半精度浮点数 |
| float32 | f4或f | 标准的单精度浮点数 |
| float64 | f8或d | 标准的双精度浮点数 |
| float128 | f16或g | 扩展精度浮点数 |
| complex64、complex128、complex256 | c8、c16、c32 | 分别用两个32位、64位或128位浮点数表示的复数 |
| bool | ? | 存储True和False值的布尔类型 |
| object | O | Python对象类型 |
| string_ | S | 固定长度的字符串长度(每个字符1个字节) |
| unicode_ | U | 固定长度的unicode长度(每个字符1个字节) |
数组和标量之间的运算
数组很重要,因为即使你不用编写循环即可对数据执行批量运算,通常叫做矢量化,vectorization,大小相等的数组之间任何的算数运算都将运算应用到元素级。数组与算数运算会将那个标量传播到各个元素。
>>> arr = np.array([[1.,2.,3.],[4.,5.,6.]])
>>> arr
array([[1., 2., 3.],
[4., 5., 6.]])
>>> arr*arr
array([[ 1., 4., 9.],
[16., 25., 36.]])
>>> arr*3
array([[ 3., 6., 9.],
[12., 15., 18.]])
>>> arr**0.5
array([[1. , 1.41421356, 1.73205081],
[2. , 2.23606798, 2.44948974]])基本的索引和切片
下面的一维数组创建和广播,该过程操作的是数据的原始视图,数据不会被复制,视图任何修改都会直接反映到源数组上
>>> arr =np.arange(15)
>>> arr[3:7] = 0
>>> arr
array([ 0, 1, 2, 0, 0, 0, 0, 7, 8, 9, 10, 11, 12, 13, 14])
>>> array_slice = arr[4:6]
>>> array_slice[1] = 999
>>> arr
array([ 0, 1, 2, 0, 0, 999, 0, 7, 8, 9, 10, 11, 12, 13, 14])
>>> array_slice[:] = 888
>>> arr
array([ 0, 1, 2, 0, 888, 888, 0, 7, 8, 9, 10, 11, 12, 13, 14])高维切片索引
>>> add2d=[[1,2,3],[4,5,6],[7,8,9]]
>>> arr2d = np.array(add2d)
>>> arr2d
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>> arr2d[:2,1:]=0
>>> arr2d
array([[1, 0, 0],
[4, 0, 0],
[7, 8, 9]])
布尔值索引
>>> names =np.array(['Bob','Joe','Will','Bob','Will','Joe','Joe'])
>>> data = np.random.randn(7,4)
>>> data
array([[-0.07293883, -0.7612633 , -0.29319602, -0.0042023 ],
[ 2.289825 , -0.79544618, -1.07545136, -0.90398504],
[-0.16304643, -0.32437501, -1.74858425, 0.98331551],
[ 1.38958392, -0.45864779, 0.84023555, -1.21870602],
[ 1.33682575, 1.06778095, 1.97012061, 0.1859616 ],
[ 0.59551277, -1.09129405, 1.1283531 , -1.65953415]])
>>> data[names == 'Bob']
array([[ 0.27565828, 0.76888988, 0.39861839, 1.17158988],
[ 0.8282542 , 1.32392267, -0.04900376, -0.08355354]])
花式索引
迭代数组内元素,作为索引。
花式索引与切片不同的是,总是将数据复制到新数组中
>>> arr = np.empty((8,4))
>>> for i in range(8):
... arr[i] = i
...
>>> arr
array([[0., 0., 0., 0.],
[1., 1., 1., 1.],
[2., 2., 2., 2.],
[3., 3., 3., 3.],
[4., 4., 4., 4.],
[5., 5., 5., 5.],
[6., 6., 6., 6.],
[7., 7., 7., 7.]])
>>> arr[[4,3,0,6]]
array([[4., 4., 4., 4.],
[3., 3., 3., 3.],
[0., 0., 0., 0.],
[6., 6., 6., 6.]])数组转置和轴对换
转置(transpose)是重塑的一种特殊形式,它返回的是源数据的视图,不会进行复制操作,数组还具有T属性
>>> arr = np.arange(15).reshape((5,3))
>>> arr
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14]])
>>> arr = np.arange(15).reshape((3,5))
>>> arr
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
>>> arr.T
array([[ 0, 5, 10],
[ 1, 6, 11],
[ 2, 7, 12],
[ 3, 8, 13],
[ 4, 9, 14]])计算矩阵的内积
>>> arr = np.random.randn(6,3)
>>> arr
array([[ 0.79621331, -0.83430358, -0.80911319],
[ 0.03574342, 1.84386643, 0.0981496 ],
[ 2.57203239, 1.25346891, 0.75237162],
[-0.06301713, -0.64254258, -0.03910239],
[-0.26404073, 0.24409075, -1.62509342],
[-0.68939168, 0.89466497, -0.7718325 ]])
>>> np.dot(arr.T,arr)
array([[7.79953341, 1.98485182, 2.25805555],
[1.98485182, 6.93995684, 0.73701842],
[2.25805555, 0.73701842, 4.46854357]])transpose函数
元组参数的含义为数据填充的顺序。0,1,2即使正常的顺序。1,0,2即使先填充并列数组内容。即使对应reshape函数的2,2,4
二维数组含两个元素,一维数组含两个元素,三级数组含4个元素,生成顺序为:
000 001 002 003
100 101 102 103
010 011 012 013
110 111 112 113
000 001 002 003 010 011 .... 对应
0 1 2 3 4 5 。。。
>>> arr = np.arange(16).reshape((2,2,4))
>>> arr
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
>>> arr.transpose((0,1,2))
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
>>> arr.transpose((0,2,1))
array([[[ 0, 4],
[ 1, 5],
[ 2, 6],
[ 3, 7]],
[[ 8, 12],
[ 9, 13],
[10, 14],
[11, 15]]])
>>> arr.transpose((1,0,2))
array([[[ 0, 1, 2, 3],
[ 8, 9, 10, 11]],
[[ 4, 5, 6, 7],
[12, 13, 14, 15]]])
通用函数:快速的元素级数组函数
>>> import numpy as np
>>> arr = np.arange(10)
>>> arr
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> np.sqrt(arr)
array([0. , 1. , 1.41421356, 1.73205081, 2. ,
2.23606798, 2.44948974, 2.64575131, 2.82842712, 3. ])
>>> np.exp(arr)
array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
2.98095799e+03, 8.10308393e+03])两数组取最大
>>> x = np.random.randn(8)
>>> y = np.random.randn(8)
>>> x
array([-0.26723909, -1.65511147, -0.04990455, -0.42501926, 0.97194785,
0.39073749, 1.06175327, 0.5585866 ])
>>> y
array([ 1.01009041, -1.62671653, 0.23241848, 0.80207752, -0.96744722,
0.16301932, 1.06355945, -0.57478033])
>>> np.maximum(x,y)
array([ 1.01009041, -1.62671653, 0.23241848, 0.80207752, 0.97194785,
0.39073749, 1.06355945, 0.5585866 ])
返回整数和小数部分
>>> arr = np.random.randn(7)*5
>>> arr
array([-7.66209967, 5.64896005, 3.55067973, -8.23018358, 0.16836742,
5.2033361 , 4.0949317 ])
>>> np.modf(arr)
(array([-0.66209967, 0.64896005, 0.55067973, -0.23018358, 0.16836742,
0.2033361 , 0.0949317 ]), array([-7., 5., 3., -8., 0., 5., 4.]))
其他函数
一元ufunc
二元ufunc
利用数组进行数据处理
>>> import numpy as np
>>> points = np.arange(-5,5,0.01)
>>> xs,ys = np.meshgrid(points,points)
>>> xs
array([[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
...,
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99]])
>>> ys
array([[-5. , -5. , -5. , ..., -5. , -5. , -5. ],
[-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
[-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
...,
[ 4.97, 4.97, 4.97, ..., 4.97, 4.97, 4.97],
[ 4.98, 4.98, 4.98, ..., 4.98, 4.98, 4.98],
[ 4.99, 4.99, 4.99, ..., 4.99, 4.99, 4.99]])
>>> import matplotlib.pyplot as plt
Backend TkAgg is interactive backend. Turning interactive mode on.
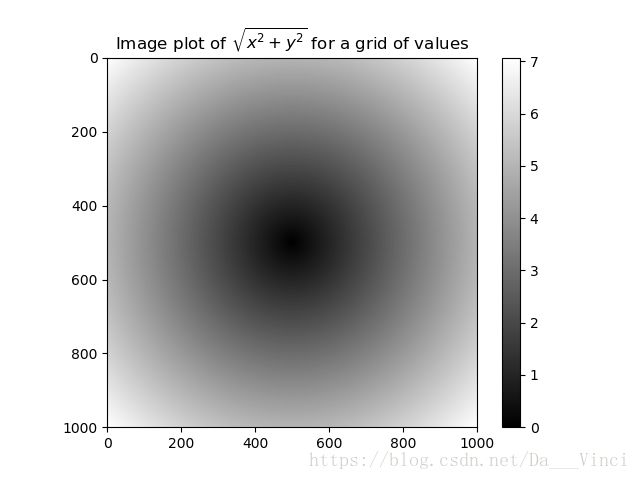
>>> z = np.sqrt(xs **2+ys **2)
>>> plt.imshow(z,cmap=plt.cm.gray);plt.colorbar()
>>> plt.title("Image plot of $\sqrt{x^2+y^2}$ for a grid of values")
Text(0.5,1,'Image plot of $\\sqrt{x^2+y^2}$ for a grid of values')
将条件逻辑表为数组运算
>>> xarr = np.arange(1.1,1.6,0.1)
>>> yarr = np.arange(2.1,2.6,0.1)
>>> cond = np.array([True,False,True,True,False])
>>> result = np.where(cond,xarr,yarr)
>>> result
array([1.1, 2.2, 1.3, 1.4, 2.5])>>> arr = np.random.randn(4,4)
>>> arr
array([[ 0.23409964, -0.05202383, -0.14870559, 0.79573558],
[ 0.55759966, 1.77630082, -1.02818888, 1.9391484 ],
[-1.61633658, 1.22474876, -1.43399786, -1.06554536],
[-0.59160076, -0.97505352, -0.17524749, -1.0561203 ]])
>>> np.where(arr>0,'+','-')
array([['+', '-', '-', '+'],
['+', '+', '-', '+'],
['-', '+', '-', '-'],
['-', '-', '-', '-']], dtype='|S1')
>>> np.where(arr>0,'+',arr)
array([['+', '-0.05202383380539802', '-0.1487055947867779','+'],
['+', '+', '-1.0281888793706875', '+'],
['-1.6163365764782625', '+', '-1.4339978621839753','-1.0655453648238764'],
['-0.5916007573384776', '-0.9750535166810507','-0.17524749337499476', '-1.0561202973574124']], dtype='|S32')
数学和统计方法
>>> arr = np.random.randn(5,4)
>>> arr
array([[ 1.08258166, -1.3217334 , -0.52350247, 0.03050462],
[ 0.11465261, 0.96859544, -0.46915886, -0.64741787],
[-0.71023988, -1.86821324, 0.96951363, 0.75352188],
[ 0.21555276, -1.61668268, 0.87062487, 0.82324383],
[-1.39872473, 1.23463811, -0.12252616, 0.07202626]])
>>> arr.mean()
-0.07713718068750831
>>> arr.sum()
-1.5427436137501662
>>> arr.mean(axis=1)
array([-0.1830374 , -0.00833217, -0.2138544 , 0.0731847 , -0.05364663])
>>> arr.sum(0)
array([-0.69617757, -2.60339578, 0.72495101, 1.03187872])
用于布尔型数组的方法
>>> arr = np.random.randn(100)
>>> arr
array([ 0.34073972, 0.34988851, -0.24126835, -0.42443041, -0.82233812,
-1.21461717, 0.70067547, 0.27200361, -0.78803519, 2.72967498,
0.23312249, 1.18763919, 0.55894897, 2.53258942, 0.36844006,
-0.67321937, 0.49786976, 1.31297101, 0.27737939, 0.39658457,
0.43270061, 1.36756408, 0.52557057, -0.38479557, -0.54033742,
2.36014817, 0.38723984, 1.39320484, -2.14569269, -1.43343552,
0.44446276, -0.42993059, 0.56459971, 0.83332985, 0.98949477,
2.60815978, 1.26375065, -0.88059805, -1.14111095, -1.65499809,
0.63864394, 0.47778961, 0.26342211, -1.76634124, -0.26068543,
0.5670814 , 1.04007051, -0.80613633, -0.32673813, 0.9117205 ,
-0.75458016, 1.25012221, 0.69612343, 1.06615896, 0.13390071,
-0.454111 , 0.14655905, -0.4580414 , 0.07454767, -0.27025394,
-1.04844553, 1.57240204, 1.18913241, -0.78432448, -0.43894174,
0.66986533, 0.20814651, 0.92518062, 0.12918228, 0.27310124,
1.1493472 , 0.85226379, 0.03587044, 0.05448845, 0.82835153,
1.20158862, -2.5518186 , 0.00477461, -2.04586305, -0.67640765,
-0.34065765, -2.03171558, -0.67235383, -1.09601531, -1.89471508,
1.19177494, 0.23241942, 0.34659145, 0.3189491 , -1.78125371,
-0.40714885, 1.07899036, -0.42497074, -2.30353161, 0.63488171,
0.72633715, -0.95954112, 1.3100279 , 1.3475652 , -0.19139045])
>>> (arr>0).sum()
61
>>> bools = np.array([True,False])
>>> bools.all()
False
>>> bools.any()
True
排序
>>> arr = np.random.rand(8)
>>> arr.sort()
>>> arr
array([0.21615835, 0.38790504, 0.48986001, 0.62345955, 0.72247371,
0.76378606, 0.8537614 , 0.98389717])
>>> arr = np.random.rand(5,3)
>>> arr
array([[0.20842559, 0.62874868, 0.09412693],
[0.74471062, 0.8824011 , 0.07132945],
[0.55527621, 0.08276499, 0.68830341],
[0.89926682, 0.55918536, 0.57398518],
[0.3620882 , 0.50525962, 0.14761893]])
>>> arr.sort()
>>> arr
array([[0.09412693, 0.20842559, 0.62874868],
[0.07132945, 0.74471062, 0.8824011 ],
[0.08276499, 0.55527621, 0.68830341],
[0.55918536, 0.57398518, 0.89926682],
[0.14761893, 0.3620882 , 0.50525962]])唯一化及其他的集合逻辑
>>> name = np.array(['Bob','Jon','Tom','Bob','Bob'])
>>> np.unique(name)
array(['Bob', 'Jon', 'Tom'], dtype='|S3')
>>> ints = np.array([1,1,2,3,4,4,5,5])
>>> np.unique(ints)
array([1, 2, 3, 4, 5])>>> value = np.array([2,3,4,5,6,7])
>>> np.in1d(value,[3,5])
array([False, True, False, True, False, False])
用于数组的文件输出
将数组以二进制格式储存到磁盘
>>> arr = np.arange(10)
>>> arr
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> np.save('D:\python\DataAnalysis\some_arr',arr)
>>> np.load('D:\python\DataAnalysis\some_arr.npy')
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])存取文本文件
arr = np.loadtxt('D:\python\DataAnalysis\data\\1.txt',delimiter=',')
arr
array([1., 2., 3., 4., 5., 6., 7.])线性代数
>>> x = np.array([[1,2,3],[4,5,6]])
>>> y = np.array([[7,8],[9,10],[11,12]])
>>> np.dot(x,y)
array([[ 58, 64],
[139, 154]])随机数生成
>>> sample = np.random.normal(size=(4,4))
>>> sample
array([[ 0.77132371, 1.15235977, -0.28535321, -0.58087207],
[-0.09853563, -0.78486528, 0.24612461, 1.22643528],
[ 0.13219711, -2.65805317, 0.05154038, 2.10351203],
[-1.65812602, 0.66330672, 1.62199991, 0.29079451]])