CCF 201803-4 棋局评估（博弈论）

题目来源：http://118.190.20.162/view.page?gpid=T70

问题描述

试题编号：	201803-4
试题名称：	棋局评估
时间限制：	1.0s
内存限制：	256.0MB
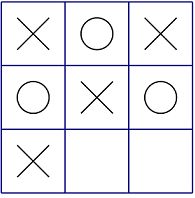
问题描述：	问题描述 　　Alice和Bob正在玩井字棋游戏。 　　井字棋游戏的规则很简单：两人轮流往3*3的棋盘中放棋子，Alice放的是“X”，Bob放的是“O”，Alice执先。当同一种棋子占据一行、一列或一条对角线的三个格子时，游戏结束，该种棋子的持有者获胜。当棋盘被填满的时候，游戏结束，双方平手。 　　Alice设计了一种对棋局评分的方法： 　　- 对于Alice已经获胜的局面，评估得分为(棋盘上的空格子数+1)； 　　- 对于Bob已经获胜的局面，评估得分为 -(棋盘上的空格子数+1)； 　　- 对于平局的局面，评估得分为0； 　　例如上图中的局面，Alice已经获胜，同时棋盘上有2个空格，所以局面得分为2+1=3。 　　由于Alice并不喜欢计算，所以他请教擅长编程的你，如果两人都以最优策略行棋，那么当前局面的最终得分会是多少？ 输入格式 　　输入的第一行包含一个正整数T，表示数据的组数。 　　每组数据输入有3行，每行有3个整数，用空格分隔，分别表示棋盘每个格子的状态。0表示格子为空，1表示格子中为“X”，2表示格子中为“O”。保证不会出现其他状态。 　　保证输入的局面合法。(即保证输入的局面可以通过行棋到达，且保证没有双方同时获胜的情况) 　　保证输入的局面轮到Alice行棋。 输出格式 　　对于每组数据，输出一行一个整数，表示当前局面的得分。 样例输入 3 1 2 1 2 1 2 0 0 0 2 1 1 0 2 1 0 0 2 0 0 0 0 0 0 0 0 0 样例输出 3 -4 0 样例说明 　　第一组数据： 　　Alice将棋子放在左下角(或右下角)后，可以到达问题描述中的局面，得分为3。 　　3为Alice行棋后能到达的局面中得分的最大值。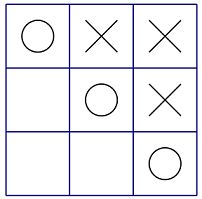 　　第二组数据： 　　Bob已经获胜(如图)，此局面得分为-(3+1)=-4。 　　第三组数据： 　　井字棋中若双方都采用最优策略，游戏平局，最终得分为0。 数据规模和约定 　　对于所有评测用例，1 ≤ T ≤ 5。

------------------------------------------------------------

思路

博弈论模板题，递归搜索状态。

Alice/Bob的每一步都在当前所有可行的行棋位置中选择可以使场上得分最大/小的位置。

具体而言，就是：

1. dfs(s, who)表示当前状态为s（三进制表示整个棋盘），行棋者为who(0:Alice, 1:Bob)情况下该行棋者的最大/小得分

2. 若当前Alice行棋，则遍历s中0的位，将其置为1得到s2, 递归计算dfs(s2,1)，取诸dfs(s2,1)中的最大值为dfs(s,0)的返回值

3. 若当前Bob行棋，则遍历s中0的位，将其置为2得到s2, 递归计算dfs(s2,0)，取诸dfs(s2,0)中的最大值为dfs(s,1)的返回值

4. 当棋局已分出胜负或者棋盘已占满但未分胜负时直接返回

注意点：

1. 棋盘全占满时也能分出胜负；

2. 如果棋盘全占满（无处着棋）且未分胜负，则返回0

------------------------------------------------------------

代码

#include
#include

const short seq[8][3] = {{0,4,8},{2,4,6},{0,1,2},{3,4,5},{6,7,8},{0,3,6},{1,4,7},{2,5,8}};

short myfind(int s, short n)			// s状态下第n个格子的值 
{
	int i, thr = 1;
	for (i=0; i