机器学习高斯混合模型(后篇):GMM求解完整代码实现
《实例》阐述算法,通俗易懂,助您对算法的理解达到一个新高度。包含但不限于:经典算法,机器学习,深度学习,LeetCode 题解,Kaggle 实战。期待您的到来!
01
—
回顾
前面推送中,我们介绍了高斯混合模型(GMM)的聚类原理,以及聚类求解的公式推导,如果您想了解这部分,请参考之前的推送:
机器学习高斯混合模型:聚类原理分析(前篇)
机器学习高斯混合模型(中篇):聚类求解
总结来说,GMM是非常好的聚类利器,它不光能给出样本所属的类别,还能给出属于每个类别的概率,进而转化成得分值,有时所属每个簇的得分值具有重要的意义(意义说明详见之前两篇的推送)。GMM求解的思路本质上是借助最大期望算法的思路来进行求解,关于最大期望算法的原理例子解析,请参考:
机器学习期望最大算法:实例解析
接下来,就到了GMM的EM算法求解的代码实现环节了,如果我们能把一种聚类算法的思路从原理,到公式,再到代码实现,都能走一遍,那么无疑可以表明您对本算法和这一类的算法都有一个全新的理解。手写不掉包代码实现算法的结果,如果能与sklean中的实现基本一致,那么说明才说明您对这个算法正真了解了,在这个编码的过程,将是您对python,Numpy等常用科学计算工具的实践过程,总之意义挺大,锻炼价值也很大。
废话少说,让我们开始GMM模型的EM算法的代码实现之旅吧!
02
—
GMM的EM求解之数据生成
我们先从一维的数据样本的聚类开始说起,先易后难。首先阐述下GMM的EM求解思路。
- 数据准备
我们借助sklearn的API,生成3堆一维高斯分布的数据,一维在此处是指数据的特征只有一个。首先本次实验导入的所有库包括:
import numpy as np
import numpy.linalg as la
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs 生成数据的过程如下:
#生成的簇,和对应的分类
#这是sklearn的聚类结果
#下面自己编码GMM实现聚类,看看与sklearn的结果是够一致
x,label = make_blobs(n_samples=150,n_features=1, centers=3,
cluster_std=[0.01,0.02,0.03],
center_box=(0.1,0.4, 2.0),
random_state=2)
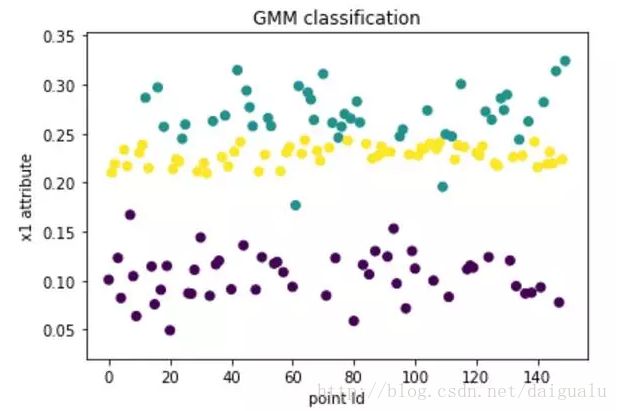
plt.scatter(np.arange(0,150),x[:, 0], marker='o', c=label)
plt.title('GMM classification')
plt.xlabel('point Id')
plt.ylabel('x1 attribute')
plt.show()sklearn生成的满足高斯分布的3簇:
那么,我们一直这些样本点,如何进行正确的聚类呢?也就是能聚类出和上图差不多的效果来。
03
—
EM求解代码解析
1 初始化参数
需要初始化的参数包括:
每个簇的均值,数组的形状参考注释(K by D的意思是K行D列);
协方差(这个需要特别注意,一维高斯是方差,二维以上是协方差,形状也需要特别注意:D by D by K);
每个簇的影响系数
#初始化参数
def initParams(K,D):
#每个簇的中心值:K by D
aves = np.random.rand(K,D)
#每个簇的偏差 D by D by K
sigmas = np.zeros((D,D,K))
###D by D 必须是对称矩阵
sig = np.eye(D)
for k in np.arange(0,K):
sigmas[:,:,k] = sig
#每个簇的影响系数:1 by K
pPis = np.random.rand(1,K)
return aves,sigmas,pPis2 样本点对GMM的贡献系数求解
求解的公式如下,关于这个公式的具体含义,请参考本文开头列出的推送文章。
#样本点对簇的贡献系数
#pPi : 1 by K
#px: N by K
# return value: N by K
def fgamma(px,pPi):
#gamma公式的分子部分
#fenzi: N by K
fenzi = pPi * px
#gamma公式的分母部分
#fenmu: N by 1
fenmu = np.sum(fenzi,axis=1).reshape(N,1)
return fenzi/fenmu一点说明:
在用Numpy求解时,数组的运算可以省掉C++,Java等的很多for循环,可以看求解上面这个公式只需要短短3行代码,可以说说很简洁,但是对于以前使用Java,C++的小伙伴,上手Numpy需要做一个思维转化,同时也要注意标注每个数组的shape,这对于我们后续检查bug非常重要。
3 簇中的样本点的贡献和
从第2步中得出的每个样本点的贡献,然后累加即可:
# 每个簇中的样本点的贡献系数之和
# gam: N by K
# return value: 1 by K
def fNk(gam):
nk = np.sum(gam,axis=0)
return nk.reshape(1,K)上面相当于EM算法的E步,下面总结M步,是利用最大似然估计各个簇的分布参数。
4 每个簇的均值和协方差求解
每个簇的样本和协方差的求解公式如下:
#每个簇的均值
# Nk: 1 by K
# gam: N by K
# x : N by D
#return value: K by D
def faverage(aves,Nk,gam,x):
#print(np.shape(Nk))
for k in np.arange(0,K):
# sum : D
sumd = np.sum((gam[:,k].reshape(N,1)) * x,axis=0)
aves[k,:] = sumd.reshape(1,D)/Nk[:,k]
#每个簇的方差
# Nk: 1 by K
# gam: N by K
# x : N by D
# aves: K by D
#return value: D by D by K
def fsigma(sigmas,Nk,gam,x,aves):
for k in np.arange(0,K):
#shift: N by DA
shift = x - aves[k,:]
#shift_gam: N by D
shift_gam = gam[:,k].reshape(N,1)*shift
#shift2 : D by D
shift2 = shift_gam.T.dot(shift)
sigmas[:,:,k] = shift2/Nk[:,k]
return sigmas5 多维高斯分布的概率密度公式求解
多维高斯分布的概率密度公式见下,式子中 d 表示维数(也就是特征个数),求和符号指:协方差(二维及以上是个方阵)
# D-dimension prob density
# x : N by D
# aves : K by D
# sigmas: D by D by K
# return value: N by K
def fpx(x,aves,sigmas):
Px = np.zeros((N,K))
# coef1 : 1 by 1
coef1 = np.power((2*np.pi),(D/2.0))
for k in np.arange(0,K):
# coef2 : 1 by 1
coef2 = np.power((la.det(sigmas[:,:,k])),0.5)
coef3 = 1/(coef1 * coef2)
# shift: N by D
shift = x - aves[k,:]
# sigmaInv: D by D
sigmaInv = la.inv(sigmas[:,:,k])
epow = -0.5*(shift.dot(sigmaInv)*shift)
# epowsum : N
epowsum = np.sum(epow,axis=1)
Px[:,k] = coef3 * np.exp(epowsum)
return Px6 迭代停止策略
各个样本点的最大似然估计值趋于稳定(小于某个阈值:比如:1e-15),最大似然估计的公式如下:
#迭代求解的停止策略
#px: N by K
#pPi: 1 by K
#Loss function 1 by 1
def fL(px, pPi):
# sub: N by 1
sub = np.sum(pPi*px,axis=1)
logsub = np.log(sub)
curL = np.sum(logsub)
return curL
# stop iterator strategy
def stop_iter(threshold,preL,curL):
return np.abs(curL-preL) < threshold04
—
GMM聚类接口编写
有了以上EM算法的各个函数后,下面可以编写GMM聚类的对外接口了。
# GMM
# return value: N by K
def GMM(x,K):
#loss value initilize
preL = -np.inf;
# aves 每个簇的中心值:K by D
# sigmas 每个簇的偏差 D by D by K
# pPi 每个簇的影响系数:1 by K
aves,sigmas,pPi = initParams(K,D)
while True:
# px: 每个数据所属簇的概率 N by K
px = fpx(x,aves,sigmas)
#print(px)
# 贡献系数 N by K
gam = fgamma(px,pPi)
#每个簇中的样本点的贡献系数之和 1 by K
Nk = fNk(gam)
pPi = Nk/N
# 每个簇的均值 K by D
faverage(aves,Nk,gam,x)
#每个簇的方差 D by D by K
fsigma(sigmas,Nk,gam,x,aves)
# loss function
curL = fL(px, pPi)
#迭代求解的停止策略
if stop_iter(1e-15,preL, curL):
break
preL = curL
return px,aves,sigmas
#返回聚类的结果:N
def classifior(px):
rslt = []
for row in px:
rslt.append(np.where(row==np.max(row)))
return np.array(rslt).reshape(-1)05
—
模拟一维高斯分布的聚类
# K: 簇的个数
# D: 数据的维数(特征数或属性数)
# N:样本点个数
K = 3
D = 1
N = 150
#一维特征的GMM聚类模拟
px,aves,sigmas =GMM(x,3)
mylabel = classifior(px)
#可以看到不掉包的实现与sklearn的模拟结果是基本一致的
plt.scatter(np.arange(0,150),x[:, 0], marker='o', c=mylabel)
plt.title('GMM classification')
plt.xlabel('x1 attribute')
plt.ylabel('x2 attribute')
plt.show()可以看到不掉包的实现与sklearn的掉包实现结果是基本一致的。
一维高斯分布的协方差是方差,是一个数。虽然以上算法能实现多维的高斯分布的聚类,但是鉴于篇幅,明天推送关于多维的高斯分布的聚类的结果展示,协方差,概率密度图等都有着非常重要的应用,并且它们也是非常有意思的。
谢谢您的阅读!
辅助材料:
机器学习储备(13):概率密度和高斯分布例子解析