Course 2-Improving Deep Neural Networks--Week 1

本周涉及数据集划分、偏差-方差、正则化、dropout、归一化输入、梯度消失与爆炸、权重初始化、梯度检验等内容。

1.1 train / dev / test 训练集、验证集、测试集

训练集 training set：是用来训练模型的
验证集 development set \ dev set：是用来选出哪个模型在dev set上表现最好
测试集 test set：用来对验证选出的模型进行无偏估计
对于小数据量的机器学习（10k左右样本量），常用且有效的分法为：训练集、测试集70%-30%划分，训练集、验证集、测试集60%-20%-20%划分。
对于大数据量的机器学习（百万以上样本量），验证集和测试集的比例就会小很多，如训练集、验证集、测试集98%-2%-2%划分，当数据量更大时为99.5%-0.25%-0.25%、99.5%-0.4%-0.1%
由于深度学习需要的数据量很大，数据的来源也很广泛，因此，很多数据源自不同的分布，但有一条经验法则是：必须保证验证集数据和测试集数据的分布相同。
另外，当不需要无偏估计时，我们可以不要测试集，此时只有训练集和验证集。

1.2 bias / variance 偏差、方差

在深度学习误差中，有关bias-variance trade-off 的讨论越来越少，总是分别考虑bias和variance。具体如下：
high bias –> underfitting
high variance –> overfitting
当样本只有两维特征时，我们尚能通过画出决策面来判断偏差和方差，但当样本维数很高时，要判断模型的bias和variance就要借助其他指标了。理解bias和variance的两个关键数据是train set error与dev set error，通过查看这两个数据来判断算法的偏差和方差情况。以下表数据为例，假设最优误差（贝叶斯误差）很小（接近为0）并且训练集和验证集来自同一分布。表中给出了四种情况下的训练集误差和验证集误差，以及它们的偏差和方差情况。我们首先通过查看train set error与最优误差之间的差异来判断算法的bias，如果train set error与最优误差差异很小，则算法为low bias；如果train set error与最优误差差异差异较大，则算法为high bias。然后再通过比较train set error与dev set error的差异来判断算法的variance，如果dev set error与train set error差异很小，则算法为low variance；如果dev set error与train set error差异较大，则算法为high variance。

train set error	dev set error	结论
1%	11%	high variance
15%	16%	high bias
15%	30%	high bias, high variance
0.5%	1%	low bias, low variance

按照之前的理解，高偏差意味着模型的复杂度不够、数据拟合度低，高方差意味着模型的复杂度过高、数据过拟合。那么，针对上表中第三种情况，一个模型同时具有高偏差和高方差意味着什么呢？想象一下在样本空间中，模型对样本空间中的部分数据拟合程度过低，但又对空间中的其他部分数据拟合程度过高，这样，该模型就同时具有高偏差和高方差。

1.3 basic “recipe” for machine learning 机器学习基础

Andrew Ng 在训练神经网络时会用到的基本方法：初始模型训练完成后，首先通过查看train set error来判断算法的bias高不高，如果算法是high bias，那么尝试有更多hidden layers或hidden units 的更大的网络（通常有用）、花更多的时间来训练网络（不一定有用）、尝试新的神经网络架构（不一定有用），直至偏差降低至可接受的数值。然后，通过查看dev set error来判断算法的variance有没有问题，如果算法是high variance，最好的方法就是采用更多的数据，当无法获得更多数据的时候，可以使用regularization，或者可以尝试其他的神经网络架构。这样不断尝试，直到找到一个low bias、low variance的算法。

1.4 regularization 正则化

当你怀疑模型存在overfitting，那么最应该尝试的方法可能是正则化。另一个解决高方差的方法是准备更多的数据，这也是非常可靠的办法，不过因为种种原因，我们无法获得更多的数据。但是，regularization常有助于防止过拟合。正则化，即在代价函数中加入了正则化项，常见的有 L1 正则化项和 L2 正则化项：

L1=λm||w||1

L2=λ2m||w||22

如果使用 L1 正则化，则 w 会变得稀疏。现在在训练神经网络时，越来越多的人学会选择使用 L2 正则化。 λ 称为正则化参数，是另一个超参数，通常使用dev set来配置这个参数，在尝试很多取值后，确定最好的参数。
如何在神经网络中实现 L2 正则化呢？

J(W[1],b[1],…,W[L],b[L])=1m∑i=1nL(y^(i),y(i))+λ2m∑l=1L||W[l]||2

其中，

||W[l]||2=∑i∑j(w[l]ij)2

展开可写为：

J=−1m∑i=1m(y(i)log(a[L](i))+(1−y(i))log(1−a[L](i)))

Jregularized=−1m∑i=1m(y(i)log(a[L](i))+(1−y(i))log(1−a[L](i)))cross-entropy cost+1mλ2∑l∑k∑jW[l]2k,jL2 regularization cost

此时， dW[l]=(frombackprop)+λmW[l] ，所以 W[l] 在参数更新时，可表示为

W[l]=W[l]−αdW[l]=W[l]−α(frombackprop)−αλmW[l]=(1−αλm)W[l]−α(frombackprop)

因此， L2 norm正则化项又称为 权重衰减(weight decay)。
最后说明一下，在计算正则项时，一般都忽略偏置b的正则项，因为它只是众多参数中的一个，影响很小，当然也可以计算，只是对结果的影响可忽略。

1.5 why regularization reduce overfitting

解释一：
对于包括有正则化项的代价函数 J

J(W[1],b[1],…,W[L],b[L])=1m∑i=1nL(y^(i),y(i))+λ2m∑l=1L||W[l]||2

我们的目的是让代价函数 J 最小化。考虑一种极端的情况，正则化参数 λ 很大，为了让 J 最小化，则 ∑Ll=1||W[l]||2 要最小化，即网络中所有权重矩阵 W 的F-范数之和最小化。根据矩阵F-范数的定义，矩阵的F-范数是矩阵中每个元素的平方之和。于是， L2 正则化项的作用就是使网络中的权重趋向于0，从而使网络变得简单，模型复杂度降低，算法方差减小。
解释二：
假设激活函数 g(z)=tanh(z) ，当 |z| 取值很小的时候，可认为 g(z) 所对应的部分是线性的。对于含有正则化项的代价函数，当 λ 变大时， W 会变得相对较小，又因为 z=Wa+b ， z 也会变得相对较小，当 z 落在 g(z) 的线性部分时，激活函数将变成线性激活函数。当每层都大致线性的时候，整个网络的表现就和logistic regression差不多了，退化成了一种简单的网络。
one implementational tip:
当给代价函数加上正则化项后，画出的代价函数曲线就是随着迭代次数的增加单调递减的。如果画出的代价函数没有正则项，只有第一项，那么画出的代价函数可能不是在所有范围内都单调递减。

1.6 Dropout regularization

除了 L2 正则化外，还有一个非常有用的正则化方法称为dropout（随机失活）。dropout会遍历网络中的每一层，并设置网络中各节点被消除的概率，根据概率消除一些神经元，得到一个神经元更少、规模更小的网络，然后使用back-prop训练模型。对于不同的样本，设置每层中各神经元被消除的概率，消除一些神经元。这样，对于每个样本，都采用一个神经元减少后的网络进行训练。
如何实现dropout呢？
目前最常用的时inverted dropout（反向随机失活）。以神经网络中的第3层来说明如何在某一层神经网络中实现dropout。首先，定义向量 d ，那么 d3 就表示第3层的dropout vector：

d3=np.random.rand(a3.shape[0],a3.shape[1])<keep-prop

若 keep-prop=0.8 ，则表示消除任意隐藏单元的概率是0.2。因此， d3 的作用就是生成一个随机矩阵。对应的 a3 为

a3=np.multiply(a3,d3) or a3∗=d3

在做上式计算时，python会把true和false翻译为1和0，过滤掉要消除的神经元。最后，还要对 a3 进行 尺度还原

a3=np.divide(a3,keep-prop) or a3/=keep-prop

上式被称为inverted dropout technique。为什么要进行上式的操作呢？假设第3层上有50个神经元，因此 a3 是50*1或50*m维的，如果保留和消除神经元的概率分别是80%和20%。此时，再来考虑 z[4] ， z[4]=W[4]a[3]+b[4] ，当 a[3] 中有20%的元素置0，即 a[3] 减少了20%，为了不减少 z[4] 的期望值，我们需要用 a[3] 除以0.8来修正消除的20%，这样 a[3] 的期望值就不会改变。inverted dropout的功能就是，无论keep-prop的值是多少， inverted dropout方法通过除以keep-prop，确保 a[3] 的期望值保持不变。
而在测试阶段，我们不需要显式地使用dropout。即，我们只在训练阶段使用dropout。

1.7 understanding dropout

由于dropout会随机消除网络中的一些节点，这样每次迭代时，网络都看起来更小了，而这一效果就和使用了正则化的效果一样。
另外，从单一神经元来看，当使用dropout时，该单元的输入被随机消除，也就是说，该神经元不依赖于任何输入，因为任何输入都有可能被随机消除。这样，与每个输入相关联的权重都比较小，即达到了收缩权重平方范数的效果，与 L2 正则化相似。因此，实现dropout的效果是它能收缩权重，并达到防止过拟合的效果。实现dropout的另一个细节是要设置keep-prob这个超参数的值，它代表每一层上保留单元的比例，因此，keep-prob也可以随着神经层的不同而不同。当担心某一层会出现overfitting时（权重矩阵比较大），就把这一层的keep-prob设置的低一点；当某一层不大可能出现overfitting（权重比重比较小）时，就把keep-prob设置的高一点；当keep-prob设置为1时，该层所有的神经元都会保留，也相当于没有使用dropout。
从技术上讲，我们也可以对输入层使用dropout，这样可以移除一些特征，但通常并不这么做，将keep-prob设置为1是最常用的值，或者设为一个较大的值，如0.9，但是消除一半的特征时不太可能的。
本节课总结：如果担心某些层比较容易发生过拟合，那么就将这一层的keep-prob设置的比较低，这样做的缺点就是，在交叉验证时，超参数的搜索范围比较大，要搜索更多的超参数。另一种可选方法是，在有些层上使用dropout，在有些层上不使用，使用dropout的层只有一个超参数，那就是keep-prob。
dropout在计算机视觉中使用的很多，几乎成了默认的选择。dropout是一种正则化方法，它有助于防止过拟合，因此，除非算法过拟合，不然Ng是不会使用dropout的，所以dropout在其他领域应用很少，主要存在于计算机视觉领域，因为我们没有足够的数据。
dropout的一大缺点就是代价函数 J 不再被很好的定义。每次迭代，都会随机消除一些节点，当我们检查梯度下降的性能时，实际上会发现很困难。而当代价函数被很好定义时，会发现每一次迭代，误差都在降低。这样，我们就失去了调试的工具，画不出代价曲线。这种情况下，Ng通常会先关闭dropout函数，将keep-prob设置为1，运行代码，确保代价函数单调递减，然后再打开dropout函数，这样可以确保在dropout时代码没有引入bug。

1.8 Other regularization methods

• data augmentation 数据扩增
  常见于计算机视觉，对图像进行截取、水平翻转、形变等变换操作。
• early stopping
  在训练模型时，我们希望模型的训练集误差(train set error)，即代价函数 J 不断下降，同时，我们还可以得到模型的验证集误差(dev set error)。通常，验证集误差会先下降，然后上升。early stopping的作用就是找到验证集误差最小时所对应的参数 W ，认为这时的 W 是模型的最佳参数。
  但early stopping还有一个缺点，就是无法独立地处理代价函数优化和过拟合问题。因为提前停止梯度下降，也就是停止了优化代价函数 J （这一点理解的不是太透）。

1.9 normalizing input

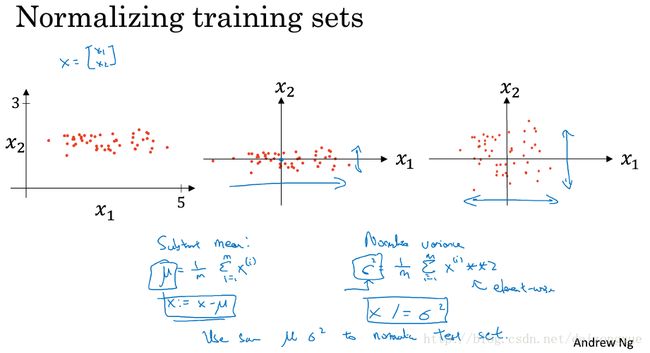
归一化输入是能够加速训练网络的一种技巧，需要两步：
(1) 0-均值化

μ=1m∑i=1mx(i)

x=x−μ

这样，将数据集移动到均值为0的地方。
(2) 归一化方差

σ2=1m∑i=1m(x(i))2

x=xσ2

这样，数据集就成了0均值、方差为1的分布。
tips：标准化验证集和测试集的 μ 、 σ 与标准化训练集的 μ 、 σ 必须相同。

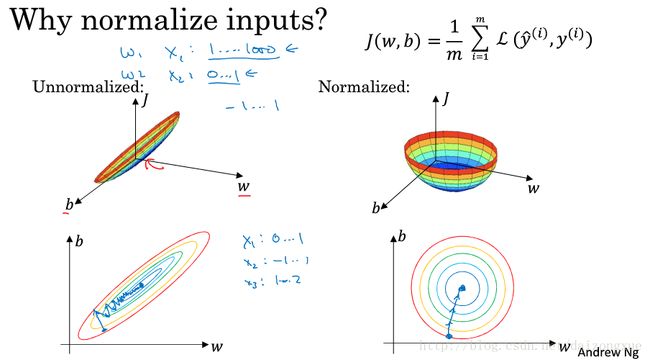
为什么要归一化输入数据呢？，如下图所示，如果输入X在不同的维度上取值范围不一样，比如 x1 是1-1000， x2 是0-1，那么它们对应的权重尺度也是不同的，这样，没有归一化的代价函数曲面就像一个很扁的碗，在这样一个函数曲面上做梯度下降，会导致在一些权重维度上步长较大，而在另一些权重维度上步长较小，导致梯度下降时来回震荡，学习速度慢等问题。但是，若进行了输入归一化后，代价函数曲面就像一个比较圆的碗，在这样的曲面上进行梯度下降可以保证使算法快速到达最优值附近。

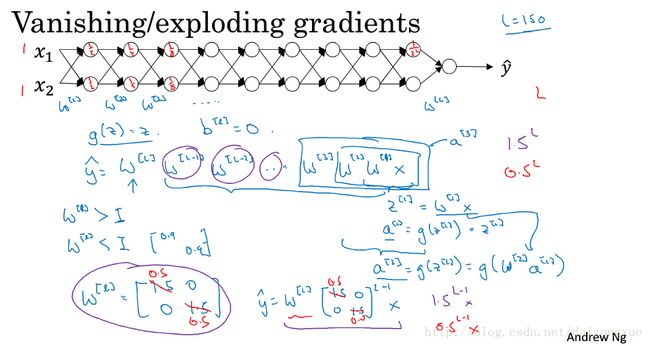
1.10 vanishing/exploding gradients

当深度神经网络很深的时候（即 L 较大时），每层的 W 比单位矩阵略大或略小时，激活函数将以指数级递增或递减。

1.11 weight initialization for deep networks

1.10说明了什么是梯度消失和梯度爆炸。有一个能部分解决梯度消失/爆炸的方法就是谨慎选择神经网络的随机初始化参数。
首先考虑对一个单一的神经元：

z=w1x1+w2x2+...+wnxn

当 n 越大的时候，我们希望 wi 越小。因为我们不想 z 太大而发生梯度爆炸。最合理的方法就是设置 Var(wi)=1n ，n表示神经元的输入特征数量，我们要做的就是设置每层的权重矩阵

W[l]=np.random.randn(shape)∗np.sqrt(1n[l−1])

若是relu激活函数：

Var(wi)=2n

W[l]=np.random.randn(shape)∗np.sqrt(2n[l−1])

若是tanh激活函数（Xavier初始化）：

W[l]=np.random.randn(shape)∗np.sqrt(1n[l−1])

或者：

W[l]=np.random.randn(shape)∗np.sqrt(2n[l−1]+nl)

如果想添加其他的方差，那么这个 方差将作为需要调节的另一个超参数。这样就可训练出一个权重或梯度不会过快增长或消失的神经网络。这也是一个加快训练的技巧。

1.12 numerical approximation of gradients

在实施backprop时，有一个测试叫梯度检验，它可以确保backprop的实现是正确的。为了实现梯度检验，首先要了解梯度的数值检验。即，双边差分的精度比单边差分的精度高。所以，在梯度检验时，我们使用双边差分。

1.13 gradient checking

神经网络的梯度检验：

将参数 W1 , b1 , W2 , b2 … WL , bL reshape成一个大的向量 θ ，这样，代价函数 J(W,b) 就变成了 J(θ) 。同样的将 dW1 , db1 , dW2 , db2 … dWL , dbL 以相同的方式reshape成一个大的向量 dθ 。

实施梯度检验：

for each i ：

dθapprox[i]=J(θ1,θ2,...,θi+ε,...)−J(θ1,θ2,...,θi−ε,...)2ϵ≈dθi

最后判断 dθapprox 与 dθ 是否相近。即，计算下式

||dθapprox−dθ||2||dθapprox||2+||dθ||2

如果 ε=10−7 ：

当上式比值约为 10−7 或更小，那么这个结果就很好

当上式比值在 10−5 以内，这时候就要仔细检查一下

当上式比值在 10−3 以内，就会担心有bug。

1.14 gradient checking implementation notes

• 不要再训练时使用梯度检验，它只用于调试
• 如果算法梯度检验失败，要检查所有的成分来确定bug，即，找出是哪一个 dθapprox[i] 与 dθ[i] 相差太大
• 如果使用了正则化，不要忘记正则项
• 梯度检验不能与dropout同时使用。因为在每次迭代时，dropout会随机让隐藏层的神经元消失，这样就难以计算dropout在梯度下降时的代价函数。所以，通常在梯度检验时不进行dropout，即设置keep-prob=1。在确保算法没问题的时候再打开dropout。
• 在随机初始化的过程中，运行梯度检验，然后训练一会儿后，再运行梯度检验。