多角度看微积分基本定理

微积分基本定理是联系微分学与积分学的桥梁，它是微积分中最基本的公式之一。它证明了微分与积分是可逆运算，同时在理论上标志着微积分完整体系的形成，从此微积分成为一门真正的学科。

微积分基本定理包括：原函数存在定理和牛莱公式。利用原函数存在定理可以很方便地证明牛莱公式。本文只谈原函数存在定理，从三个角度让你更加深入地理解这个重要的定理。

01 物理的角度

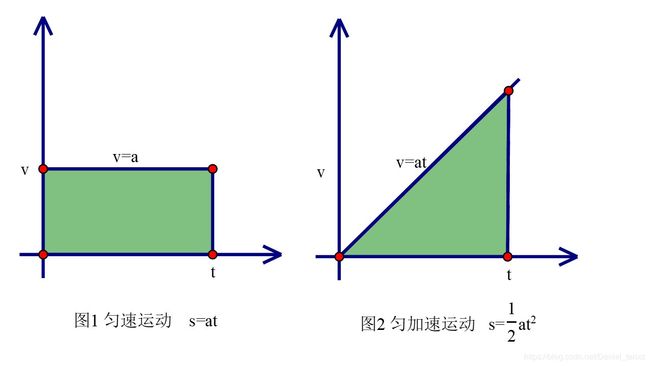
（1）如图1，物体以速度$v=a$作匀速直线运动，$t$时刻的路程为$s=at,$ 从几何上看，等于图中长方形面积；

（2）如图2，物体以加速度a ,初速度为0作匀加速直线运动，$t$时刻的路程为$s=\frac{1}{2}a{t}^2$, 从几何上看，等于图中三角形的面积（思考一下为什么？）；

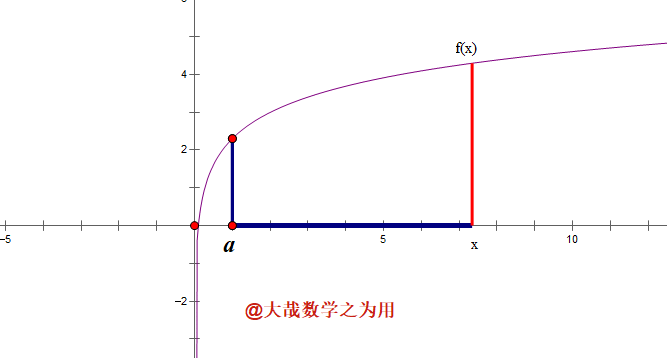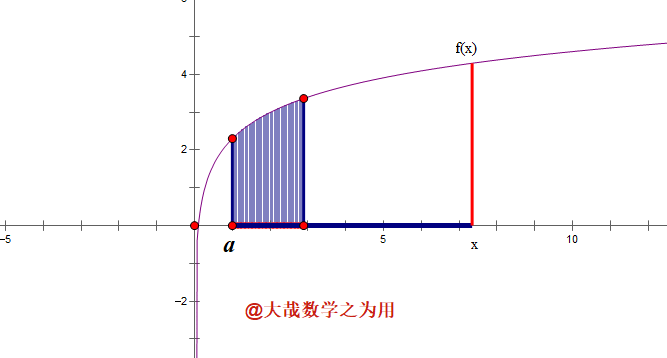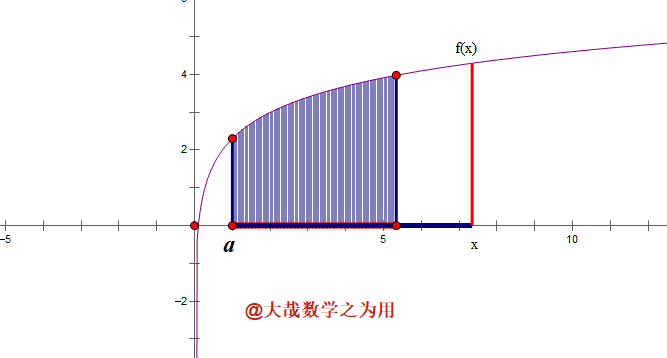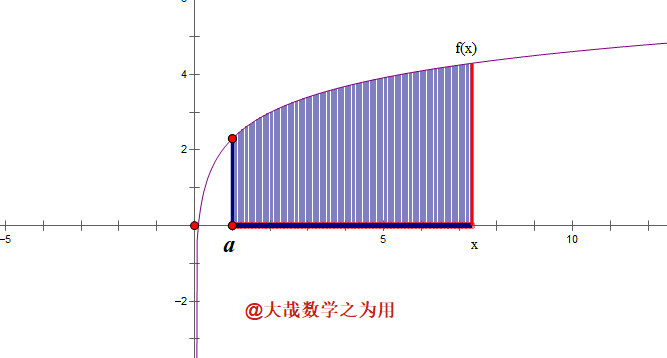
（3）如图3， 物体的速度为任意一个连续函数$y=f(t)$, 从时刻a运动到时刻$x$, 路程可以这样求：将区间$[a,x]$等分成n个小区间，当n充分大时，每个小区间上都可以看成是匀速运动，从而其上的路程为长方形（道理同（1）），整个区间$[a,t]$上的路程为所有这n个长方形的和，让$n\to \infty$，得到$s(x)={\int }_a^{x}f(u)du,$ 它等于曲边梯形的面积，注意还是“面积”。

注意到，牛顿已经知道速度函数$v(x)$是路程函数$s(x)$的“流数”，即今天说的导数，而$s(x)$又是“面积函数”${\int }_a^{x}f(u)du$, 两者联系起来就像拼图一样拼出了下面的公式：
$${\left({\int }_a^{x}f(u)du\right)}^{\prime }=f(x).$$

这个公式说明面积函数$s(x)$是$f(x)$的原函数，反过来说，$f(x)$是$s(x)$的导函数。

02 几何的角度

导数的含义是函数的瞬时变化率。观察下面的动画：曲边梯形可以想像成由函数$f(x)$的纵坐标编织成的。在$x$时刻，比$x$时刻之前所增加的面积正是$f(x)$, 即瞬时变化率等于$f(x)$, 用导数写出来就是下面的公式：
$${\left({\int }_a^{x}f(u)du\right)}^{\prime }=f(x).$$

03 生动的例子

仿照02中的动画，下面的例子可以做类似的解释：将图形的面积或体积看成时间$t$的函数，在$t$时刻编织成面积或体积的“最外层”，则面积函数或体积函数的导数表示$t$时刻增加的面积或体积。

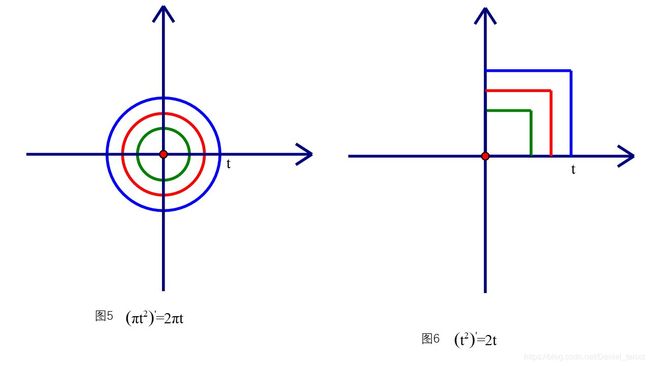
例1 如图5，如果圆的半径在$t$时刻的长度等于$t$, 则$t$时刻时圆的面积为$\pi t^2$. 由于$(\pi t^2{)}^{\prime }=2\pi t$，表明$t$时刻比此时刻之前增加的面积正为$t$时刻时的圆周长$2\pi t.$

例2 如图6，如果正方形的边长在$t$时刻的长度等于$t$, 则$t$时刻时正方形的面积为$t^2$. 由于$(t^2{)}^{\prime }=2t,$ 表明$t$时刻比此时刻之前增加的面积为$2t$，即第一象限的最大的正方形的两个边长。

例3 读者可以自行解释球的体积公式：$V(t{)}^{\prime }=4\pi t^2$的含义。

---

更多内容，欢迎用微信扫描下图中的二维码，或搜索“大哉数学之为用”，免费关注微信公众号“大哉数学之为用”进行阅读。