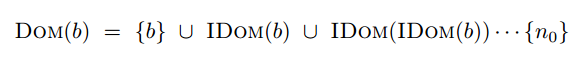构造Dominator Tree以及Dominator Frontier
支配树(Dominator Tree)
在生成SSA的时候,需要计算在何处插入正确的 Φ (phi-function) ,一种方法是在所有有多个前驱的Basic Block的开头插入 Φ-node,但是这种方法会插入很多的无用的 Φ-node ,有很多 Φ-node 的参数都是相同的一个定义。
The Φ-function is the most important SSA concept to grasp. It is a special statement, known as a pseudo-assignment function.
The purpose of a Φ-function is to merge from different incoming paths, at control-flow merge points.
这样得到的 SSA 形式的 IR,占用过多的内存,增加了计算的开销。任何使用该SSA进行代码分析或者优化的过程都会浪费很多计算资源。
这种方法的问题就是得到的SSA形式有太多无用的 Φ-function。为了减少 Φ-function 的数量,首先想到的方法就是确定插入 Φ-function 的精确位置。
It can determine, for each block i, the set of blocks that will need a Φ-function for any definition in block i. Dominance plays a critical role in this computation.
后面我们详细介绍为什么 Dominate 对于决定在何处插入 Φ-function 如此重要,以及如何计算 dominate 信息。
Dominance
如果每一条从流图的入口结点到结点 n 的路径都经过结点 d, 我们就说 d 支配(dominate)n,记为 d dom n。请注意,在这个定义下每个结点都支配它自己。-《编译原理》
d dom i if all paths from entry to node i include d.
上面是龙书中关于支配性的定义,还是比较容易理解的。
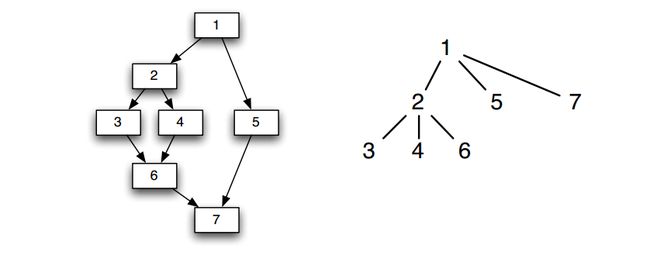
如下图所示:
上面的 flow-graph 入口结点是 1 ,入口结点支配所有结点(这个结论对所有的流图都成立)。结点 2 只能支配它自己,因为控制流可以通过 1 -> 3 开头的路径到达所有其他结点,所以结点 3 支配除 1、2 之外的所有其他结点。
另外一个比较重要的概念就是 strictly dominates(严格支配),如果 d != n 且 d dom n, 那么 d sdom m,例如上图中 4 sdom 5。
Dominator Tree
**The dominator relationship forms a tree. **
Edge from parent to child = parent dominates child.
Note: edges are not same as CFG edges!
支配树(dominator tree)用来表示支配信息,在树中,入口结点,并且每个结点只支配它在树中的后代结点。一种支配树的示例如下:
IDOM ( Immediate dominator )
在支配树(dominator tree)中,对于结点 n 来说,从根节点到结点 n 所在路径上的结点(不包括)都严格支配结点 n,例如上图中从根节点 1 -> 2 -> 3,其中结点 1 和 结点 2 都严格支配结点 3。该路径上离结点 n 最近的结点叫做结点 n 的 直接支配结点(immediate node),用 IDom(n) 表示,例如上图中 IDom(6) = 2。
只要我们能够计算出 IDom 信息,就可以构造出 Dominator Tree。
Dominance Frontier
在构造 SSA 过程中,还有另外一个概念很重要,就是支配边界(dominance frontier)。支配边界直观理解就是当前结点所能支配的边界(并不包括该边界)。
Y is in the dominance frontier of X iff “there exists a path from X to Exit through Y such that Y is the first node not strictly dominated by X”
上面的描述有点绕口,上面的描述也有另一种等价描述“Y 是 X 的支配边界,当且仅当 X 支配 Y 的一个前驱结点(CFG)同时 X 并不严格支配 Y”。
上面的图示直观的表示了支配边界的概念。下面的图给出了一个示例,给出了图中的支配结点以及支配边界关系。
上图中结点 5 支配边界是 4、5、12、13,也就是结点 5 “刚好能力所不能及的地方”。
那么支配边界(dominance frontier)的的意义在哪里呢?
In SSA form, definitions must dominate uses.
下面给出的是wiki中的描述,支配边界确定了 Φ-function 的插入位置。由于每个definition支配对应的uses,所以如果达到了definition所在block的支配边界,就必须考虑其他路径是否有其他相同variable的定义,由于在编译期间无法确定会采用哪一条分支,所以需要放置 Φ-function。
Dominance frontier capture the precise places at which we need Φ-function: if the node A defines a certain variable, then that definition and that definition alone(or redefinitions) will reach every node A dominates.
Only when leave these nodes and enter the diminance frontier must we account for other flows bringing in other definitions of the same variable.
考虑下面的图示, 结点 1 定义了一个值 ***“x := 3”***,这个值可以传播到结点 1 所支配的所有结点(除了 entry 的所有结点)中,只有在到达结点 1 的支配边界的时候,才需要考虑其他路径是否有对 x 的定义并且插入适当的 Φ-function。
虽然从结点 1 的角度来看,在支配结点里面是不需要考虑插入Φ-function的,但是并不保证支配节点(中的join node)中不需要插入 Φ-function。
结点 5 定义了值 ***“x := 4”***,结点 5 没有支配结点并且结点 9 就是结点 5 的支配边界,在这里需要考虑从从其他路径传播到此的对变量 x 的其他定义,也就是结点 1 中的定义 "x := 3" 。所以在结点 9 需要插入一个关于变量 x 的 Φ-function。同理在结点 10 的开头也需要插入一个 Φ-function,另外由于 Φ-function 会产生新的定义,所以也需要在结点 9 的支配边界结点 11 的开头插入 Φ-function。
但是如果要确定支配边界的话,需要先构造出 dominator tree,然后借助于 dominator tree来得出支配边界。
计算支配树
计算支配树最有名的一个算法是 Lengauer-Tarjan algorithm ,这个算法有接近线性的复杂度,但是不是很容易理解(反正我是没有看懂)。当然也有其他方法,例如最简单的方法,就是对于 CFG 中某一个点 A,获取根到结点 A 的一条路径,然后依次删除路径上的某一个点,然后检查结点 A 是否还能从根节点到达。如果删除某个点后,结点 A 从根节点不可达,那么这个点支配结点 A。该方法简单,知道支配性的都会明白该算法,但是该算法复杂度很高,接近 O(N4) 的复杂度。
相比之下,另外一种迭代数据流分析的方法更容易理解,复杂度只有 O(N2) ,几乎现在所有编译方面的书籍都是介绍的这种方法。
《Engineering a Compiler》第9章开篇就是介绍的支配性信息的迭代数据流计算方法,将支配问题看作前向数据流分析,数据流方程如下图(盗图)所示:
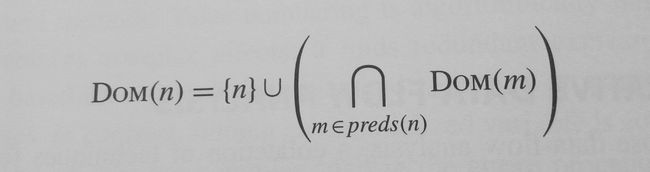
给定初始值,列好数据流方程,迭代到 fixed point 就可以得到支配性信息。
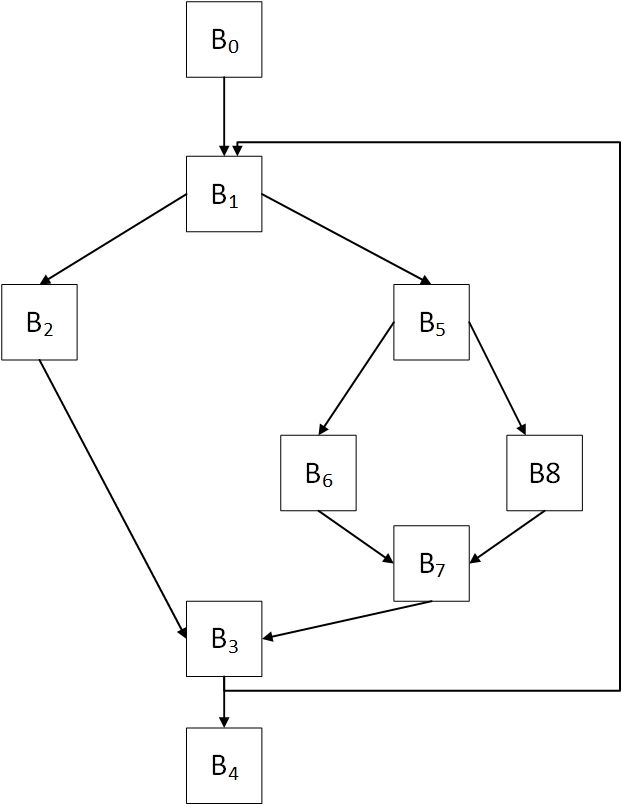
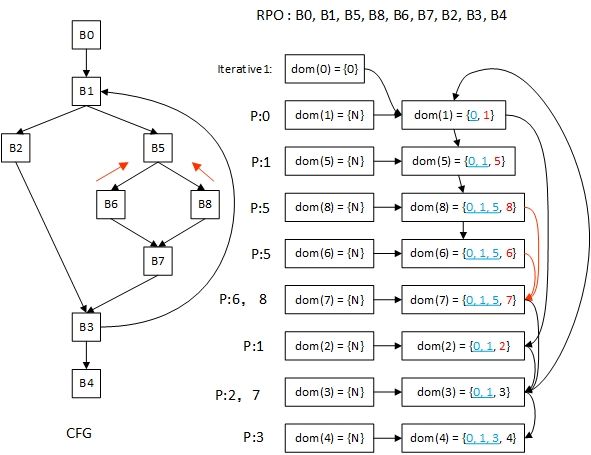
由于是前向数据流问题,所以按照逆后序来进行迭代效率会更高,对应的迭代过程如下图所示:
该方法简单易懂可惜在处理结点个数较多的CFG图时会显得效率有点低,如果想要构造支配树练练手的话,这个方法还是首选。
龙书给出了支配问题的详细描述,如下图(盗图)所示,具体可以去翻看龙书或者《Engineering a Compiler》。该图给出了支配问题的值域,前向数据流问题还是后向数据流问题,传递函数以及交汇运算等等。
A Simple, Fast Dominance Algorithm
这是《Engineering a Compiler》的作者 Cooper 提出的一种算法,该算法在复杂度以及实现难度上作了很好的折中,并且作者生成该算法在实际的 CFG 上的效果与经典的 Lengauer-Tarjan algorithm 相差并不多。
我在自己的习作编译器中使用的也是这个方法,该方法使用框架与经典的迭代方法相同,只是在一些小细节中略有不同。
- 该方法并没有将每个结点的支配结点定义为全集。对于 entry 结点定义 entry,对于其他结点定义为空(undefined)。
- 该方法并不直接计算结点 n 的支配集合***Dom(n)***。而是计算结点 n 的直接支配结点 ***IDom(n)***。
知道了每个结点的 IDom(n) 信息,我们就可以构造出支配树进而计算出支配边界。
经典数据流分析中采用良好的顺序,可以尽快的让数据进行聚合。如果将结点 A 的支配结点集合进行有序排列,那么每一次对结点 A 的前驱结点的聚合(交汇运算),得到的结果就是前驱结点的共同前缀(prefix)。
例如上图中的结点 B7 在第一次迭代时,有两个前驱 B6 和 B8,两者的共同前缀是 “0, 1, 5”,其实只要同时沿着 B6 和 B7向上查找,找到的第一个祖先结点 B5 就可以了,然后我们找到该祖先结点的支配节点集合就是当前结点 B7 的严格支配结点集合。其实这个过程就是寻找当前结点 B7 的 IDom 结点的过程。
上面的过程可以使用一个队列来实现,该队列以结点作为 index,队列中的值为节点的 IDom 结点。例如,在迭代到结点 B7 之前的队列如下所示,我们可以得到结点 B7 的两个前驱 B6 和 B8 的 IDom,如果该 IDom 相同,那么我们该结点就是此次迭代中 B7 的 IDom 结点。因为我们是按照逆后序(前向数据流问题)的顺序迭代的,所以前驱结点 B6 和 B8 的 IDom 结点的 IDom 结点肯定已经计算过了。注:图中的红U表示IDom未定义
在计算完之后,我们从每个结点开始遍历这个队列,遍历所得到的路径就是结点 b 的支配节点集合,通过这些支配结点集合构建出dominator tree。
但是这只是一种想法,中间还有很多细节需要理清楚,比如某个前驱节点的IDom还没有得到。比如使用逆后序第一次迭代到结点 B1 时,B0的前驱结点假设就是B0(B0比较特殊,入口结点),B3的前驱节点还没有得到,此时B3的支配结点集合是全集。此时的Array如下所示:
由于结点 B3 的支配结点集合是全集,而且该数据流分析使用的交汇运算是 “交运算”(描述不是很准确),所以 B0 和 B3 的交汇运算还是 B0,所以在上图中的队列中,在发现某个前驱节点未定义时(也就是全集时)无须考虑该前驱结点,只考虑另外的前驱结点就好了。
Keith D.Cooper 就是基于这个思想提出了一种快速计算 dominance 信息的算法 《A Simple, Fast Dominance Algorithm》。该算法简单易懂,效果也不错,算法伪代码如下所示:
算法中的 doms[b] 表示的就是上面介绍的队列,intersect(b1, b2)函数实现的就是找这两个前驱的在DomTree中最近公共祖先的方法(实现的是传统迭代数据流分析两个支配集合做交汇运算)。框架使用的还是传统的迭代数据流分析的框架,只是求解的不是 DomSet, 而是IDom信息,并且必须使用逆后序来进行迭代。
下图是这篇论文中给出的示例,具体过程我就不详述了,感兴趣的去翻论文。
计算支配边界(dominance frontier)
Cooper在这篇论文中也提出了一种改进的计算支配边界的方法(改进很小),该算法如下所示:
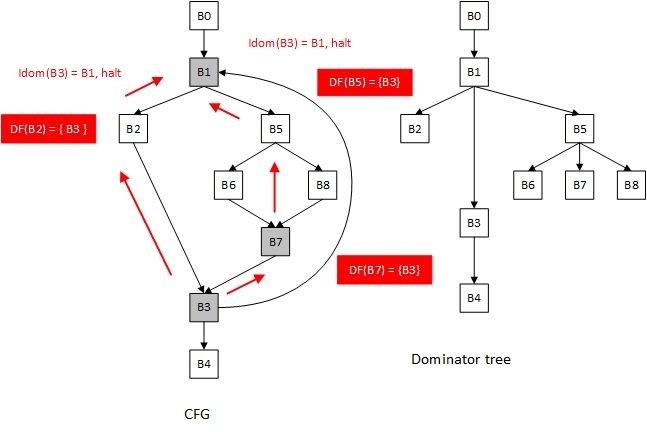
只要得到了 dominance 信息,计算 dominance frontier 就很简单了。我们用下面的图来简单分析一下该算法的实现。
计算支配边界的算法第一步就是遍历所有结点,然后找到有多个前驱的结点(也就是***join node***),上面这张图给出了在遍历到结点 B3 时的状态,图中灰色结点表示有多个前驱的结点。
按照算法描述,我们需要遍历结点 B3 的两个前驱 B2 和 B7,在遍历到 B2 时,B2 不是 B3 的 IDom 结点,则将 B3 加入到结点 B2 的支配边界集合中。然后将 runner 更新为 B2 的 IDom 结点 B1,由于 B1 是结点 B3 的 IDom 结点,所以这条路径向上的遍历跳出 while 循环。同理,在遍历前驱结点 B7 这条路径时,同样会将 B3 加入到 B7 以及 B5 的支配边界集合中,知道遍历到 B1 跳出 while 循环。
其实该算法还有改进的地方,就是在外层循环中,只遍历有多个前驱的结点,这些信息在计算支配信息的时候就可以顺手得到,只是这个改进需要额外的空间来存储有多个前驱的结点集合。
实现代码
class DomTreeNode
{
public:
enum class color {WHITE, GRAY, BLACK};
private:
BBPtr TheBB;
int PostNumber;
int DFSInNum, DFSOutNum;
color VisitColor;
DomTreeNodePtr IDom;
std::vector Children;
// Express the predecessor when we depth-first searching of
// the CFG.
// e.g.
// B1 B2
// \ /
// \ /
// B3
// B1 and B2 both the father of B3, but we only can via one
// node reach B3 when the depth-first searching.
DomTreeNodePtr Father;
public:
DomTreeNode(BBPtr BB = nullptr) :
TheBB(BB), IDom(nullptr), DFSInNum(-1), DFSOutNum(-1),
PostNumber(-1), Father(nullptr) {}
BBPtr getBlock() const { return TheBB; }
DomTreeNodePtr getIDom() const { return IDom; }
const std::vector& getChildren() const
{
return Children;
}
DomTreeNodePtr addChild(DomTreeNodePtr Child)
{
Children.push_back(Child);
return Child;
}
std::vector Predecessors;
unsigned getDFSNumIn() const { return DFSInNum; }
unsigned getDFSNumOut() const { return DFSOutNum; }
unsigned getPostOrder() const { return PostNumber; }
bool DominatedBy(DomTreeNodePtr other) const
{
return this->DFSInNum >= other->DFSInNum &&
this->DFSOutNum <= other->DFSOutNum;
}
void setDFSInNum(int InNum) { DFSInNum = InNum; }
void setDFSOutNum(int OutNum) { DFSOutNum = OutNum; }
void setPostNumber(int PostOrder) { PostNumber = PostOrder; }
void setVisitColor(color c) { VisitColor = c; }
void setDFSFather(DomTreeNodePtr DFSFather) { Father = DFSFather; }
color getVisitColor() const { return VisitColor; }
size_t getNumChildren() const { return Children.size(); }
void clearAllChildren() { Children.clear(); }
void setIDom(DomTreeNodePtr NewIDom)
{
IDom = NewIDom;
}
};
//===------------------------------------------------------------===//
// A dominator tree is a tree where each node's children are those
// nodes it immediately dominates.
// Because the immediate dominator is unique, it is a tree. The start
// node is the root of the tree.
// DominatorTree - This represents the forward Dominance.
class DominatorTree
{
using DomTreeNodeMapType = std::map;
DomTreeNodeMapType DomTreeNodes;
DomTreeNodePtr RootNode;
std::vector PostOrder;
std::vector ReversePostOrder;
std::list Vertex;
std::map> PredecessorrsOfCFG;
// DominanceFrontier - Represent the forward Dominance Frontier.
std::map> DominanceFrontier;
// JoinPoints - Represent the join point(have more than two predecessors)
// of CFG.
std::vector JoinNodes;
private:
void getPostOrder();
void getReversePostOrder();
// compute the DomTree.
void computeDomTree(BBPtr EntryBlock);
// 获取当前DomNode在CFG中前驱对应的DomTreeNode.
std::vector getDomNodePredsFromCFG(DomTreeNodePtr Node);
// Intersect() - This function only be using to get closest parent of A and B.
DomTreeNodePtr Intersect(DomTreeNodePtr A, DomTreeNodePtr B);
// Insert the frontier.
void InsertFrontier(DomTreeNodePtr Node, DomTreeNodePtr FrontierItem);
// ComputeDomFrontier() - Compute the forward dominance frontier.
void ComputeDomFrontier();
public:
// compute the DomTree of the CFG.
void runOnCFG(std::vector &BBs);
// compute the DomTree of the Function.
void runOnFunction(FuncPtr F);
void ComputeDomFrontierOnCFG(std::vector &BBs);
void ComputeDomFrontierOnFunction(FuncPtr F);
DomTreeNodePtr getDomTreeNode(BBPtr BB) const;
// getRootNode - This returns the entry node for the CFG of the function.
DomTreeNodePtr getRootNode() { return RootNode; }
bool properlyDominates(DomTreeNodePtr Node) const;
bool isReachableFromEntry(BBPtr BB) const;
bool dominates(DomTreeNodePtr A, DomTreeNodePtr B) const;
// printIDoms - Convert IDoms to human readable form.
void printIDoms(std::ostream &out) const;
// printDF - Convert Dom Frontier to human readable form.
void printDomFrontier(std::ostream &out) const;
void DFS(DomTreeNodePtr Node);
// Calcuate - compute a dominator tree for the given function.
void Calcuate();
// dominates - Return true if A dominates B. This perform the special
// checks necessary if A and B are in the same basic block.
bool dominates(InstPtr A, InstPtr B) const;
};
上面的代码是 DomTreeNode 以及 DominatorTree 的来定义。
我们使用类 DomTreeNode 来包裹 BasicBlock,其中比较重要有 IDom 数据成员用来表示当前结点的直接支配结点,另外还有一些辅助深度优先遍历的数据成员。我们通过深度优先遍历确定 CFG 的后序以及逆后序。
我们使用类 DominatorTree 来表示支配树,其中 DomTreeNodes 用来表示进行迭代数据流分析时的列表,DominanceFrontier 表示每个结点的支配边界集合,PredecessorrsOfCFG 表示结点在 CFG 中的前驱结点。我们使用 runOnCFG() 和 runOnFunction() 来计算支配树(其实并没有真正构造一棵树出来,只是维护了支配信息)。ComputeDomFrontierOnCFG() 和 ComputeDomFrontierOnFunction() 用来计算支配边界。
void DominatorTree::Calcuate()
{
if (ReversePostOrder.size() == 0)
getReversePostOrder();
// iterate
bool changed = true;
RootNode->setIDom(RootNode);
while (changed)
{
changed = false;
for (auto CurNode : ReversePostOrder)
{
if (CurNode == RootNode)
continue;
// Get the predecessors of current node.
auto PredDomNodeFromCFG = getDomNodePredsFromCFG(CurNode);
// (1) Find the first non-nullptr predecessor.
auto getAvailiablePred =
[this, &PredDomNodeFromCFG]() -> DomTreeNodePtr
{
// 从Preds中找到一个IDom不为空的predecessor.
for (auto pred : PredDomNodeFromCFG)
{
if (pred->getIDom() != nullptr)
return pred;
}
assert(0 && "Unreachable code.");
return nullptr;
};
auto AvailiablePred = getAvailiablePred();
DomTreeNodePtr NewIDom = AvailiablePred;
// (2) Traverse other predecessors.
for (auto pred : PredDomNodeFromCFG)
{
if (pred == NewIDom)
continue;
if (pred->getIDom() != nullptr)
NewIDom = Intersect(NewIDom, pred);
}
// (3) Judge the IDom is changed.
if (CurNode->getIDom() != NewIDom)
{
CurNode->setIDom(NewIDom);
changed = false;
}
}
}
}
void DominatorTree::ComputeDomFrontier()
{
DomTreeNodePtr runner = nullptr;
// Just compute the join points.
for (auto Node : JoinNodes)
{
auto preds = getDomNodePredsFromCFG(Node);
for (auto pred : preds)
{
runner = pred;
while (runner != Node->getIDom())
{
InsertFrontier(runner, Node);
runner = runner->getIDom();
}
}
}
}
上面的 Calculate() 和 ComputeDomFrontier() 分别用来计算支配信息和支配边界的函数,函数几乎是按照 Cooper 的论文实现的,很简单我就不详述了。
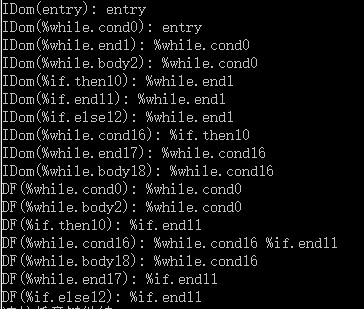
使用很简单的代码进行验证:
//---------------------示例代码--------------------------
var number = 100;
var sum : int;
while(number > 0)
{
sum += number--;
}
var result : bool;
if (sum > 100000)
{
result = true;
while(sum > 0)
{
sum--;
}
}
else
{
result = false;
}
// ----------------------渣到爆的IR---------------------
entry:
%number.addr = alloca int ; < int* >
%sum.addr = alloca int ; < int* >
%result.addr = alloca bool ; < bool* >
store int 100.000000, int* %number.addr ; < void >
br label %while.cond0
%while.cond0:
%3 = load int* %number.addr ; < int >
%gt.result4 = cmp gt int %3, int 0.000000 ; < bool >
br bool %gt.result4, label %while.body2, label %while.end1
%while.body2:
%5 = load int* %number.addr ; < int >
%dec6 = add int %5, int -1 ; < int >
store int %dec6, int* %number.addr ; < void >
%7 = load int* %sum.addr ; < int >
%add.tmp8 = add int %7, int %5 ; < int >
store int %add.tmp8, int* %sum.addr ; < void >
%9 = load int* %sum.addr ; < int >
br label %while.cond0
%while.end1:
%13 = load int* %sum.addr ; < int >
%gt.result14 = cmp gt int %13, int 100000.000000 ; < bool >
br bool %gt.result14, label %if.then10, label %if.else12
%if.then10:
store bool , bool* %result.addr ; < void >
%15 = load bool* %result.addr ; < bool >
br label %while.cond16
%while.cond16:
%19 = load int* %sum.addr ; < int >
%gt.result20 = cmp gt int %19, int 0.000000 ; < bool >
br bool %gt.result20, label %while.body18, label %while.end17
%while.body18:
%21 = load int* %sum.addr ; < int >
%dec22 = add int %21, int -1 ; < int >
store int %dec22, int* %sum.addr ; < void >
br label %while.cond16
%while.end17:
br label %if.end11
%if.else12:
store bool , bool* %result.addr ; < void >
%23 = load bool* %result.addr ; < bool >
br label %if.end11
%if.end11: