【NLP】隐马尔可夫模型三个基本问题相关算法实现

前言

  隐马尔可夫模型详解，本篇详细介绍了隐马尔可夫模型的相关理论知识，为了进一步的理解它，本篇将通过具体的计算例子，通过代码实现解决三个基本问题的算法，前向-后向算法、Baum-Welch算法、Viterbi算法。

• 概率计算问题：前向-后向算法

  给定模型 $\lambda =(A,B,\pi )$ 和观测序列 $Q=\{q_1,q_2,...,q_T\}$，计算模型 $\lambda$ 下观测到序列Q出现的概率 $P(Q|\lambda )$

• 学习问题：Baum-Welch算法(状态未知)

  已知观测序列 $Q=\{q_1,q_2,...,q_T\}$，估计模型 $\lambda =(A,B,\pi )$ 的参数，使得在该模型下观测序列 $P(Q|\lambda )$ 最大。

• 预测问题：Viterbi算法

  给定模型 $\lambda =(A,B,\pi )$ 和观测序列 $Q=\{q_1,q_2,...,q_T\}$，求给定观测序列条件概率 $P(I|Q，\lambda )$ 最大的状态序列 $I$

理论部分内容可参考 隐马尔可夫模型详解，本篇不再重复叙述。

本篇代码可见：Github

一、案例描述

  假设有三个盒子，编号为 $1,2,3$ ；每个盒子都装有黑白两种颜色的小球，球的比例如下：

编号	白球	黑球
1	4	6
2	8	2
3	5	5

  按照下列规则的方式进行有放回的抽取小球，得到球颜色的观测序列：

• 按照 $\pi$ 的概率选择一个盒子，从盒子中随机抽取出一个小球，记录颜色后，放回盒子中；
• 按照某种条件概率选择新的盒子，重复该操作；
• 最终得到观测序列：“白黑白白黑”

该问题中的变量定义：

• 状态集合：$S=\{盒子1，盒子2，盒子3\}$
• 观测集合：$O=\{白，黑\}$
• 状态序列和观测序列的长度 $T=5$
• 初始概率分布 $\pi$

$$\pi =(0.2,0.5,0.3{)}^T$$

• 状态转移概率矩阵 $A$

$$A=\left[\begin{array}{ccc}0.5& 0.4& 0.1\\ 0.2& 0.2& 0.6\\ 0.2& 0.5& 0.3\end{array}\right]$$

• 观测概率矩阵 $B$

$$B=\left[\begin{array}{cc}0.4& 0.6\\ 0.8& 0.2\\ 0.5& 0.5\end{array}\right]$$

在给定参数 $\pi 、A、B$ 的时候，得到观测序列 $Y=\{白,黑,白,白,黑\}$ 的概率是多少?

二、概率计算问题

2.1 前向算法

前向算法描述如下：

输入：隐马尔可夫模型$\lambda$，观测序列 $Y$

输出：观测序列概率$P(Y|\lambda )$

（1）初值
$${\alpha }_1(i)={\pi }_i{b}_i(y_1)，i=1,2,..,N$$
（2）递推 \quad 对$t=1,2,...,T-1$
$${\alpha }_{t+1}(i)=[\sum _{j=1}^N{\alpha }_t(j)a_{ij}]b_i(y_{t+1})，i=1,2,...,N$$
（3）终止
$$p(Y|\lambda )=\sum _{i=1}^N{\alpha }_T(i)$$

手动计算：

（1）初值

$${\alpha }_1(1)={\pi }_1{b}_1(y_1)=0.2\times 0.4=0.08$$
$${\alpha }_1(2)={\pi }_2{b}_2(y_1)=0.5\times 0.8=0.40$$
$${\alpha }_1(2)={\pi }_3{b}_3(y_1)=0.3\times 0.5=0.15$$

（2）递推

$$\begin{gathered} {\alpha }_2(1)=(\sum _{j=1}^3{\alpha }_1(j)a_{j1})b_1(y_2)=(0.08\times 0.5+0.4\times 0.2+0.15\times 0.2)\times 0.6=0.09 \\ {\alpha }_2(2)=(\sum _{j=1}^3{\alpha }_1(j)a_{j2})b_2(y_2)=(0.08\times 0.4+0.4\times 0.2+0.15\times 0.5)\times 0.2=0.0374 \\ {\alpha }_2(3)=(\sum _{j=1}^3{\alpha }_1(j)a_{j3})b_3(y_2)=(0.08\times 0.1+0.4\times 0.6+0.15\times 0.3)\times 0.5=0.1465 \end{gathered}$$

---

$$\begin{gathered} {\alpha }_3(1)=(\sum _{j=1}^3{\alpha }_2(j)a_{j1})b_1(y_3)=(0.09\times 0.5+0.0374\times 0.2+0.1465\times 0.2)\times 0.4=0.032712 \\ {\alpha }_3(2)=(\sum _{j=1}^3{\alpha }_2(j)a_{j2})b_2(y_3)=(0.09\times 0.4+0.0374\times 0.2+0.1465\times 0.5)\times 0.8=0.093384 \\ {\alpha }_3(3)=(\sum _{j=1}^3{\alpha }_2(j)a_{j3})b_3(y_3)=(0.09\times 0.1+0.0374\times 0.6+0.1465\times 0.3)\times 0.5=0.037695 \end{gathered}$$

---

$$\begin{gathered} {\alpha }_4(1)=(\sum _{j=1}^3{\alpha }_2(j)a_{j1})b_1(y_4)=(0.032712\times 0.5+0.093384\times 0.2+0.037695\times 0.2)\times 0.4=0.01702872 \\ {\alpha }_4(2)=(\sum _{j=1}^3{\alpha }_2(j)a_{j2})b_2(y_4)=(0.032712\times 0.4+0.093384\times 0.2+0.037695\times 0.5)\times 0.8=0.04048728 \\ {\alpha }_4(3)=(\sum _{j=1}^3{\alpha }_2(j)a_{j3})b_3(y_4)=(0.032712\times 0.1+0.093384\times 0.6+0.037695\times 0.3)\times 0.5=0.03530505 \end{gathered}$$

---

$$\begin{gathered} {\alpha }_5(1)=(\sum _{j=1}^3{\alpha }_2(j)a_{j1})b_1(y_5)=(0.01702872\times 0.5+0.04048728\times 0.2+0.03530505\times 0.2)\times 0.6=0.0142036956 \\ {\alpha }_5(2)=(\sum _{j=1}^3{\alpha }_2(j)a_{j2})b_2(y_5)=(0.01702872\times 0.4+0.04048728\times 0.2+0.03530505\times 0.5)\times 0.2=0.0065122938 \\ {\alpha }_5(3)=(\sum _{j=1}^3{\alpha }_2(j)a_{j3})b_3(y_5)=(0.01702872\times 0.1+0.04048728\times 0.6+0.03530505\times 0.3)\times 0.5=0.0182933775 \end{gathered}$$

（3）终止

$$p(Y|\lambda )=\sum _{i=1}^3{\alpha }_5(i)=0.0142036956+0.0065122938+0.0182933775=0.0390093669$$

程序运行结果：

上图中，$\alpha$ 矩阵中每行表示 ${\alpha }_T(i)$
通过比较我们手算的和程序的运行结果，我们发现他们的结果是一样的（忽略精度问题）
程序中有注释，具体内容可查看源代码

代码可见：hmm01/forward_probability.py

2.2 后向算法

后向算法描述如下：

输入：隐马尔可夫模型$\lambda$，观测序列 $Y$

输出：观测序列概率$P(Y|\lambda )$

（1）初值
$${\beta }_T(i)=1，i=1,2,..,N$$
（2）递推 \quad 对$t=T-1,T-2,...,1$
$${\beta }_t(i)=\sum _{j=1}^N{a}_{ij}{b}_j(y_{t+1}){\beta }_{t+1}(j)，i=1,2,...,N$$
（3）终止
$$p(Y|\lambda )=\sum _{i=1}^N{\pi }_i{b}_i(y_1){\beta }_1(i)$$

手动计算：

（1）初值

$$\begin{gathered} {\beta }_5(1)=1 \\ {\beta }_5(2)=1 \\ {\beta }_5(3)=1 \end{gathered}$$

（2）递推

$$\begin{gathered} {\beta }_4(1)=\sum _{j=1}^3{a}_{1j}{b}_j(y_5){\beta }_5(j)=0.5\times 0.6\times 1+0.4\times 0.2\times 1+0.1\times 0.5\times 1=0.43 \\ {\beta }_4(2)=\sum _{j=1}^3{a}_{2j}{b}_j(y_5){\beta }_5(j)=0.2\times 0.6\times 1+0.2\times 0.2\times 1+0.6\times 0.5\times 1=0.46 \\ {\beta }_4(3)=\sum _{j=1}^3{a}_{3j}{b}_j(y_5){\beta }_5(j)=0.2\times 0.6\times 1+0.5\times 0.2\times 1+0.3\times 0.5\times 1=0.37 \end{gathered}$$

---

$$\begin{gathered} {\beta }_3(1)=\sum _{j=1}^3{a}_{1j}{b}_j(y_4){\beta }_4(j)=0.5\times 0.4\times 0.43+0.4\times 0.8\times 0.46+0.1\times 0.5\times 0.37=0.2517 \\ {\beta }_3(2)=\sum _{j=1}^3{a}_{2j}{b}_j(y_4){\beta }_4(j)=0.2\times 0.4\times 0.43+0.2\times 0.8\times 0.46+0.6\times 0.5\times 0.37=0.219 \\ {\beta }_3(3)=\sum _{j=1}^3{a}_{3j}{b}_j(y_4){\beta }_4(j)=0.2\times 0.4\times 0.43+0.5\times 0.8\times 0.46+0.3\times 0.5\times 0.37=0.2739 \end{gathered}$$

---

$$\begin{gathered} {\beta }_2(1)=\sum _{j=1}^3{a}_{1j}{b}_j(y_3){\beta }_3(j)=0.5\times 0.4\times 0.2517+0.4\times 0.8\times 0.219+0.1\times 0.5\times 0.2739=0.134115 \\ {\beta }_2(2)=\sum _{j=1}^3{a}_{2j}{b}_j(y_3){\beta }_3(j)=0.2\times 0.4\times 0.2517+0.2\times 0.8\times 0.219+0.6\times 0.5\times 0.2739=0.137346 \\ {\beta }_2(3)=\sum _{j=1}^3{a}_{3j}{b}_j(y_3){\beta }_3(j)=0.2\times 0.4\times 0.2517+0.5\times 0.8\times 0.219+0.3\times 0.5\times 0.2739=0.148821 \end{gathered}$$

---

$$\begin{gathered} {\beta }_1(1)=\sum _{j=1}^3{a}_{1j}{b}_j(y_2){\beta }_2(j)=0.5\times 0.6\times 0.134115+0.4\times 0.2\times 0.137346+0.1\times 0.5\times 0.148821=0.05866323 \\ {\beta }_1(2)=\sum _{j=1}^3{a}_{2j}{b}_j(y_2){\beta }_2(j)=0.2\times 0.6\times 0.134115+0.2\times 0.2\times 0.137346+0.6\times 0.5\times 0.148821=0.06623394 \\ {\beta }_1(3)=\sum _{j=1}^3{a}_{3j}{b}_j(y_2){\beta }_2(j)=0.2\times 0.6\times 0.134115+0.5\times 0.2\times 0.137346+0.3\times 0.5\times 0.148821=0.05215155 \end{gathered}$$

（3）终止

$$p(Y|\lambda )=\sum _{i=1}^3{\pi }_i{b}_i(y_1){\beta }_1(i)=0.2\times 0.4\times 0.05866323+0.5\times 0.8\times 0.06623394+0.3\times 0.5\times 0.05215155=0.0390093669$$

程序运行结果：

得到的结果和前向算法一样，具体内容可参考源代码注释

代码可见：hmm01/backward_probability.py

三、学习问题

Baum-Welch算法描述如下：

输入：观测数据$Y=(y_1,y_2,...,y_T)$

输出：隐马尔可夫模型参数

（1）初始化

对$n=0$，选取$a_{ij}^{(0)},{b_j(k)}^{(0)},{\pi }_i^{(0)}$，得到模型${\lambda }^{(0)}=(A^{(0)},B^{(0)},{\pi }^{(0)})$

（2）递推，对$n=1,2,...,$
$$a_{ij}^{(n+1)}=\frac{{\sum }_{t=1}^{T-1}P(Y,i_t=i,i_{t+1}=j|\overline{\lambda })}{{\sum }_{t=1}^{T-1}P(Y,i_t=i,|\overline{\lambda })}$$

$$b_j(k{)}^{(n+1)}=\frac{{\sum }_{t=1}^{T}P(Y,i_t=j|\overline{\lambda })I(y_t=v_k)}{{\sum }_{t=1}^{T}P(Y,i_t=j|\overline{\lambda })}$$

$${\pi }_i^{(n+1)}=\frac{P(Y,i_1=i|\overline{\lambda })}{{\sum }_{i=1}^{N}P(Y,i_1=i|\overline{\lambda })}$$

右端各值按模型${\lambda }^{(n)}=(A^{(n)},B^{(n)},{\pi }^{(n)})$计算

（3）终止。得到模型参数${\lambda }^{(n+1)}=(A^{(n+1)},B^{(n+1)},{\pi }^{(n+1)})$

利用前向和后向概率对Baum-Welch算法中的表达式进行修改：

• 给定模型 $\lambda$ 和观测序列 $Y$，在时刻 $t$ 处于状态 $q_i$ 的概率，记为：

$${\gamma }_t(i)=P(i_t=q_i|Y,\lambda )=\frac{P(i_t=q_i,Y|\lambda )}{P(Y|\lambda )}=\frac{{\alpha }_t(i){\beta }_t(i)}{{\sum }_{j=1}^N{\alpha }_t(j){\beta }_t(j)}$$

其中：
$${\alpha }_t(i){\beta }_t(i)=P(i_t=q_i,Y|\lambda )$$

def calc_gamma(alpha, beta, gamma):
    """
    根据alphe和beta的值计算gamma值
    最终结果保存在gamma矩阵中
    """
    T = len(alpha)
    n_range = range(len(alpha[0]))
    tmp = [0 for i in n_range]
    for t in range(T):
        # 累加t时刻对应的所有状态值的前向概率和后向概率，从而计算分母
        for i in n_range:
            tmp[i] = alpha[t][i] * beta[t][i]
        sum_alpha_beta_of_t = np.sum(tmp)

        # 更新gamma值
        for i in n_range:
            gamma[t][i] = tmp[i] / sum_alpha_beta_of_t

• 给定模型 $\lambda$ 和观测序列 $Y$，在时刻 $t$ 处于状态 $q_i$ 且在时刻 $t+1$ 处于 $q_j$ 的概率，记为：

$${\xi }_t(i,j)=P(i_t=q_i,i_{t+1}=q_j|Y,\lambda )=\frac{P(i_t=q_i,i_{t+1}=q_j,Y|\lambda )}{P(Y|\lambda )}$$
$$=\frac{P(i_t=q_i,i_{t+1}=q_j,Y|\lambda )}{{\sum }_{i=1}^N{\sum }_{j=1}^{N}P(i_t=q_i,i_{t+1}=q_j,Y|\lambda )}$$
$$=\frac{{\alpha }_t(i)a_{ij}{b}_j(y_{t+1}){\beta }_{t+1}(j)}{{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_t(i)a_{ij}{b}_j(y_{t+1}){\beta }_{t+1}(j)}$$

其中：
$$P(i_t=q_i,i_{t+1}=q_j,Y|\lambda )={\alpha }_t(i)a_{ij}{b}_j(y_{t+1}){\beta }_{t+1}(j)$$
以上，${\alpha }_t(i),{\beta }_t(i)$分别表示前向和后向概率

def calc_ksi(alpha, beta, A, B, Q, ksi, fetch_index_by_obs_seq=None):
    """
    计算时刻t的时候状态为i，时刻t+1的时候状态为j的联合概率ksi
    alpha：对应的前向概率值
    beta：对应的后向概率值
    A：状态转移矩阵
    B: 状态和观测值之间的转移矩阵
    Q: 观测值列表
    ksi：待求解的ksi矩阵
    fetch_index_by_obs_seq: 根据序列获取对应索引值的函数，可以为空
    NOTE:
        1. ord函数的含义是将一个单个的字符转换为数字, eg: ord('a') = 97; ord('中')=20013；底层其实是将字符转换为ASCII码；
        2. 最终会直接更新参数中的ksi矩阵
    """
    # 0. 初始化
    # 初始化序列转换为索引的方法
    fetch_index_by_obs_seq_f = fetch_index_by_obs_seq
    if fetch_index_by_obs_seq_f is None:
        fetch_index_by_obs_seq_f = lambda obs, obs_index: ord(obs[obs_index])

    # 初始化相关的参数值: n、T
    T = len(alpha)
    n = len(A)

    # 1. 开始迭代更新
    n_range = range(n)
    tmp = np.zeros((n, n))

    for t in range(T - 1):
        # 1. 计算t时刻状态为i，t+1时刻状态为j的概率值
        for i in n_range:
            for j in n_range:
                tmp[i][j] = alpha[t][i] * A[i][j] * B[j][fetch_index_by_obs_seq_f(Q, t + 1)] * beta[t + 1][j]

        # 2. 计算t时候的联合概率和
        sum_pro_of_t = np.sum(tmp)

        # 2. 计算时刻t时候的联合概率ksi
        for i in n_range:
            for j in n_range:
                ksi[t][i][j] = tmp[i][j] / sum_pro_of_t

修改算法中第二步：递推

$$a_{ij}^{(n+1)}=\frac{{\sum }_{t=1}^{T-1}{\xi }_t(i,j)}{{\sum }_{t=1}^{T-1}{\gamma }_t(i)}$$
$${b_j(k)}^{(n+1)}=\frac{{\sum }_{t=1,y_t=v_k}^T{\gamma }_t(j)}{{\sum }_{t=1}^T{\gamma }_t(j)}$$
$${\pi }_t^{(n+1)}={\gamma }_t(i)$$

代码中，我们首先计算了$\gamma ，\xi$的值，然后使用该值代入Baum-Welch算法中。

计算 $\gamma$ 的运行结果：

可见代码：hmm01/single_state_probability_of_gamma.py

计算 $\xi$ 的运行结果：

可见代码：hmm01/continuous_state_probability_of_ksi.py

Baum-Welch算法实现：

代码可见：hmm01/baum_welch.py

四、预测问题

维特比算法描述如下：

输入：模型 $\lambda =(A,B,\pi )$ 和观测 $O=(o_1,o_2,...,o_T)$；

输出：最优路径 $I^{\ast }=(i_1^{\ast },i_2^{\ast },...,i_T^{\ast })$；

（1）初始化

$${\delta }_1(i)={\pi }_i{b}_i(o_1),i=1,2,...,N$$
$${\psi }_1(i)=0,i=1,2,..,N$$

（2）递推，对 $t=2,3,...,T$

$${\delta }_t(i)=\underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)a_{ji}]b_i(o_t),i=1,2,...,N$$
$${\psi }_t(i)=arg\underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)a_{ji}],i=1,2,...,N$$

（3）终止

$$P^{\ast }=\underset{1\le i\le N}{\max }{\delta }_T(i)$$
$$i_T^{\ast }=arg\underset{1\le i\le N}{\max }[{\delta }_T(i)]$$

（4）最优路径回溯，对 $t=T-1,T-2,...,1$

$$i_t^{\ast }={\psi }_{t+1}(i_{t+1}^{\ast })$$

求得最优路径 $I^{\ast }=(i_1^{\ast },i_2^{\ast },...,i_T^{\ast })$

实例计算可参考：隐马尔可夫模型详解中对应部分的实例。而程序中的 $A,B,\pi$ 是我们设置的，实际应用中 $A,B,\pi$ 是根据学习算法得到的最优模型进行预测

维特比算法运行结果：

代码可见：hmm01/viterbi.py

五、改进版本

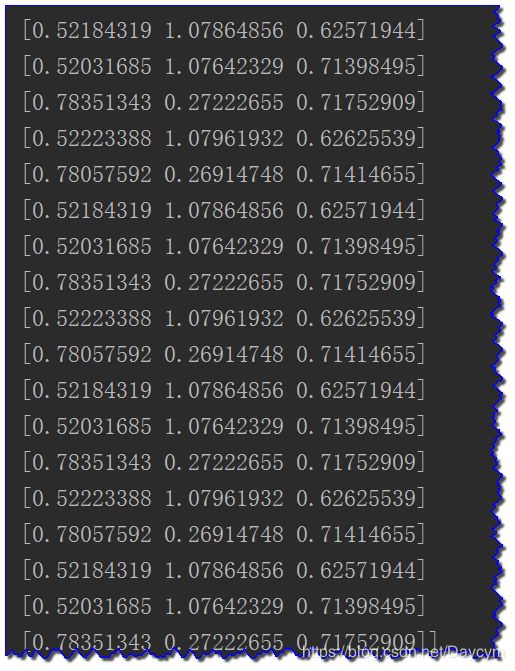
在计算相关概率的时候，如果我们的观测序列比较长，程序前向概率结果如下（只截取了后面一部分）：

图中我们可以看出，随着观测序列增加，前向概率在逐渐减少趋向于0，因此很有可能造成溢出，我们需要对此进行一定的改进。

我们只需要对之前的求得的值进行 log_sum_exp 操作即可

def log_sum_exp(a):
    """
    可以参考numpy中的log sum exp的API
    scipy.misc.logsumexp
    :param a:
    :return:
    """
    a = np.asarray(a)
    a_max = max(a)
    tmp = 0
    for k in a:
        tmp += math.exp(k - a_max)
    return a_max + math.log(tmp)

修改后运行结果：

有上图可见，值都在0-1之间

改版后的代码可见：hmm02/common.py 和 hmm02/hmm_learn.py

六、应用（分词）

  本节我们就使用上面的 hmm02/common.py 和 hmm02/hmm_learn.py 来训练分词用的HMM，大体可分为如下步骤：

• 训练数据的获取（这里使用的pku_training.utf8）
• 读取上面的训练数据到模型训练（加载数据、初始化$(\pi ,A,B)$、模型训练、返回结果）
• 模型的保存
• 模型加载
• 应用模型分词

看上去分词效果还有点样子，好像有那么些回事，当然要想分词效果好，自然需要更多的词库。
具体内容可见代码注释部分

代码可见：hmm02/split_word_with_hmm.py

七、总结

  我相信通过代码的理解，我们更能对理论部分的一些公式进一步的理解，而且代码也是根据公式写出来的。具体的内容需各自查看代码及注释。

  一开始，我们是直接根据公式来写的，后来发现在观测序列越长的情况下，概率会越趋向于0，然后我们做了log_sum_exp ，其实代码底层也加了这个。