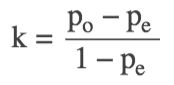kappa系数在评测中的应用
◆版权声明:本文出自胖喵~的博客,转载必须注明出处。
转载请注明出处:http://www.cnblogs.com/by-dream/p/7091315.html
前言
最近打算把翻译质量的人工评测好好的做一做。
首先废话几句,介绍下我这边翻译质量的人工评测怎么做。先找一批句子,然后使用不同的引擎对其进行翻译,然后将原文和译文用下面的方式进行呈现,把这些交给专业的人士去进行打分,打完分之后,对结果进行统计,得出评测结果。
看似流程很顺利,且结果也有参考价值。然而实际操作的过程中发现如果一个用户的能力或者态度有问题的话,就会影响一个打分的效果。因此评测人员究竟是否靠谱也成了我们需要考虑的一项因素。
通过向专业人士请教,得知了kappa系数可以进行一致性的校验且可用来衡量分类精度。因此我决定试试它。
好了先看看kappa系数的概念和计算公式。
kappa系数概念
它是通过把所有地表真实分类中的像元总数(N)乘以混淆矩阵对角线(Xkk)的和,再减去某一类地表真实像元总数与被误分成该类像元总数之积对所有类别求和的结果,再除以总像元数的平方减去某一类中地表真实像元总数与该类中被误分成该类像元总数之积对所有类别求和的结果所得到的。
——来自百科
kappa计算结果为-1~1,但通常kappa是落在 0~1 间,可分为五组来表示不同级别的一致性:0.0~0.20极低的一致性(slight)、0.21~0.40一般的一致性(fair)、0.41~0.60 中等的一致性(moderate)、0.61~0.80 高度的一致性(substantial)和0.81~1几乎完全一致(almost perfect)。
计算公式:
po是每一类正确分类的样本数量之和除以总样本数,也就是总体分类精度
假设每一类的真实样本个数分别为a1,a2,...,aC
而预测出来的每一类的样本个数分别为b1,b2,...,bC
总样本个数为n
则有:pe=a1×b1+a2×b2+...+aC×bC / n×n
运算举例
为了更好的理解上述运算的过程,这里举例说明一下:
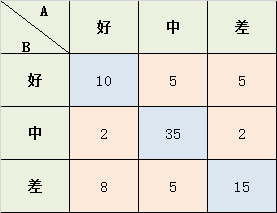
学生考试的作文成绩,由两个老师给出 好、中、差三档的打分,现在已知两位老师的打分结果,需要计算两位老师打分之间的相关性kappa系数:
a1 = 10+2+8 = 20; a2 = 5+35+5 = 45; a3 = 5+2+15 = 22;
b1 = 10+5+5 = 20; b2 = 2+35+2 = 39; b3 = 8+5+15 = 28;
Pe = (a1*b1 + a2*b2 + a3*b3) / (87*87) = 0.455
K = (Po-Pe) / (1-Pe) = 0.4293578
这样我们就得到了kappa系数。
实际应用
像开头说的一样,真实的问卷回收回来后,我一般都会对用户的结果进行kappa系数计算之后才会发放奖励,因为我的奖励价格不低,也算是为了公司节省成本吧。
一般一个问卷我会让5个人去做,当然人越多越准确,但是为了考虑成本且就能得到有效的结果,我这里选了5个人,起初我的想法是用5个人的平均分做为标砖答案,然后让每个人的打分去和平均分算kappa,后来思考后发现这样有些不太合理,如果有一个人乱答,那么他的结果就会影响平均分,从而影响到整个结果。于是最终换成了一个人和所有人直接计算kappa,然后再求平均。这样当一个人乱作答的时候,我们在算出两两kappa的时候就可以发现这个人,然后在最终计算平均kappa的时候,去掉这个所有人和这个人之间的值即可。
刚开始我用python实现了kappa系数计算的代码,直接算出了一组结果,然后发现大家相互之前的kappa系数都非常的低,大概在0.1-0.2左右,后来分析是由于5分制导致数据太离散,因此针对翻译引擎的评测,我将用户打分的5分制换算成了3分制,1、2分归为一类,2为一类,4、5为一类。
当然在完成了这些之后,为了再多一轮保险,每一份问卷中的5个人中,有一个我非常信任的专业评测者,因此我还会计算所有人和她直接的kappa,这样更加的保证每一个打分的结果合理性和相关性都竟在掌握之中。
下面是我实现的python脚本。
(代码。。。。
。。。待添加
说明:输入文件**** 待加入)
下面是其中一次问卷,我计算的 “所有人之间kappa的平均分” 和 “所有人和优秀评测者之间的kappa” 不言而喻,很明显下图中标红的这位用户的打分就不合格,经过我人工筛查,果然这个用户的打分的确非常的不合理。
(待加入图)
有了kappa系数的计算规则后,对于一些类似这样的打分规则,我们就有了更多的把握以及更了解我们的评测结果是否准确可靠。