hdu2665 求区间第k大（小？）【主席树or可持久化线段树or函数式线段树】

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2665

题目大意：感觉题目表述得不明不白的，给一堆不知道我也不知道什么数据范围的数，然后给你M个区间，输出每个区间的第k大的数（这里出现严重的问题！！！）
题目说得kth bigger 难道不是第k大？结果我WA了一堆之后，翻了几篇别人的博客代码，结果发现别人好像都是求第k小 AC的。。。。然后换成求第k小，果然过了。。。。。。。。。。。。。。
大概是我英语不好。。。或者代码本来就打挫了。。。。

总之，大体的思路是用主席树，不过据说划分树时间更快内存更小，然而我并不会（咸鱼一会就去补）。。

刚敲的时候MLE了几次，因为多了一些无关紧要的变量。。
然后因为不知道给的是什么范围的数据，保险起见，做了离散化处理。。。。

OK ，进入正题。。这棵坑爹的主席树。。

主席树（或者叫可持久化线段树、函数式线段树），基本的思想其实就是对于【1，n】区间里所有的前缀区间（【1，1】，【1，2】。。。。。【1，n】），都给这些区间建立一个线段树，也就是说，需要n棵线段树。
注意，不是在上述的前缀里继续划分，而是以这些区间里的数为基础建立线段树。

好，为了方便表述，我们定义小写字母代表我原本长度为n的那堆数所对应的区间，比如【1，j】
用大写字母来表示我所建立的线段树上的结点所对应的区间，比如结点T上的区间是【L，R】
一个是原本的序列的，一个是树上的，可能有点绕，不急，后面还有更绕的。。。

线段树上区间【L，R】保存的应该是数的大小（经过离散化之后的，也就是第L大到第R大的数），也就是说，第j棵线段树应该存的是【1，j】区间里，数的大小在【L，R】这个范围内的个数有VAL个；
举个栗纸：
1 2 3 4 5 一共5个数
第一棵线段树 只保存 1 这个序列对应的线段树
第二棵 是 1 2 这个序列对应的线段树
以此类推是
1 2 3
1 2 3 4
1 2 3 4 5

而在第一棵树上，区间【1，5】 的值应该是1，因为在序列前缀里1到5的值只出现了1次
第二棵树上，区间【1，5】的值会是2，因为1、2这两个数都在【1，5】的范围内；
第三棵树也如此，往下推一下，第三棵树的区间【1，2】的值是2，区间【3】的值是1；
以此类推。。

好了，现在问题来了，这样子要建n棵线段树，内存炸得不要不要的；
假如road【j】代表序列的第j个数（离散化过的！！）
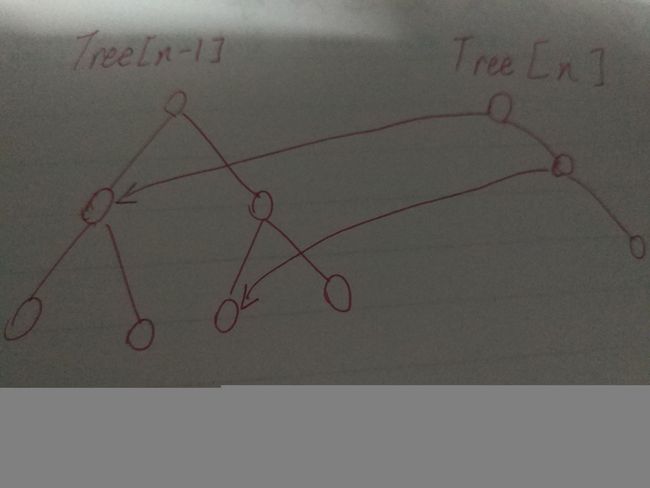
但细心观察下，可以发现，在【1，j】和【1，j+1】这两个前缀之间的差异仅仅是一个road【j+1】，也就是说，在【1，j】的树上，假如road【j+1】这个值是在【1，j】的左子树的那些区间上的，那么【1，j】和【1，j+1】对应树的右子树应该是一样的；

比如刚才举的那个栗纸，对于j=4的情况，【1，j】和【1，j+1】
当我需要建立第五棵线段树的时候，
这棵线段树上，【1，5】的值，比前一棵的多1，
在【1，3】这个区间的值上，与前一棵树对应区间的值完全一样，而【1，3】区间子树也是如此；

不难发现，其实每次往这些线段树里新增一个数值的时候，我们并不需要重新新建一棵完整的树，取而代之的是可以仅仅新建logn个结点，其它结点与上一个前缀区间共享

上图

好，到现在为止，我们就可以得到【1，j】这个区间里，【L，R】范围的数的数目了，然后只要求一个【1，i-1】的【L，R】范围的数的数目，两者相减就是【i，j】的【L，R】范围的数的数目了；
然后我们知道了这个范围的数目，就可以通过在左右子树里准确地找到第K小的数了（具体实现下面列举）。

主席树的实现：
因为每个结点只要新增logn个结点，所以n个结点的空间复杂度就是nlogn
为了方便操作，先建立一棵空的线段树，因为有n个数，离散化之后所有的数肯定都在【1，n】这个范围以内的，也就是说，每棵树对应位置的结点表示的区间都是相同的；（刚开始就是因为智障了多开了两个变量LR来表示区间，导致MLE。。。orz）
插入新结点的时候，可以用新结点和上一棵树对应位置的结点同时进行递归，就可以实现每个位置都共享左孩或者右孩了；
在进行查询的时候，对于区间【i，j】，应该同时对第i棵树和第j棵树进行递归，在寻找第k小的树时，先求出两棵树的当前区间【L，R】的左半部分区间（也就是左孩）对应数值的差，这样可以得出【i，j】里，【L，M】的范围的数的个数，然后判断一下k是否大于这个值，小于或者等于的话，说明第k大的数就在左孩区间里，这时候往左孩里走；大于的话，说明第k大不在这个区间里，而在【M+1，R】这个范围里，因为【L，M】的个数都不够k大，这时候应该要往右孩区间里找第k-num（【L，M】）小的数，因为左孩区间里已经有这么多个数比k小了，往右孩出发的时候就得先减去这些的个数。

大体上如此，如有错误请斧正

AC代码：

#include 

using namespace std;

int tot;
int n;
struct tr
{
    int val;
    int lc;
    int rc;
}tree[100001*20];

int node[100001];

int hah[100001];

int save[100001];

void build(int l,int r)
{
    int id=tot;
    if(l==r)
        return ;
    int m=(l+r)>>1;
    tree[id].lc=++tot;
    build(l,m);
    tree[id].rc=++tot;
    build(m+1,r);
}

void push(int x,int old,int las,int l,int r)
{
    int m=(l+r)>>1;
    tree[las].val=tree[old].val+1;
    if(l==r)
        return ;
    if(x<=m)
    {
        tree[las].rc=tree[old].rc;
        tree[las].lc=++tot;
        push(x,tree[old].lc,tot,l,m);
    }
    else
    {
        tree[las].lc=tree[old].lc;
        tree[las].rc=++tot;
        push(x,tree[old].rc,tot,m+1,r);
    }
}

int query(int s,int t,int k,int l,int r)
{
    if(l==r)
        return l;
    int cnt=tree[tree[t].lc].val-tree[tree[s].lc].val;
    int m=(l+r)>>1;
    if(k<=cnt)
    {
        return query(tree[s].lc,tree[t].lc,k,l,m);
    }
    else
    {
        return query(tree[s].rc,tree[t].rc,k-cnt,m+1,r);
    }
}


int shit()
{
    int s;
    int t;
    int k;
    scanf("%d %d %d",&s,&t,&k);
    //k=t-s+2-k;
    return query(node[s-1],node[t],k,1,n);
}


int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int m;
        scanf("%d %d",&n,&m);
        memset(tree,0,sizeof(tree));
        tot=1;
        build(1,n);
        int cnt=1;
        map<int,int> mp;
        for(int i=1 ; i<=n ; i++)
        {
            scanf("%d",&hah[i]);
            save[i]=hah[i];
        }
        sort(save+1,save+n+1);
        for(int i=1 ; i<=n ; i++)
        {
            if(mp[save[i]]==0)
                mp[save[i]]=cnt++;
        }
        for(int i=1 ; i<=n ; i++)
        {
            hah[i]=mp[hah[i]];
        }
        unique(save+1,save+n+1);
        node[0]=1;
        for(int i=1 ; i<=n ; i++)
        {
            node[i]=++tot;
            push(hah[i],node[i-1],node[i],1,n);
        }
        for(int i=0 ; i<m ; i++)
        {
            int t=shit();
            printf("%d\n",save[t]);
        }
    }
    return 0;
}