检验方法、混淆矩阵、模型评估

假设

H0 ：零假设，不能轻易被否定的命题作为原假设

H1 ：把无把握的、不能轻易肯定的命题作为备择假设

如果一个统计检验的结果拒绝零假设（结论不支持零假设），而实际上真实的情况属于零假设，那么称这个检验犯了第一类错误。

反之，如果检验结果支持零假设，而实际上真实的情况属于备择假设，那么称这个检验犯了第二类错误。

尽量使后果严重的错误成为第一类错误．

• 先定义 α 显著水平
• 定义原假设，即按照常理推断出的情况
• 计算 P 值，如果 P>α 则拒绝原假设接受 H1 假设

独立性检验

秩和检验

验证两个样本是否服从同一分布

将两个样本合并后排序，得到每个样本单位的秩次。当几个数据的大小相同秩次却不相同时，最终的秩次取其算术平均。

H0 ：两个总体服从相同的分布

H1 ：两个总体服从不同的分布

显著水平为 a

求出样本数较少的那个总体的秩和T

查“秩和检验表”，得出临界值 T1(a) ， T2(a) ，若 T1(a)<T<T2(a) 则接受 H0

chi squared test ( X2 test)

fo : observed观察值

fe : expected期望值

X2=∑fo−fefe

独立性检验：

class\item	good	normal	bad	total
child	N11	N12	N13	N1⋅
teens	N21	N22	N23	N2⋅
aldot	N31	N32	N33	N3⋅
total	N⋅1	N⋅2	N⋅3	N⋅⋅

fe=N⋅1×N1⋅N⋅⋅

Degree of freedom(df) = (total row number - 1)(total column number -1)

T test

bbs

F test

---

confusion matrix

Wiki

confusion matrix of classification

actual\class	cat	dog	rabbit
cat	5	3	0
dog	2	3	1
rabbit	0	2	11

table of confusion

correctness\Predict	Positive	Negative
True	TP	TN
False	FP	FN

Type I error : FP 误判为阳性样本

Type II error: FN 误判为阴性样本

Error=TN+FP4

• relevant 相关

  which is correctly classified
  

  Relevant=TP+FN

• retrieved 预测为正例的(即检索出的)

  selected items,
  

  Retrieved=TP+FP

• Accuracy

ACC=TP+TNTP+TN+FP+FN

for the cat class

correctness\Predict	Positive	Negative
True	5	3
False	2	17

code

sklearn

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_true, y_pred)

confusion matrix plot

import itertools
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import confusion_matrix
def plot_confusion_matrix(cm, classes,
                          normalize=False,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    """
    This function prints and plots the confusion matrix.
    Normalization can be applied by setting `normalize=True`.

    Usage
    ---
    cnf_matrix = confusion_matrix(y_test, y_pred)
    np.set_printoptions(precision=2)
    plt.figure()
    plot_confusion_matrix(cnf_matrix, classes=class_names, normalize=True,
                          title='Normalized confusion matrix')

    """
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=45)
    plt.yticks(tick_marks, classes)

    if normalize:
        cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
        print("Normalized confusion matrix")
    else:
        print('Confusion matrix, without normalization')

    print(cm)

    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

P-R & F1

Wikipedia entry for the Precision and recall
Wikipedia entry for the F1-score

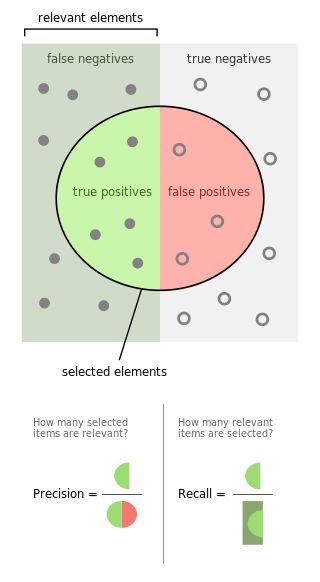
• precision查准率

  被 f 判定为正例的样本当中有多少实际为真？

  How many selected items are relevant?

• Precision=TPTP+FP={relevant}∩{retrieved}{retrieved}

• Recall查全率

  被正确分类的样本中有多少为真？

  How many relevant items are selected？

Recall=TPTP+FN={relevant}∩{retrieved}{relevant}

• F1 调和平均
  

  1F1=1p+1R2

• Fβ 加权调和平均
  

  1Fβ=1p+β2R1+β2

β>1 : Recall(查全)有更大影响, 宁可错杀无辜也不能放过坏人

β<1 : Precision(查准)有更大影响, 尽可能一查一个准减少冤假错案

理解查全率查准率的用处

在医学上HIV阳性就是Positive，但是有True Positive 和 False Positive之分。

实际得了HIV的患者有可能被检测为True Positive也可能被漏查了False Positive，统称为relevant相关。

如果是检验犯了第一类错误那么这个被检验为HIV阳性的的患者就是False Positive假阳性，也就是说他可以回家安心过他的好日子咯！

由于是HIV检测，因此查全率比较重要，不能放过每一个可能的患者啊。真阳TP和假阴FN都是实际得了HIV的患者，所以查全率——真阳占实际得病的比例，就变得非常的重要。

而查准率——真阳占判断为阳性的比例，在抓小偷的时候比较重要，不要造成冤假错案把好人当成小偷了！

code

sklearn

from sklearn.metrics import precision_recall_fscore_support
precision_recall_fscore_support(y_true, y_pred, beta=1.0, average='macro')

ROC(Receiver Operating Characteristic)

• True Positive Rate
  

  TPR=TPTP+FN=Presicion

• False Positive Rate

• FPR=FPTN+FP

  1. 将点集 (predict,y) 根据predict probability从小到大排列

  2. 设置截断点cut point从0一直到1， 求出TPR, FPR。

  假设当前阶段点为0.4，那么大于0.4的都预测为1

proba	0.05	0.14	0.32	0.46	0.57	0.68	0.73	0.89	0.93
predict	0	0	0	1	1	1	1	1	1
y	0	0	1	0	0	1	0	1	1
Count	TN+1	TN+1	FN+1	FP+1	FP+1	TP+1	FP+1	TP+1	TP+1

predict 为1的就是Positive，为0的就是Negative。

predict == y 的就是True，否则为False。

confusion matrix

Actual\Predict	0	1
0	2	3
1	1	3

table of confusion

Correctness\Predict	Positive	Negative
True	3	2
False	3	1

(FPR,TPR)=(25,34)

code

import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve

fpr,tpr,thresholds = roc_curve(y_true, y_score)
plt.plot(fpr,tpr, label='roc')
plt.legend()

AUC(Area Under ROC Curve)

即ROC曲线的面积。

AUC与排序误差 lrank 的关系：

AUC=1−lrank

from sklearn.metrics import roc_auc_score
AUC = roc_auc_score(y_true, y_scores)

---

sklearn classification metrics