20172304 实验二报告
- 课程:《软件结构与数据结构》
- 班级: 1723
- 姓名: 段志轩
- 学号:20172304
- 实验教师:王志强
- 助教:张师瑜&张之睿
- 实验日期:2018年11月5日-2018年11月12日
必修选修: 必修
实验要求
实验三-查找与排序-1
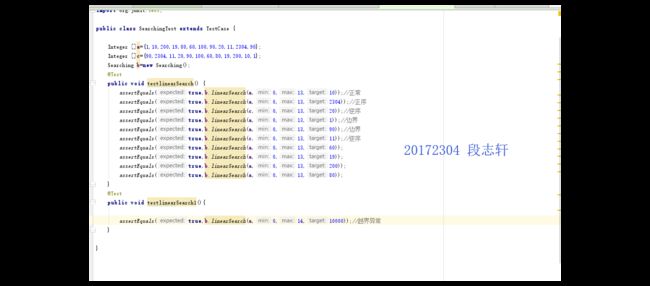
定义一个Searching和Sorting类,并在类中实现linearSearch(教材P162 ),SelectionSort方法(P169),最后完成测试。要求不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位提交运行结果图。
实验三-查找与排序-2
重构你的代码
把Sorting.java Searching.java放入 cn.edu.besti.cs1723.(姓名首字母+四位学号) 包中(例如:cn.edu.besti.cs1723.G2301)把测试代码放test包中重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种)
实验三-查找与排序-3
参考http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试提交运行结果截图
实验三-查找与排序-4
补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等(至少3个)
测试实现的算法(正常,异常,边界)
提交运行结果截图
实验三-查找与排序-5(选做,加分)
编写Android程序对各种查找与排序算法进行测试
提交运行结果截图
实验过程及实验结果
实验一过程及结果:
本次实验主要内容是对之前已经学习过的顺序查找和选择排序进行测试,实际上就是让我们再次熟悉一下junit测试的相关内容以及复习一下有关顺序查找和选择排序的相关内容。但是由于后续实验的内容都是在Sorting类以及Searching类的基础上继续改进的,所以在此我就不讲相关的码云链接给出,而只给出顺序查找以及选择排序的相关代码。
顺序查找
public static boolean linearSearch(T[] data, int min, int max, T target) {
int index = min;
boolean found = false;
while (!found && index <= max) {
found = data[index].equals(target);
index++;
}
return found;
} 选择排序
public static > T[] selectionSort(T[] data)
{
int min;
T temp;
for (int index = 0; index < data.length-1; index++)
{
min = index;
for (int scan = index+1; scan < data.length; scan++)
if (data[scan].compareTo(data[min])<0)
min = scan;
swap(data, min, index);
}
return data;
}
private static > void swap(T[] data, int index1, int index2)
{
T temp = data[index1];
data[index1] = data[index2];
data[index2] = temp;
} 
这是选择排序的图片

说明:由于要求至少十个测试用例,所以我将两个方法的测试的每种情况(正常,异常,边界,正序,逆序)在查找的测试中,虽然我不知道测试边界究竟有什么用,但是我还是查找了两个位于给定数组边界的两个元素,在设置异常的时候,考虑到实现的顺序查找的是需要给定的查找范围的,于是就给定了一个超过给定数组范围的范围,并且为他大度划分出了一个测试的空间,最后不出意外的出现了异常,抛出了ArrayIndexOutOfBoundsException,也就是我们认知意义上的数组越界异常。
在处理选择排序的时候,虽然还是不理解测试一个正序数组道德排序究竟有何意义,但是还是做了,并且为了满足10个用例的要求,最终也是每个情况做了多组数据的测试,但是考虑到排序算法似乎并没有所谓的什么边界,所以最终就没有做这方面的测试,在进行设置异常的时候。首先声明了一个Comparable数组,这个数组有个很神奇的地方就是它能够同时容纳不同类型的数据,所以我就在这个数组中储存了整数型的数据和文本型也就是String类型的数据。然后在进行排序的时候理所当然的就会出现异常。最终抛出的异常是ClassCastException: java.lang.Integer cannot be cast to java.lang.String,也就是类型转换异常:整数型变量不能转换为文本型变量。
实验二过程与结果
重构你的代码
把Sorting.java Searching.java放入 cn.edu.besti.cs1723.(姓名首字母+四位学号) 包中(例如:cn.edu.besti.cs1723.G2301)把测试代码放test包中重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种)
实验二的idea部分实际上并没有什么难度,只是换了一个位置,然后重新进行测试就是了。最后的结果和实验一雷同,于是就不在此放出图片了。然后就是命令行部分的实现了,出于严谨的态度,我请示了一下王老师,命令行模式是否也要在junit中进行测试,在得到肯定回答后就是噩梦的开始。首先上网上查资料。查到了首先应该是导入一个插件,也就是所谓的后缀为.jar的东西,下载之后就是导入的过程了。首先是找到导入位置,可能是太久没有人有勇气尝试在命令行中进行junit测试了,网上给定的教程的版本不知落后了我的虚拟机版本不知道多少辈子子孙孙。终于在费尽九牛二虎之力后,终于找到疑似目标之后,却又被权限困住了。还曾记得老师曾经教过我们,我们所学的是面向对象的设计是顶层设计,但是没想到自己最后却败在底层结构上了。图形界面没权限,命令行一般的移动命令mv似乎也不能识.jar这个东西。系统给我的提示是系统并不认为这是个文件,当时我就崩了,内心中犹如滔滔江水,泛滥而过,一发不可收拾。最终在挣扎与无奈中,伴随着12点钟声的响起,只能与我的实验二的另一半分数作别。别了,实验二的另一半。曾经有一份分数摆在我面前,我没有珍惜,如果上天能再给我一次机会,我会对他说:“junit还是idea的好。”
实验三过程与结果
决策树,这个的实现是基于书上的代码,这个实际上也没有也没有太大的难度
DecisionTree码云链接
CharacterAnalyzer
这是我设计的决策树
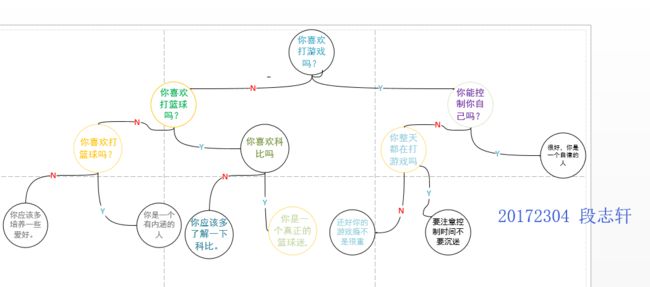
测试结果

实验三
这个实验主要就是要求我们阅读老师给定的博客,然后将相关算法补充完整,实际上,这更加类似于,将C++翻译成java的过程。除了实验一中已经使用过的顺序查找,这篇博客中还给出了二分查找,插值查找,斐波那契查找,平衡查找树,分块查找,哈希查找。处于治学严谨的态度,首先我要介绍着几种算法的原理。。
首先是顺序查找。
顺序查找顾名思义,就是按照顺序查找,就是从头开始依次向下进行。
然后二分查找是建立在已经排序好的数组的基础上的。首先由首尾两个数据算出将要作为标准的中间值,然后将查找目标与中间值进行比较。如果相等就返回true。如果小于中间值。则取中间值左面的数组,如果大于则反之。最后如果找到元素返回true,否则返回false。
下面是有关两个查找算法的动图
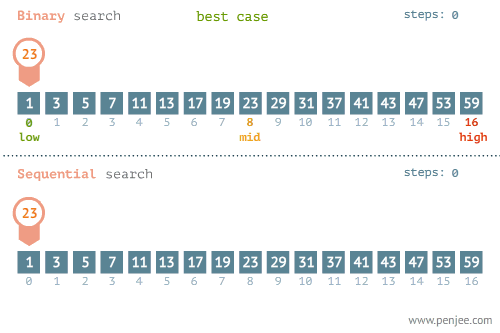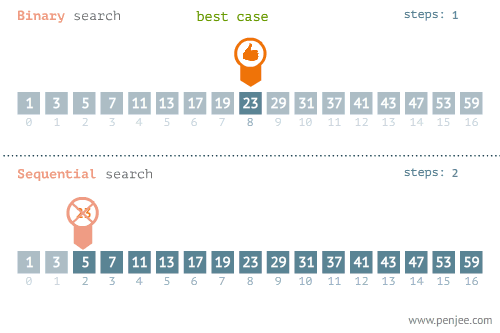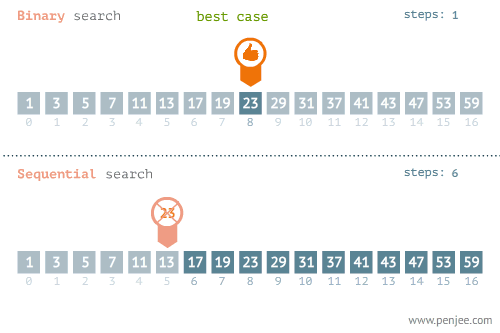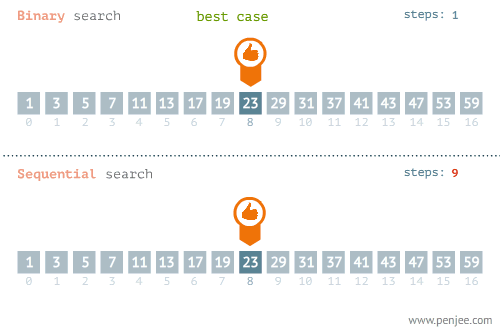
然后是插值查找,
其实插值查找时类似于二分查找的下面的公式中的第一行就是二分查找的公式,第二行是插值查找的公式。其中mid就是每次所确定的要与目标进行比较的值。而low和high就是每次重新划分完区域之后重新确定的最大值和最小值。可以看出插值查找通过改进算法,使得改进后的算法在面对分布较为均匀的数据时,有较好的效率。
mid=(low+high)/2, 即mid=low+1/2(high-low);
mid=low+(key-a[low])/(a[high]-a[low])(high-low),
插值查找示意图
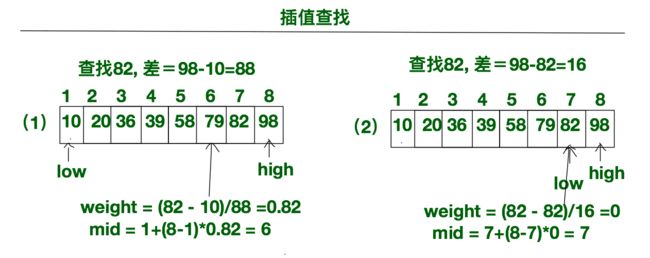
然后是斐波那契查找
相对于折半查找,一般将待比较的key值与第mid=(low+high)/2位置的元素比较,比较结果分三种情况:
1)相等,mid位置的元素即为所求
2)>,low=mid+1;
3)<,high=mid-1。 斐波那契查找与折半查找很相似,他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1,及n=F(k)-1;
开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种
1)相等,mid位置的元素即为所求
2)>,low=mid+1,k-=2;
说明:low=mid+1说明待查找的元素在[mid+1,high]范围内,k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个,所以可以递归的应用斐波那契查找。
3)<,high=mid-1,k-=1。
说明:low=mid+1说明待查找的元素在[low,mid-1]范围内,k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个,所以可以递归 的应用斐波那契查找。
斐波那契查找动态图

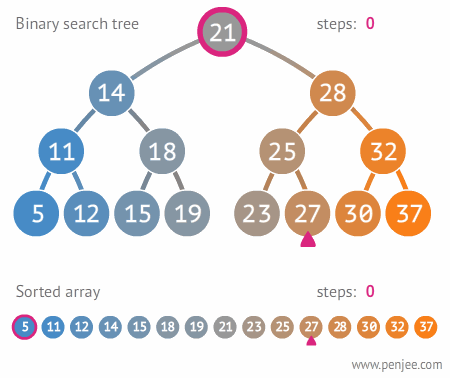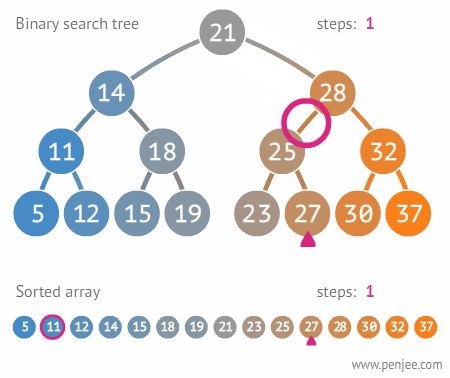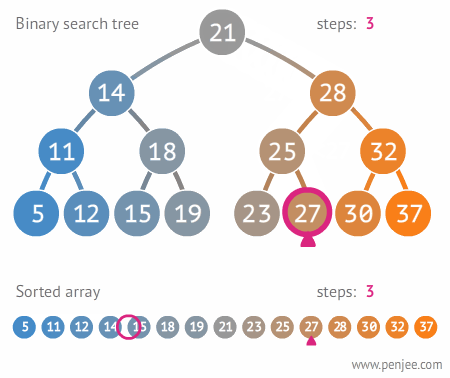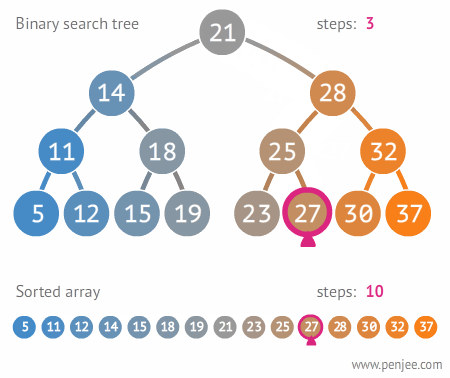
平衡查找树
这个实际上就是利用构建好的平衡查找树的性质来进行查找元素。平衡查找树构建要求右子树大于左子树。左子树小于右子树。且左右两子树高度差绝对值不超过一。
平衡查找树动态图展示。
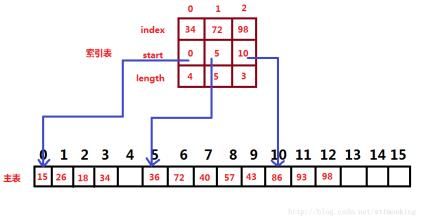
分块查找
要求将数据分成块,并且前一块的任一元素都不能大于后面块中的元素。所以这个算法应该是建立在数据已经排好序的的基础上道德。然后将每一块的最大元素取出然后建立一个索引列表。在将目标元素与索引列表中的元素进行比较,最后找到目标元素所在的分块,最后再次使用顺序或者二分查找进行查找,然后根据查找结果分别返回true或false。
分块查找图片展示
哈希查找
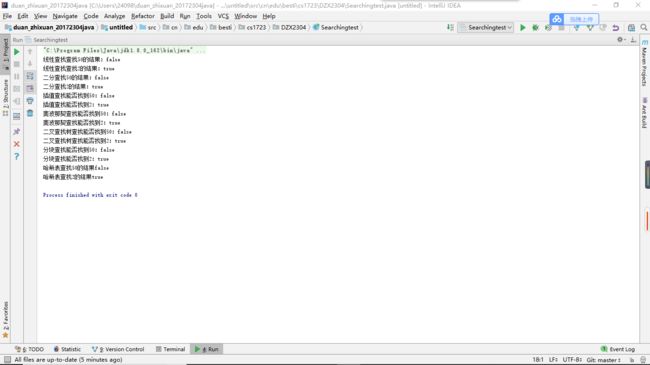
首先得将代查数据按照哈希规则存入哈希表中。所谓哈希规则就是将数据通过某种函数,来确定他在表中的位置。例如数据b=a%11,其中a表示数据,b表示数据在表中的位置,但是有时数据之间会产生冲突。例如。1%11=1,12%11=1,这时两个不同的数据却通过函数产生了相同的地址,这就是所谓的冲突。解决哈希冲突的办法有很多,但是其中最常用的就是链地址法。就是在数组中储存的并不是一个个具体的数据,而是链表,一旦发生冲突,就将数据插入到链表的末尾。在查找的时候也是遵循同样的规则的,首先将待查元素通过函数求得其目标位置,然后,在遍历链表,如果找到就返回true,如果没有找到就返回false。
实现代码。由于代码太多所以就将其置于下面链接之中。
Searching
测试类代码
package cn.edu.besti.cs1723.DZX2304;
public class Searchingtest {
public static void main(String[] args) {
Integer[] a={10,2,8,19,16,18,20,51,};//被查找的数组
Integer []a1={2,8,10,16,18,19,20,51};
Searching b=new Searching();
System.out.println("线性查找查找50的结果:" + Searching.linearSearch(a,0,7,50));
System.out.println("线性查找查找2的结果:"+Searching.linearSearch(a,0,7,2));
System.out.println("二分查找50的结果:" + b.BinarySearch1(a1,50,7));
System.out.println("二分查找2的结果:" + b.BinarySearch1(a1,2,7));
System.out.println("插值查找能否找到50:" + b.InterpolationSearch(a1, 50));
System.out.println("插值查找能否找到2:" + b.InterpolationSearch(a1,2));
System.out.println("斐波那契查找能否找到50:" + Searching.FibonacciSearch(a1,0,11, 50));
System.out.println("斐波那契查找能否找到2:" + Searching.FibonacciSearch(a1,0,11, 2));
System.out.println("二叉查找树查找能否找到50:" + b.BinarySearchTreeSearch(a,0,7,50));
System.out.println("二叉查找树查找能否找到2:" + b.BinarySearchTreeSearch(a,0,7,2));
System.out.println("分块查找能否找到50:" + Searching.partitionSearch(a,0,7,50));
System.out.println("分块查找能否找到2:" + Searching.partitionSearch(a,0,7,2));
System.out.println("哈希表查找50的结果" +b.Hashsearching(a,50));
System.out.println("哈希表查找2的结果"+b.Hashsearching(a,2));
}}实验四
这个实验主要是补充老师曾经讲过的排序算法,什么希尔排序堆排序以及二叉树排序,自己也可以实现排序算法。除了这两个排序算法之外,我还实现了插入排序和快速排序。
首先向大家介绍一下这几种算法。
首先是希尔排序,希尔排序的具体算法应用就是首先确定一个步长,从第一个元素开始,比较间隔步长-1个元素的元素,如果不符合与其的排序规则就交换两个元素。然后逐渐减少步长直至最后步长小于1为之。
希尔排序动态示意图
堆排序讲解
堆排序是一种比较复杂的排序,它是在二叉平衡树的基础上实现的。对分为两种,一种是大顶堆,大顶堆的所有子树的父结点都不小于其孩子结点。而小顶堆的所有子树的父结点都不大于他的孩子结点。我就简单介绍一下使用对进行排序的部分,而具体生成堆的部分我就不再赘言了。主要说一下使用堆进行排序的部分。以大顶堆为例。由于大顶堆的性质,导致最大的元素就是根节点,于是将根节点取出,然后将第一个非叶子结点取出,置为根节点。然后再次生成堆。依此类推。
堆排序动态展示
二叉树排序讲解
实际上二叉树排序实际上就是生成二叉查找树然后通过中序遍历就会得到排好序的数据。
二叉查找树生成动态示意图
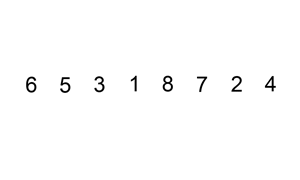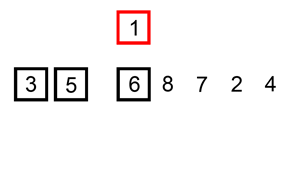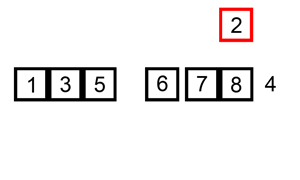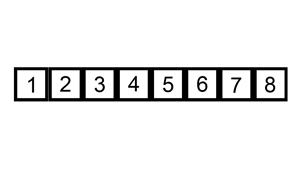
插入排序讲解
实际上插入排序就是从头开始遍历,将未排序的元素与已排序的元素逐个进行比较然后,直接将其插入到适合的位置。

插入排序示意图

快速排序
从数列中挑出一个元素,称为 “基准”(pivot);
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
快速排序动态展示
实现代码。由于代码太多所以就将其置于下面链接之中。
Sorting.java
测试类代码
package cn.edu.besti.cs1723.DZX2304;
public class SortingTest {
public static void main(String[] args) {
Comparable a[] = {10, 25, 2304, 44, 56, 11, 9, 8};
Sorting b = new Sorting();
Sorting.selectionSort(a);
System.out.println("选择排序后的数组");
for(Comparable c:a)
{
System.out.print(c+" ");
}
System.out.println();
Comparable a2[]= {10, 25, 2304, 44, 56, 11, 9, 8};
Sorting.insertionSort(a2);
System.out.println("插入排序后的数组");
for(Comparable c:a2)
{
System.out.print(c+" ");
}
System.out.println();
Comparable a3[]= {10, 25, 2304, 44, 56, 11, 9, 8};
Sorting.quickSort(a3);
System.out.println("快速排序后的数组");
for(Comparable c:a3)
{
System.out.print(c+" ");
}
System.out.println();
Comparable a4[]= {10, 25, 2304, 44, 56, 11, 9, 8};
Sorting.shellSort(a4);
System.out.println("希尔排序后的数组");
for(Comparable c:a4)
{
System.out.print(c+" ");
}
System.out.println();
Comparable a5[]= {10, 25, 2304, 44, 56, 11, 9, 8};
Sorting.heapSort(a5);
System.out.println("堆排序后的数组");
for(Comparable c:a5)
{
System.out.print(c+" ");
}
System.out.println();
Comparable a6[]= {10, 25, 2304, 44, 56, 11, 9, 8};
Sorting.binarySearchTreeSort(a6);
System.out.println("二叉查找树排序后的数组");
for(Comparable c:a6)
{
System.out.print(c+" ");
}
Comparable[] a7={10, "a", 2304, 44, "b", 11, 9, 8};
Sorting.binarySearchTreeSort(a7);
System.out.println("二叉查找树排序后的数组");
for(Comparable c:a7)
{
System.out.print(c+" ");
}
}
}测试结果截图

这里我放置了一组异常对照。
实验五
实验五是真的没什么好说的了,就是将代码在android上实现
代码调试时遇见的问题
问题:为什么斐波那契查找的结果和预期结果不一致
解决方案:后来发现是在进行斐波那契查找时没有使用已经排序好的数组。
其他
这次实验又是一次复习实验,经过多次的磨练相信我们对各种短发的理解会更加深入,对各种代码的运用会更加熟练。我们会不断地成长进步直至自己能开拓出一片属于自己的天空。参考资料
1.蓝墨云班课
2.java软件结构与数据结构