模电解析 第二章 大题

2-3答案：1A

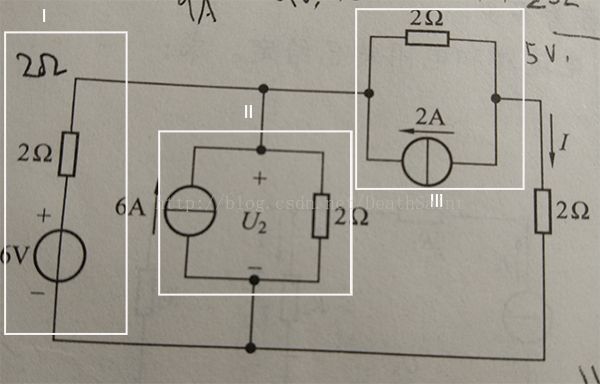
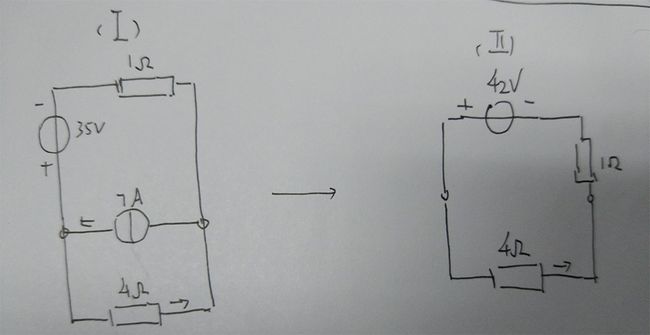
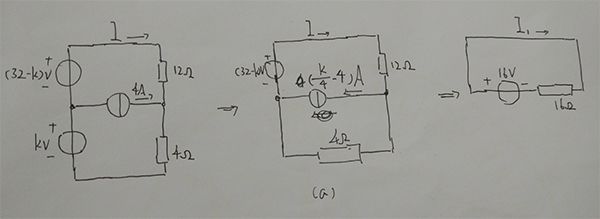
将I部分等效变换为理想电流源并联电阻，此时I部分和II部分共有两个理想电流源和两个电阻并联。将它们等效为一个理想电流源(Is)和一个电阻(Rs)并联（等效公式Is = I1 + I2，Rs = (R1*R2)/(R1+R2)）。将Is和Rs等效变换为理想电压源串联电阻。

将III部分等效变换为理想电压源串联电阻，此时的等效电路如下：

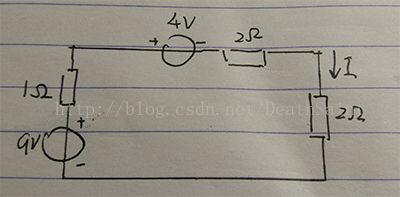
显然，I = 1A（注意两个理想电压源的参考方向是相反的）。

2-4答案：7.5V

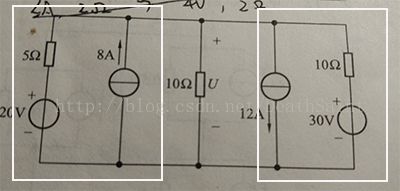
将上图被框起来的两个部分分别等效变换，变换过程为：一个理想电压源和一个理想电流源——>两个理想电流源——>一个理想电流源——>一个理想电压源。

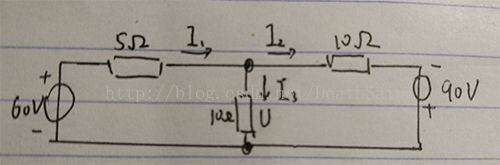
得到下图所示等效电路：

对左右两个回路分别KVL：

60V- 5Ω*I1 - U = 0; 90V - 10Ω*I2+ U = 0

对上节点KCL：

I1- I2 = I3

且U = I3*10Ω

联立解得 I1 = 10.5A，I2 = 9.75A，U = 7.5V。

 

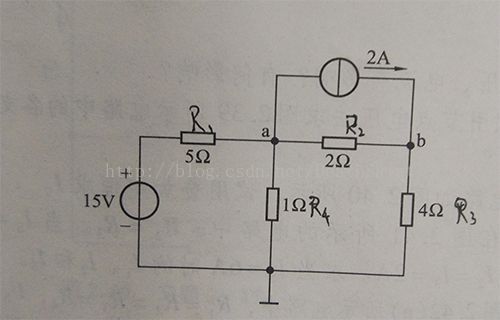
2-5答案：Ua ≈ 1.71V; Ub ≈ 3.80V

根据节点电压法列方程：

Ua(1/R1 + 1/R2 + 1/R4) - Ub(1/R2) = 15V/R1 - 2A

Ub(1/R2 + 1/R3) - Ua(1/R2) = 2A

解得Ua = (70/41)V ≈ 1.71V; Ub = (156/41)V ≈ 3.80V

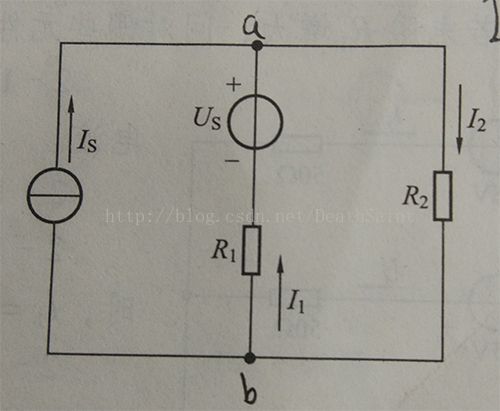
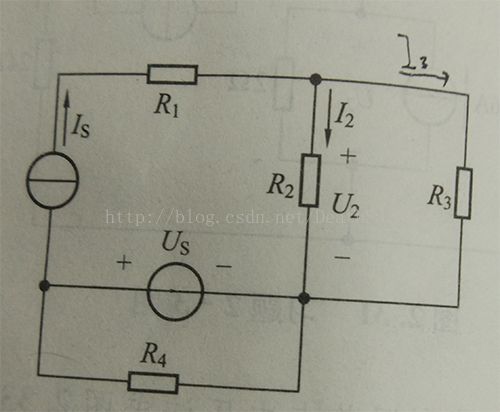
2-6答案：I1 = -1A; I2 = 4A

由KCl得：Is = I2 + I3，即I2 - I1 = 5A

对右回路KVL得：Us - R1*I1 - R2*I2 = 0

联立解得I1 = -1A; I2 = 4A

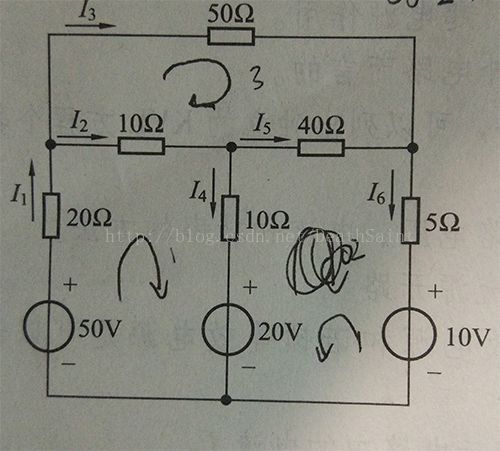
2-7答案：I1 ≈ 0.99A; I2 ≈ 0.65A; I3 ≈ 0.34A; I4 ≈ 0.38A; I5 ≈ 0.27A; I6 ≈ 0.61A

对各个节点KCL得：

I1 = I2 + I3; I2 = I4 + I5; I6 = I3 + I5; I1 = I4 + I6

列举所有独立KVL方程如下：

I3*50Ω - I2*10Ω - I5*40Ω = 0

50V - 20V - I1*20Ω - I2*10Ω - I4*10Ω = 0

10V - 20V + I6*5Ω + I5*40Ω - I4*10Ω = 0

将以上式子联立，解得：

I1 ≈ 0.99A; I2 ≈ 0.65A; I3 ≈ 0.34A; I4 ≈ 0.38A; I5 ≈ 0.27A; I6 ≈ 0.61A

2-8答案：I1 = -1A; I2 = 4A

(图见2-6)

根据网孔电流法列方程：

Im2*(R1+R2) - Im1*R1 = Us

Im1 = Is = 5A

Im2 = I2 = 4A

由KCL得：I1 = I2 - Is = -1A

2-9答案：I1 ≈ 0.99A; I2 ≈ 0.65A; I3 ≈ 0.34A; I4 ≈ 0.38A; I5 ≈ 0.27A; I6 ≈ 0.61A

(图见2-7)

根据网孔电流法列方程：

Im1*(20Ω + 10Ω + 10Ω) - Im3*10Ω + Im2*10Ω = 50V - 20V

Im2*(5Ω + 40Ω + 10Ω ) + Im3*40Ω +Im1*10Ω = 10V - 20V

Im3*(50Ω + 40Ω + 10Ω) + Im2*40Ω - Im1*10Ω = 0

且I1 = Im1; I2 = Im1 - Im3; I3 = Im3; I4 = Im1 + Im2; I5 = -(Im3 + Im2); I6 = -Im2

联立解得: I1 ≈ 0.99A; I2 ≈ 0.65A; I3 ≈ 0.34A; I4 ≈ 0.38A; I5 ≈ 0.27A; I6 ≈ 0.61A

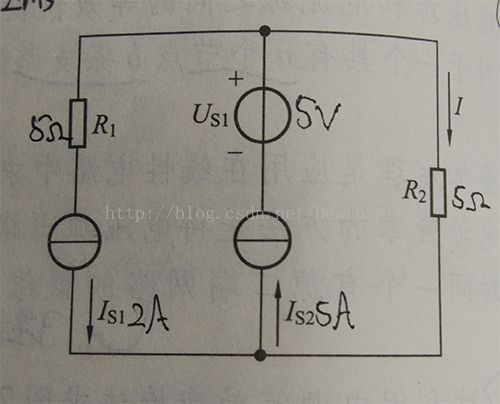
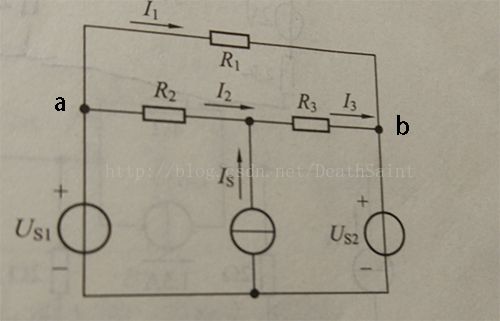
2-10答案：I = 3A; PIS1 = -10W; PIS2 = 50W; PUS1 = 25W

对左右回路分别KVL：

US1 - R2*I + UIS2 = 0

US1 + UIS1 + UIS2 = R1*IS1

由KCL得：I = IS2 - IS1 = 3A

代入解得：UIS1 = -5V; UIS2 = 10V

PIS1 = UIS1*IS1 = -10W; PIS2 = UIS2*IS2 = 50W; PUSI = US1*IS2 = 25W

验证功率守恒略。

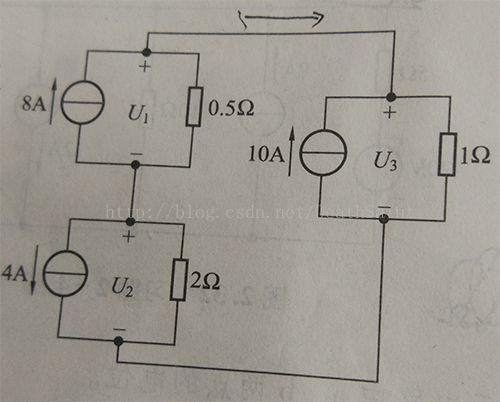
2-11答案：U1 = 6V; U2 = 0V; U3 = 6V

将U1,U2,U3分别视作单个元件，运用KVL得：U1 + U2 - U3 = 0

因为干路的电流的值处处相等，对每个节点KCL得：

8A - U1/0.5Ω = U3/1Ω - 10A = U2/2Ω - 4A

整理得：

2U1 + U3 = 18V

2U3 - U2 = 12V

4U1 + U2 = 24V

联立得：U1 = 6V; U2 = 0V; U3 = 6V

2-12答案：(1)U2 = Is*(R2*R3)/(R2+R3); I2 = Is*R3/(R2+R3); (2)理想电流源两端电压增大

注意到R2和R3并联，由并联电路的性质可知。R2两端电压U2等于R2和R3并联整体两端的电压，记为U总，且R总 =  (R2*R3)/(R3+R3)。故U2 = U总 = Is*(R2*R3)/(R2+R3); I2 = U2/R2 = IS*R3/(R2+R3)。

R1增大，由于R1与理想电流源串联，通过的电流不变，故过R1降低的电势增大。同理R2和R3两端的电压不变，通过的电流不变。根据KVl可知，理想电流源两端的电压需升高以满足沿回路绕行一周电势差为零。

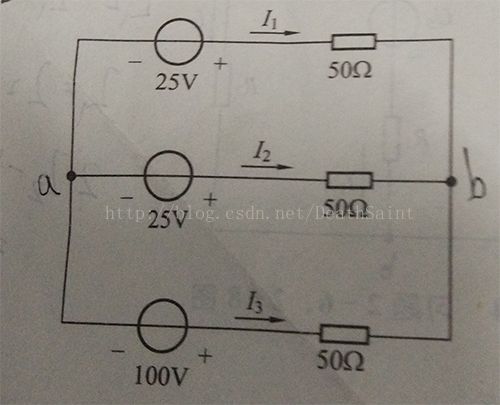
2-13答案：I1 = -0.5A; I2 = -0.5A; I3 = 1A

以b为参考节点，由于三个电阻的阻值相同，故设为为R，由节点电压法列方程：

Ua*3/R - Ub*3/R = - (R*I1 + R*I2 + R*I3)

由于b为参考节点，即Ub = 0，解得Ua = -50V。

且有Ua + 25V - R*I2 = Ub

所以I2 = -0.5A

对上下两个回路列独立KVL方程组，易得到I1 = I2 = -0.5A; I3 = 1A。

2-14答案：I = 1.4A

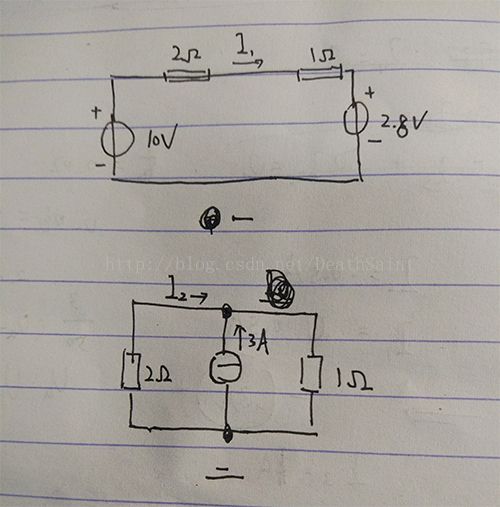
分别将电流源和电压源置零，得到下图所示两个电路。

电路一易得I1 = 2.4A。

电路二将理想电流源与并联的左电阻视为一个整体的电源，易得外电路电流为2A，由KCL得I2 + 3A = 2A，I2 = -1A

I = I1 + I2 = 1.4A

2-15答案：I1 = 3A; I2 = -1A; I3 = 5A

Is = 0时可等效为电流源被置零，现将电压源置零，考察Is = 6A的情况。

由KVL可知，此时R2和R3上降低的电势数值相等，且因为R2 = R3，故通过R2和R3的电流的值相等且方向相反。即I2' = -3A; I3' = 3A， 此时节点a和节点b的电压相等，故R1两端无电流通过，即I1' = 0A。

叠加得到：I1 = 0 + 3 = 3A; I2 = 2 - 3 = -1A; I3 = 2 + 3 = 5A

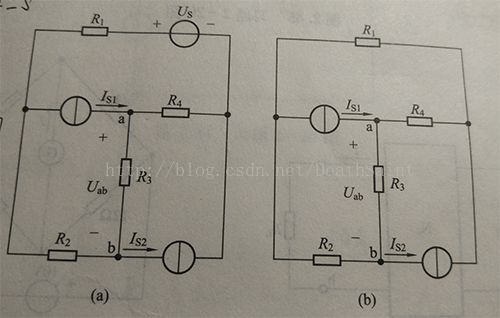
2-16答案：Uab = 16V

图(b)相当于将图(a)中电压源置零，由叠加定理可知，将图(a)中Uab的值减去图(a)电流源置零后U'ab的值，即为图(b)中Uab的值。

因为R1 = R2 = R3 = R4，故U'ab = -Us/4 = -4V，Uab = 12 - (-4) = 16V。

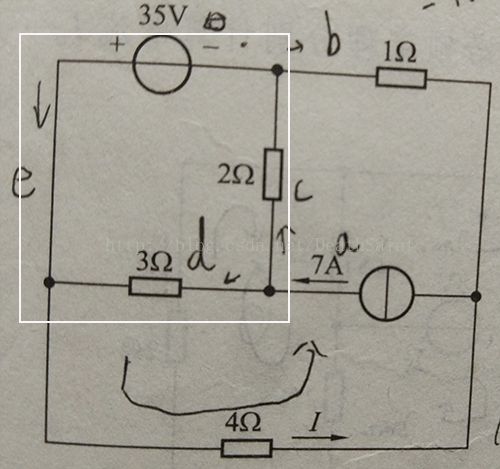
2-17答案：I = 8.4A

分别将电流源和电压源置零。

电流源置零时：I' = 35V/(4Ω + 1Ω) = 7A

电压源置零时，由KCL得：(d + e) + b = a，由KVL得3Ω电阻和2Ω电阻的电压降均为0。

故可将图中方框内的电路忽略，视为一个节点，得到的等效电路为理想电流源并联两个电阻。I'' = 7A*1Ω/(1Ω + 4Ω) = 1.4A

叠加得：I  = I' + I'' = 8.4A

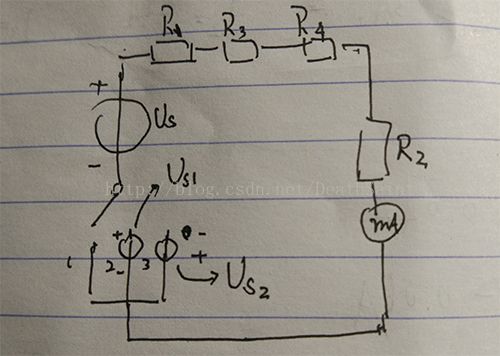
2-18答案：190mA

将电路等效变换为上图所示，令R = R1 + R2 + R3 + R4，并有：Us/R = 40mA; (Us + Us1)/R = -60mA。

由此可得：(Us - Us2)/R = 190mA

2-19答案：I = 8.4A

由2-17的分析可得等效电路I，由I得到戴维南等效电路II。I = 42V/(1Ω+4Ω) = 8.4A

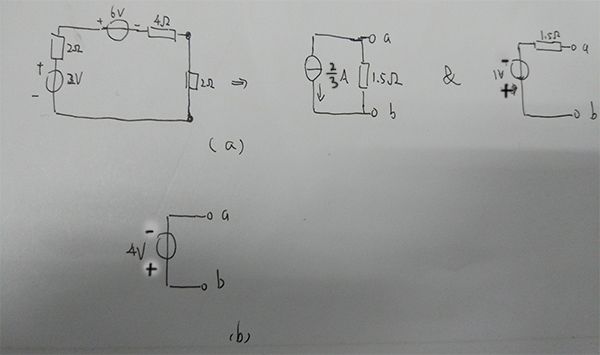
2-20答案：(a)R = 1.5Ω，U = -1V，I = -2/3A;  (b)R = 0Ω，U = -4V

考察（b）的原电路，因为理想电压源电阻为零，所以与其并联的电路部分相当于被短路，可忽略不计，由此忽略理想电流源和电阻，得到上图中的戴维南等效电路。

2-21答案：R = 18/11Ω，Us = 90/11V

Us/R = 5A，Us/(R+2Ω) = 2.25A，R = 90/11Ω，Us = 18/11V

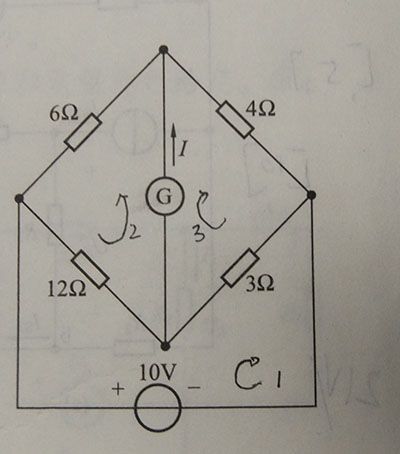
2-22答案：R = 5Ω时I = -0.204A；R = 10Ω时I = -0.135A；R = 20Ω时I = -0.08A

如图所示，分别设三个网孔为m1，m2，m3，I = Im2 + Im3，由网孔电流法得到如下方程组：

15Im1 + 12Im2 - 3Im3 = 10

(18+R)Im2 + 12Im1 + RIm2 = 0

(7+R)Im3 - 3Im1 + 5Im2 = 0

分别代入R = 5Ω，R = 10Ω，R = 20Ω求解即可。

2-23答案：(a)1A; (b)-0.67A

(a)的电路等效变换如上图所示。

对于(b)，则采用网孔电流法进行计算，如下图所示设Im1，Im2，Im3。

列方程：

6Im1 - 2Im3 = 8

3Im2 + 2Im3 = 8

6Im3 - 2Im2 + 2Im1 = 0

解得Im3 = I = -0.67A

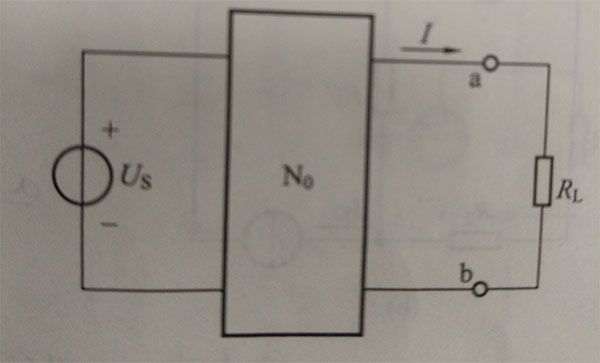
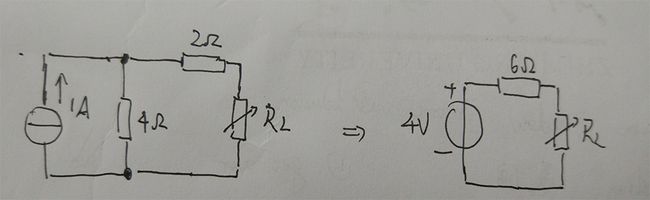
2-24答案：RL = 6Ω，P = 2/3W

进行如图所示变换，可认为RL连接在4V、内阻为6Ω的电源两端，故 RL与内阻相等时取得最大功率。

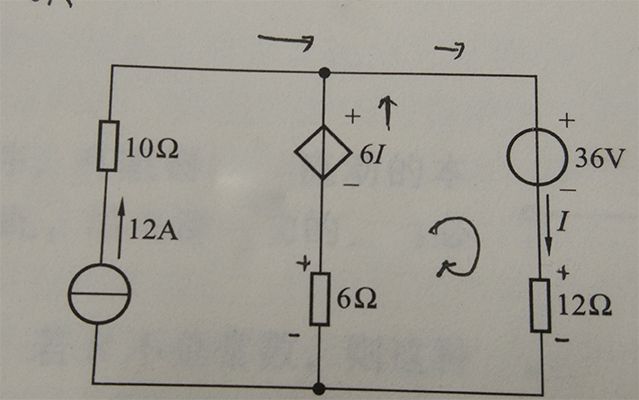
2-25答案：I = 3A

对右回路kvl，得-36V - 12Ω*I - 6Ω*I' + 6I = 0，整理得-6I' - 6I = 36V

由kcl得，I' + 12A = I

解得，I' = -9A，I = 3A 

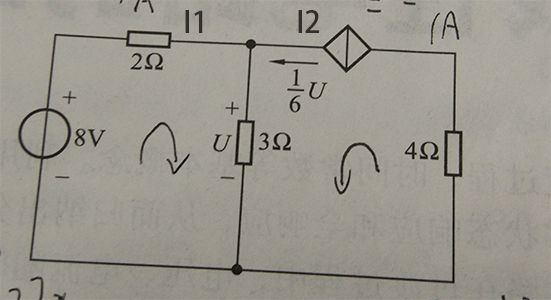
2-26答案：U = 6V

由kvl得：

8V - 2Ω*I1 = U = 3Ω*I

由kcl得，I = I1 + I2；I2 = (1/6)U

整理，解得：I1 = I2 = 1A，U = 3Ω*(I1 + I2) = 6V