树状数组
(我又来写题解了~~~)
树状数组(二叉搜索树)
定义: c[i] 维护的是 [i,i−lowbit(i)+1] 这段区间的值,这个 lowbit 等会解释。树状数组,他的时间复杂度为 O(logN) ,而且常数小,还好写,简直就是oi中的大法。并且我们可以“感受”到,如果只有一般的修改与一般的询问最大值,前缀和等,都完全可以替代线段树。(当然,有些时候他也替代不了线段树,比如主席树时)。下面来直观看看这个数组c的管辖范围。
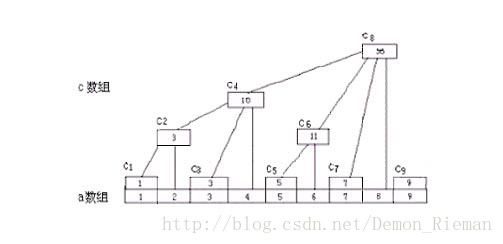
由此可见,这个数组像一棵树一样,故曰树状数组(实际上本来就是一棵树)。
下面解释 lowbit(x) 的含义: lowbit(x) 是最大的 2k ,使得 2k 是 x 的约数,而 2(k+1) 不是其约数。即 x 的约数中最大的二的幂。也可以说是 x 在二进制时最后一个 1 所代表的值。
1.基本操作:
单点更新:
int update(int x,int val)
{
while (x<=n)
{
c[x]+=val;
x+=lowbit(x);
}
}区间查询:
int query(int x)
{
int ans = 0;
while (x)
{
ans += c[x];
x-=lowbit(x);
}
}实际上也可以区间更新,区间查询。记录一个新数组 a[i]=x[i]−x[i−1] (原数组为 x ),那么修改时修改差分,然后差分的前缀和就是单点的数。而区间查询则需要推公式,推出来为 x×∑a[i]−∑a[i]×(i−1) ;那么就只需要再记录一个新的数组记录 a[i]×(i−1) 。
例题
- Codevs 1082
题目:区间修改,区间查询。
代码:
#include- Bzoj 1452: [JSOI2009]Count
题目: 略
题解:水题啊,注意到 c 的值很小, m , n 的也很小,那么我们就记录树状数组 c[d][m][n] 表示 d 这个数在 (0,0)—(m,n) 这个矩形内出现次数,然后就完了。
代码:
#include- bzoj 2743[HEOI2012]采花
题目:
萧芸斓是Z国的公主,平时的一大爱好是采花。
今天天气晴朗,阳光明媚,公主清晨便去了皇宫中新建的花园采花。花园足够大,容纳了n朵花,花有c种颜色(用整数1-c表示),且花是排成一排的,以便于公主采花。公主每次采花后会统计采到的花的颜色数,颜色数越多她会越高兴!同时,她有一癖好,她不允许最后自己采到的花中,某一颜色的花只有一朵。为此,公主每采一朵花,要么此前已采到此颜色的花,要么有相当正确的直觉告诉她,她必能再次采到此颜色的花。由于时间关系,公主只能走过花园连续的一段进行采花,便让女仆福涵洁安排行程。福涵洁综合各种因素拟定了m个行程,然后一一向你询问公主能采到多少朵花(她知道你是编程高手,定能快速给出答案!),最后会选择令公主最高兴的行程(为了拿到更多奖金!)。
题解:
实际上就是问你区间上有几个落单的数。那么我们可以打一下标记,先把询问按左端点排序,然后记录每个数的下一个与其值相等的数的位置 next ,然后先把每个值第二个加入树状数组,接着做时,就遇到一个 i ,去掉 next[i] ,加上 next[next[i]] 。(因为这样就可以使如果只有一个,一正一负刚好可以抵了,反之,也对,把第二个也加上是考虑了第零个)。
代码:
#include- bzoj 1878: [SDOI2009]HH的项链
题解:
与上题相似,但这题按右端点排序。我们记录一个 a[i] 表示 i 是不是当前区间内 x[i] 这个值最靠右的( x 是原序列),然后就统计一下就完了。
代码:
#include- bzoj 4240: 有趣的家庭菜园
题目:略
题解:
(这题好啊)*最小交换次数就是最后序列的关于原位置的逆序对*,然后我们可以证明最后数列是一个先增后减的样子。(好不容易遇到一个我会证的,当然要证一证)。如下:首先最大的可以随便放,然后我们考虑他左边的第一个数 Ai ,那么 Ai 右边有比他大的了,所以 Ai 左边都不能比 Ai 大,所以 Ai 是 [1,i] 最大的,同理可证 Ai−1 也是 [1,Ai−1] 最大的,于是在最大的以左为单增,同理可证右边为单减。好了,接着把草从大到小排一次序,那么我们新放的数一定在已经放的数的最左边或最右边,然后开始贪心,每次加入其位置,然后看是放左边还是右边。因为大的已经放了,较小的无论怎么放都不会影响之前的大的,所以可以贪心。
总结:这道题最大的转点在于:最小交换次数就是最后序列的关于原位置的逆序对这一结论,一定要记熟。
代码:(压了行的,别打我)
#include1); int tmp=query(a[i].id);
ans+=min(tmp,head-1-tmp);}printf("%lld",ans);return 0;}
- bzoj 2131 : 免费的馅饼
(数据小点还可以dp的,气)。这个我实在是看的别人的,这里推荐一个写得好的:
http://m.blog.csdn.net/FromATP/article/details/64133191
代码:
#includereturn w1int lowbit(int x){return (x&(-x));}
int query(int x)
{ int ans=0;
while (x)
{ans = max(c[x],ans);
x -= lowbit(x);}
return ans;
}
void update(int x,int val)
{ while (x<=n)
{c[x] = max(c[x],val);
x+=lowbit(x);
}}
int main()
{
scanf("%d%d",&w,&n);
for (int i = 1;i<=n;i++){
scanf("%d%d%d",&ob[i].t,&ob[i].loc,&ob[i].v);
ob[i].w1 = 2 * ob[i].t + ob[i].loc;
ob[i].w2 = 2 * ob[i].t - ob[i].loc;
y[++cnt] = ob[i].w2;
}
sort(y + 1 , y + 1 + n);
cnt = unique (y + 1 , y + 1 + n) - y - 1;
for (int i = 1;i<=n;i++) ob[i].w2 = lower_bound(y+1,y+1+cnt,ob[i].w2)-y;
sort(ob + 1,ob + 1 + n);
for (int i = 1;i<=n;i++)
{
f[i] = ob[i].v + query(ob[i].w2);
answ = max(answ,f[i]);
update(ob[i].w2 , f[i]);
}
//for (int i =1;i<=n;i++)
printf("%d",answ);
return 0;
}
结语
树状数组大法好,好写又好调!!!