| 存储类别 |
顺序存储结构 | 单链表 |
|---|---|---|
| 存储分配方式 | 用一段连续的存储单元依次存储线性表的数据元素 | 采用链式存储结构,用一组任意的存储单元存放线性表的元素 |
| 时间性能 | 查找O(1)、插入和删除O(n) | 查找O(n)、插入和删除O(1) |
| 空间性能 | 需要预分配存储空间,分大了浪费,小了容易发生上溢 | 不需要分配存储空间,只要有就可以分配,元素个数不受限制 |
通过上面的对比,可以得出一些经验性的结论:
- 若线性表需要频繁查找,很少进行插入和删除操作时,宜采用顺序存储结构。若需要频繁插入和删除时,宜采用单链表结构。
- 当线性表中的元素个数变化较大或者根本不知道有多大时,最好用单链表结构,这样可以不需要考虑存储空间的大小问题。而如果事先知道线性表的大致长度,用顺序存储结构效率会高很多。
线性表、包括顺序表和链表
顺序表里面元素的地址是连续的,
链表里面节点的地址不是连续的,是通过指针连起来的。
![]()
简介
一种逻辑结构,相同数据类型的n个数据元素的有限序列,除第一个元素外,每个元素有且仅有一个直接前驱,除最后一个元素外,每个元素有且仅有一个直接后继。
线性表的特点:
(1)元素个数有限 (2)逻辑上元素有先后次序
(3)数据类型相同 (4)仅讨论元素间的逻辑关系
注:线性表是逻辑结构,顺序表和链表是存储结构。
1.顺序存储
顺序表,使用数组实现,一组地址连续的存储单元,数组大小有两种方式指定,一是静态分配,二是动态扩展。
注:线性表从1开始,而数组从0开始。
优点:随机访问特性,查找O(1)时间,存储密度高;逻辑上相邻的元素,物理上也相邻;
缺点:插入删除需移动大量元素。
顺序表相关的操作跟数组有关,一般都是移动数组元素。
这里说一下插入和删除时的边界条件,首先线性表从1开始,数组从0开始,单纯的文件说明不够直接,来看图说话吧。
插入时:对于线性表来说最小能插入的位置是1,最大能插入的位置是8(=7+1),所以 1<= index <=(7+1);移动数组元素时要注意,for (int i = count; i >= index; i--) { items[i] = items[i-1];}
删除时:只能在蓝色方块之间寻找节点删除,即1 <= index <= 7。移动元素,for (i = index; i < count; i++) { items[i-1] = items[i];}
2.链式存储
链表的定义是递归的,它或者为空null,或者指向另一个节点node的引用,这个节点含有下一个节点或链表的引用。
与顺序存储相比,允许存储空间不连续,插入删除时不需要移动大量的元素,只需修改指针即可,但查找某个元素,只能从头遍历整个链表。
Java中使用嵌套类来定义节点的抽象数据类型:
private class Node{
// 链表节点的嵌套类
T item; // 节点内容
Node next; // 后继节点
}
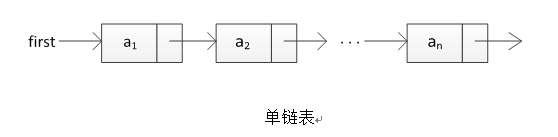
2.1 单链表
使用任意存储单元来存储线性表中的数据元素,节点类型如上。
单链表分为带头结点和不带头结点两种,不管有没有头结点,头指针都指向链表的第一个节点(有头结点指向头结点)。
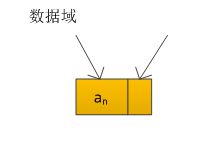
头结点:数值域可不设任何信息,头结点的指针域指向链表的第一个元素。
带头节点的好处有:
(1)链表第一位置节点上的操作和其它位置上的操作一致
(2)无论链表是否为空,头指针都指向头结点(非空),空表和非空表处理一样
(这里我没有使用头结点)
注:链表麻烦的地方是插入和删除时指针的修改,保证不断链,一般先断后链。
基本操作
1. 头插法
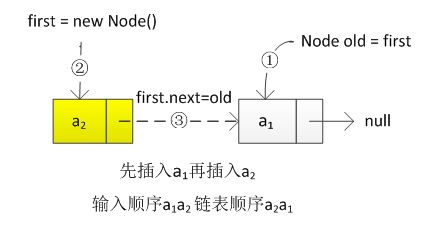
将新节点插入到当前链表的表头,(头结点之后),插入的顺序与链表中的顺序相反,关键点就是记住旧的表头,生成一个新的放到旧表头前面,如图:
核心代码:
public void headInsert(T item) {
Node old = first;
first = new Node();
first.item = item;
first.next = old;
count++;
}
2. 尾插法
增加一个尾指针,新节点插到链表的尾部,插入的顺序和链表的顺序一致,如图:
核心代码:
public void tailInsert(T item) {
Node old = last;
last = new Node();
last.item = item;
last.next = null;
if (isEmpty()) {
first = last;
} else {
old.next = last;
}
count++;
}
节点的插入和删除,要点是先断后连,关键就是不要断链了,以插入为例(把s插入p和q之间),先断意思是先把p->q断了,变成s->q,后连,最后再把p和s连接起来。
3. 插入节点
待插入节点为s,一般采用后插法,即先找到插入位置节点的前驱节点,然后插入,时间复杂度O(n)。
核心代码为: p=getNodeByIndex(i-1); s.next = p.next; p.next = s;
还有一种方法是,直接插入到位置的后面(前插法),然后交换两个节点的值,插入的节点到了指定位置,时间复杂度O(1):
核心代码: s.next = p.next; p.next = s; temp = p.item; // 交换内容 p.item = s.item; s.item = temp;
4. 删除节点
待删除节点为q,也是先找到前驱节点,修改指针域即可,时间复杂度O(n)。
核心代码: P = getNodeByIndex(i-1); q = p.next; p.next = q.next; q = null;
删除节点也能直接删除其后继节点,然后将后继节点的内容赋给自己即可,时间复杂度为O(1):
核心代码: q = p.next; p.item = p.next.item; p.next = q.next; q = null;
2.2 双链表
单链表节点的缺点是只有一个后继节点,访问前驱节点只能从头遍历(如插入、删除),时间复杂度为O(n)。双链表,即添加一个指向前驱的节点,节点类型如下:
private class Node{
// 链表节点的嵌套类
T item; // 节点内容
Node prior, next; // 前驱节点和后继节点
}
双链表的查找和单链表的相同再次不在赘述,双链表的构造也分为头插和尾插,与单链表唯一不同的是修改前驱指针prior,具体见源码。插入和删除时不同,因为需要修改两个指针,如果给定要操作的节点,插入和删除的时间复杂度为O(1)。
注:插入删除操作同样也是先断后连。
1. 插入节点
在p节点后插入s节点,先断后连,先把p和原后继节点的链条给断了,使后继节点只跟s节点有关:
①s.next = p.next; // 先断了p的后继 ②p.next.prior = s; // 在断了p后继的前驱 ③s.prior = p; // 让s的前驱指向p ④p.next = s; // p的后继指向s,重新连接上链条,此步必须在①②之后
2. 删除节点
删除节点p的后继节点q,也是先断后连,把q和其后继节点的关系,转让给p即可:
①p.next = q.next; // 先断了q的后继 ②q.next.prior = p; // 在断了q后继的前驱 删除节点q的前驱节点p,把p和去前驱节点的关系转让给q即可: ①q = p.prior.next; // 把p前驱节点的后继改成q ②q.prior = p.prior; // 把q的前驱节点改成p的前驱节点
2.3 循环链表
1. 循环单链表
与单链表的区别在于,表中最后一个节点的指针不为null,而改为指向头结点(第一个节点),从而整个链表形成一个环。判断循环单链表是否为空,判断是否等于头指针。
只有一个尾指针的循环单例表,可以很方便的操作表头和表尾,因为尾指针的后继就是头指针O(1) 。
2. 循环双链表
与双链表的区别在于,头结点的prior指针指向尾节点,尾节点的next指针指向头结点。
2.4 静态链表
静态链表是借助数组来描述线性表的链式存储结构,节点也有数据域和指针域,这里的指针是节点的相对地址(数组下标),也需要预先分配一块连续的内存空间。
特点,插入删除和动态链表一样,以next==-1为结束标志。
2.5 顺序表和链表的比较
1. 顺序表可以顺序存取,也支持随机存取;链表只能顺序存取。
2. 顺序表逻辑上相邻的物理上也相邻;而链表不一定,它是用指针来描述元素之间的关系。
3. 顺序表插入和删除要移动大量元素;链表只需修改指针即可