详解卡尔曼滤波原理
转载:https://blog.csdn.net/lybaihu/article/details/54943545
卡尔曼滤波原理及实现
前一段时间,做项目研究了一下卡尔曼滤波,并且在项目当中实现了一个物体跟踪的功能,所以,借着新鲜劲儿,本次博客对卡尔曼滤波进行一次整理。
- 卡尔曼滤波是什么
- 卡尔曼滤波能做什么
- 卡尔曼滤波的工作原理
- 举个栗子
卡尔曼滤波是什么
卡尔曼滤波适用于估计一个动态系统的最优状态。即便是观测到的系统状态参数含有噪声,观测值不准确,卡尔曼滤波也能够完成对状态真实值的最优估计。网上大多数的教程讲到卡尔曼的数学公式推导,会让人很头疼,难以把握其中的主线和思想。所以我参考了国外一位学者的文章,讲述卡尔曼滤波的工作原理,然后编写了一个基于OpenCV的小程序给大家做一下说明。下面的这个视频请大家先直观地看看热闹吧~
角度跟踪视频
卡尔曼滤波能做什么
假设我们手头有一辆DIY的移动小车。这辆车的外形是这样的: 
这辆车可以在荒野移动,为了便于对它进行控制,需要知道它的位置以及移动速度。所以,建立一个向量,用来存储小车的位置和速度
xk−→=(p→,v→)xk→=(p→,v→)
其实,一个系统的状态有很多,选择最关心的状态来建立这个状态向量是很重要的。例如,状态还有水库里面水位的高低、炼钢厂高炉内的温度、平板电脑上面指尖触碰屏幕的位置等等这些需要持续跟踪的物理量。好了,回归到正题,小车上面安装了GPS传感器,这个传感器的精度是10米。但是如果小车行驶的荒野上面有河流和悬崖的话,10米的范围就太大,很容易掉进去进而无法继续工作。所以,单纯靠GPS的定位是无法满足需求的。另外,如果有人说小车本身接收操控着发送的运动指令,根据车轮所转动过的圈数时能够知道它走了多远,但是方向未知,并且在路上小车打滑车轮空转的现象绝对是不可避免。所以,GPS以及车轮上面电机的码盘等传感器是间接地为我们提供了小车的信息,这些信息包含了很多的和不确定性。如果将所有这些信息综合起来,是否能够通过计算得到我们更想要的准确信息呢?答案是可以的! 
卡尔曼滤波的工作原理
1.先验状态估计
以之前我们创建的状态变量为例,
x→=[pv]x→=[pv]
下图表示的是一个状态空间图,为了研究方便,假如小车在一条绝对笔直的线路上面行驶,其位置和速度的方向是确定的,不确定的是大小。 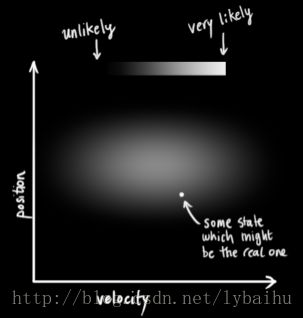
卡尔曼滤波器发生作用的前提是小车的速度和位置量在其定义域内具有正态的高斯分布规律。每一个变量都具有一个平均值μμ(这个值在变量的概率密度函数分布图的最中心位置,代表该数值是最可能发生的)和σ2σ2(这个数值代表方差,表示变量的不确定性程度)。下图中横纵坐标分别是位置和速度,相互独立,也就是已知其中一个变量,无法推断出另外一个的结果或者变化规律。 
下面请看另外一种情况:下图的位置和速度的分布不再像上图一样了,速度越大,位置也越大,这种情况下,两个变量相关(其实这种情况是很有可能发生的,因为速度越大的话,可能小车就远离我们,速度越小,表明靠近我们)。那么,通过协方差矩阵ΣΣ就能够将几个变量的相关程度描述清楚。矩阵当中的某一个元素ΣijΣij表示的是状态向量第i个变量和第j个变量之间相关程度,Σij=Cov(xi,xj)=E[(xi−μi)(xj−μj)]Σij=Cov(xi,xj)=E[(xi−μi)(xj−μj)] 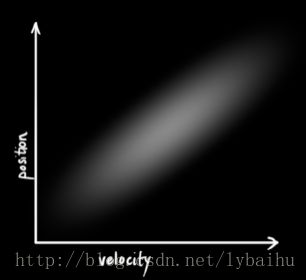
要注意的是协方差矩阵是一个对称阵。感兴趣的童鞋可以深入研究一下,协方差矩阵的特征值和特征向量所具有的几何意义:the directions in which the data varies the most.啥意思,就是哪个方向变化快,特征向量指哪儿。
协方差的特征向量是什么
协方差的几何意义
两个链接提供给大家,有兴趣的好好看看,知识点融会贯通了才有意思! 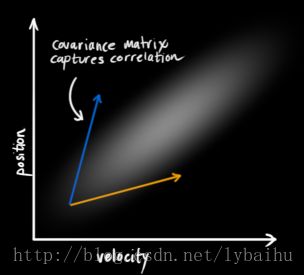
下面是重头戏:数学描述部分:
定义:
x^k=[positionvelocity]x^k=[positionvelocity]
Pk=[ΣppΣvpΣpvΣvv](1)(1)Pk=[ΣppΣpvΣvpΣvv]
x→kx→k是状态向量。PkPk称为协方差。
下图描述了一个k-1时刻x→k−1x→k−1和k时刻x→kx→k的状态:我们不清楚到底哪一个状态是最准确的,但是卡尔曼滤波的状态更新方程会根据前一时刻的结果预测出一个下一时刻的分布情况: 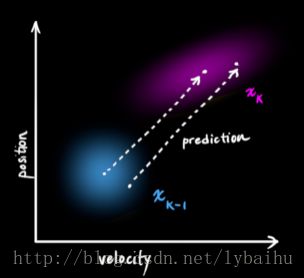
定义FkFk,这个矩阵表示的是前后两个状态之间是如何转换的:
pkpk=pk−1pk−1+δt+δtvk−1vk−1
vkvk= vk−1vk−1
写成矩阵的形式就是:
x^kx^k=[10δt1]=[1δt01]x^k−1x^k−1=FkFkx^k−1x^k−1(2)(2)
状态向量的更新有了,但是还缺少状态向量之间相关性的更新,也就是协方差矩阵。
Cov(x)=ΣCov(x)=Σ
Cov(Ax)=AΣATCov(Ax)=AΣAT
结合(2)得到:x^kx^k=Fk=Fkx^k−1x^k−1(先验状态估计向量)
PkPk=Fk=FkPk−1Pk−1FTkFkT(先验状态估计协方差矩阵) 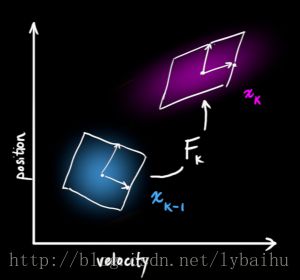
外部确定性影响
到目前为止,我们只是关心系统内部状态的更新,但是如果在外部对系统产生了确定影响,比如:小车的操控者发出一条刹车的指令,我们通过建模该指令,假如小车的加速度为aa,根据运动学的公式,得到:
p^kp^k==pk−1pk−1+δtδtvk−1vk−1+1212aaδt2δt2
vkvk=vk−1vk−1+aaδtδt 写成矩阵的形式就是:
x^kx^k=Fk=Fkxk−1xk−1+[δt22δt][δt22δt]aa=FkFkxk−1xk−1+BkBku→ku→k
其中,BkBk称为控制矩阵,uk−→uk→是控制向量,由于本例子当中的控制实际上只包含了加速度,所以该向量包含元素的个数为1。
外部不确定性影响
现实世界往往是不那么好描述清楚的,就是存在不确定的外部影响,会对系统产生不确定的干扰。我们是无法对这些干扰进行准确的跟踪和量化的。所以,除了外界的确定项,还需要考虑不确定干扰项wkwk。 
从而,得到最终先验估计的更新方程:
x^kx^k=FkFkxk−1xk−1+BkBku→ku→k+wkwk
每一次的状态更新,就是在原来的最优估计的基础上面,下一次的状态落在一个新的高斯分布区域,从坐标系上面看就像是一团云状的集合,最优的估计就在这个云团当中的某一处。所以,我们首先要弄清楚这个云团具有什么样的性质,也就是使用过程激励噪声协方差QkQk来描述不确定干扰。 
考虑到不确定的干扰之后,和不考虑这一因素相比,状态的期望不变,只是协方差产生变化,即wkwk的期望为0。 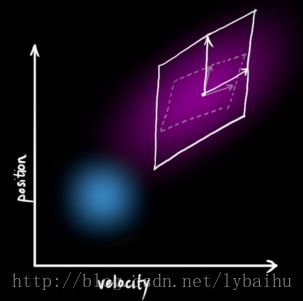
到此,先验估计的过程结束,总结一下,形成如下的公式:
x^kx^k=Fk=Fkx^k−1x^k−1+BkBku→ku→k+wkwk
P^kP^k=Fk=FkP^k−1P^k−1FTkFkT+QkQk(3)(3)
重点来了:
先验估计x^kx^k取决于如下三部分:一部分是上一次的最优估计值,一部分是确定性的外界影响值,另一部分是环境当中不确定的干扰。先验估计协方差矩阵PkPk,首先是依据第k-1次卡尔曼估计(后验估计)的协方差矩阵进行递推,再与外界在这次更新中可能对系统造成的不确定的影响求和得到。
2.后验估计(量测更新)
到此,利用xk^xk^和PkPk能够对系统进行粗略的跟踪,但是还不完善。因为安装在系统上面的传感器会对系统的状态进行测量反馈,纠正估计。下面看看传感器的量测更新是怎么样对最终的估计产生影响的。下图说明的是状态空间向观测空间的映射。
在这里需要说明一下,卡尔曼滤波器的观测系统的维数小于等于动态系统的维数,即观测量可以少于动态系统中状态向量所包含的元素个数。 
注意,传感器的输出值不一定就是我们创建的状态向量当中的元素,有时候需要进行一下简单的换算。即使是,有可能单位也不对应,所以,需要一个转换。这个转换就是矩阵HkHk,在一些文献当中也被称作状态空间到观测空间的映射矩阵。 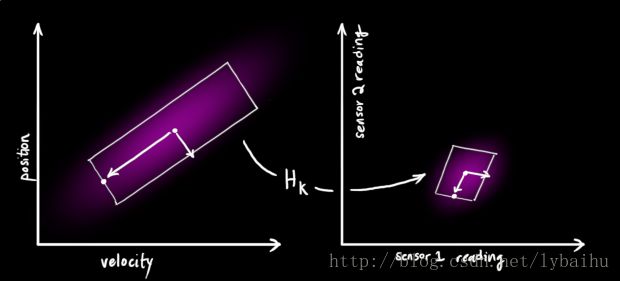
得到的公式如下:
μ→expected=Hkμ→expected=Hkx^kx^k
Σexpected=HkΣexpected=HkPkPkHTkHkT
那么,传感器对系统某些状态的测量真的准确吗?是不是也会有偏差呢?答案是肯定的。系统在某一个状态下,传感器输出一组观测值,当系统在另一个状态下,传感器会输出另外的观测值。反过来想,就是说根据读取到的观测向量,可以推测系统的实际状态。由于的存在,不同的系统状态造成当前的观测值的概率是不同的。所以,还需要一个观测噪声向量以及观测噪声协方差来衡量测量水平,我们将它们分别命名为v→kv→k和RkRk。下面的两张图说明这一点。 

z→tz→t=HkHkx^kx^k+v→kv→k
观测向量zk→zk→服从高斯分布,并且其平均值认为就是本次的量测值(z1,z2)(z1,z2)。
下图看到的是两个云团,一个是状态预测值,另一个是观测值。那么到底哪一个具体的结果才是最好的呢?现在需要做的是对这两个结果进行合理的取舍,通过一种方法完成最终的卡尔曼预测。即:从图中粉红色云团和绿色云团当中找到一个最合适的点。 
问题来了,怎么找?
首先来直观理解一下:考察观测向量zk→zk→和先验估计x^kx^k:存在两个事件:事件1传感器的输出是对系统状态真实值的完美测量,丝毫不差;事件2先验状态估计的结果就是系统状态真实值的完美预测,也是丝毫不差。但是大家读到这里心里非常清楚的一点是:两个事件的发生都是概率性的,不能完全相信其中的任何一个!!!!!!!
如果我们具有两个事件,如果都发生的话,从直觉或者是理性思维上讲,是不是认定两个事件发生就找到了那个最理想的估计值?好了,抽象一下,得到:两个事件同时发生的可能性越大,我们越相信它!要想考察它们同时发生的可能性,就是将两个事件单独发生的概率相乘。 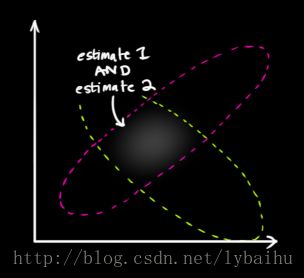
那么,下一步就是对两个云团进行重叠,找到重叠最亮的点(实际上我们能够把云团看做一帧图像,这帧图像上面的每一个像素具有一个灰度值,灰度值大小代表的是该事件发生在这个点的概率密度),最亮的点,从直觉上面讲,就是以上两种预测准确的最大化可能性。也就是得到了最终的结果。非常神奇的事情是,对两个高斯分布进行乘法运算,得到新的概率分布规律仍然符合高斯分布,然后就取下图当中蓝色曲线峰值对应的横坐标不就是结果了嘛。证明如下:
我们考察单随机变量的高斯分布,期望为μμ,方差为σ2σ2,概率密度函数为:
N(x,μ,σ)=1σ2π−−√e−(x−μ)22σ2(4)(4)N(x,μ,σ)=1σ2πe−(x−μ)22σ2
如果存在两个这样的高斯分布,只不过期望和方差不同,当两个分布相乘,得到什么结果? 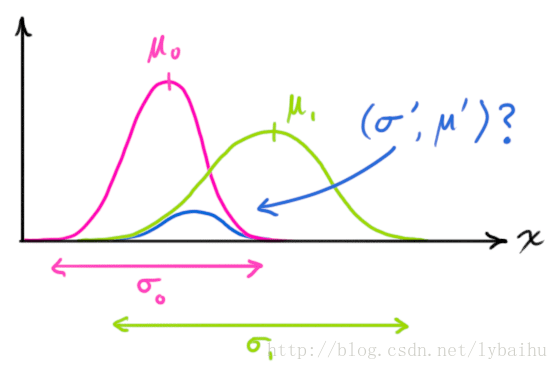
是不是下式成立
N(x,μ0,σ0)⋅N(x,μ1,σ1)=?N(x,μ′,σ′)(5)(5)N(x,μ0,σ0)⋅N(x,μ1,σ1)=?N(x,μ′,σ′)
将(4)带入(5),对照(4)的形式,求得
μ′μ′ = μ0μ0+k(k(μ1μ1- μ0μ0))
σ′2σ′2=σ20σ02- σ′2σ′2
其中,k=σ20σ20+σ21k=σ02σ02+σ12
以上是单变量概率密度函数的计算结果,如果是多变量的,那么,就变成了协方差矩阵的形式:
K=Σ0(Σ0+Σ1)−1(6)(6)K=Σ0(Σ0+Σ1)−1
μ→′=μ→0+K(μ→1−μ→0)(7)(7)μ→′=μ→0+K(μ→1−μ→0)
Σ′=Σ0−KΣ0(8)(8)Σ′=Σ0−KΣ0
K称为卡尔曼增益,在下一步将会起到非常重要的作用。
好了,马上就要接近真相!
卡尔曼估计
下面就是对传感器的量测结果和根据k-1时刻预测得到的结果进行融合。(由于刚才的推导是两个单变量,并且处在同一个空间内,下面的推导为了方便起见,我们将先验状态估计对应的结果映射到观测向量空间进行统一的运算)
第一个要解决的问题是:(7)和(8)两个式子中那个平均值和方差都对应多少?
(μ0,Σ0)=(Hkx^k,HkPkHTk)(9)(9)(μ0,Σ0)=(Hkx^k,HkPkHkT)
(μ1,Σ1)=(zk,Rk)(10)(10)(μ1,Σ1)=(zk,Rk)
将(9)和(10)代入(6)、(7)、(8)三个式子,整理得到:
Hkx^′k=Hkx^k+K(zk→−Hkx^k)(11)(11)Hkx^k′=Hkx^k+K(zk→−Hkx^k)
HkP′kHTk=HkPkHTk−KHkPkHTk(12)(12)HkPk′HkT=HkPkHkT−KHkPkHkT
其中,卡尔曼增益的表达式为:K=HkPkHTk(HkPkHTk+Rk)−1K=HkPkHkT(HkPkHkT+Rk)−1
最后一步,更新结果:
x^′kx^k′=x^kx^k+K′K′(zk→(zk→-Hkx^k)Hkx^k)(13)(13)
P′kPk′=PkPk-K′K′HkPkHkPk(14)(14)
K′K′=PkHTk(HkPkHTk+Rk)−1PkHkT(HkPkHkT+Rk)−1(15)(15)
x^′kx^k′就是第k次卡尔曼预测结果,P′kPk′是该结果的协方差矩阵,它们都作为下一次预测的初始值参与到新的预测当中。总体上来讲,卡尔曼滤波的步骤大致分为两步,第一步是时间更新,也叫作先验估计,第二步是量测更新,也叫作后验估计,而当前的卡尔曼过程的后验估计结果不仅可以作为本次的最终结果,还能够作为下一次的先验估计的初始值。下图是卡尔曼滤波的工作流程: 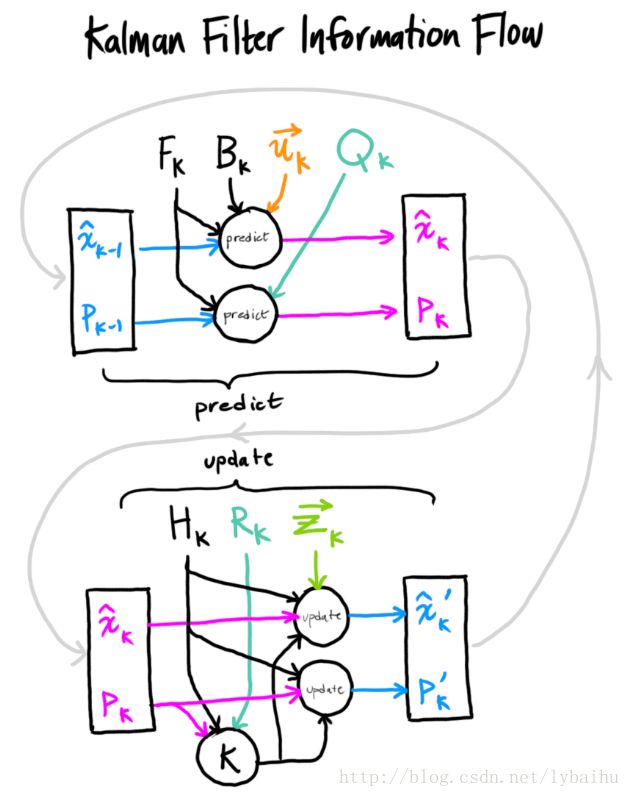
对卡尔曼滤波原理的理解,我参考了这篇文章,图片取自该文章,该文的图片和公式颜色区分是一大亮点,在此表示对作者的感谢。
举个栗子
这部分重点讲解一下利用OpenCV如何实现一个对三维空间内物体的二维平面跟踪。
背景:跟踪一个移动速度大小和方向大致保持不变的物体,检测该物体的传感器是通过对物体拍摄连续帧图像,经过逐个像素的分析计算,得到x、y方向的速度,将两个速度构成一个二维的列向量作为观测向量。
下面看一下OpenCV当中对卡尔曼滤波的支持和提供的接口说明。
OpenCV2.4.13-KalmanFilter
下面是参与到卡尔曼滤波的一些数据结构,它们代表的意义在其后面用英文进行了描述。
OpenCV将以下的成员封装在了KalmanFilter当中,我们使用时候,可以直接实例化一个对象,例如:
KalmanFilter m_KF;- 1
//CV_PROP_RW Mat statePre; //!< predicted state (x'(k)): x(k)=A*x(k-1)+B*u(k)
//CV_PROP_RW Mat statePost; //!< corrected state (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
//CV_PROP_RW Mat transitionMatrix; //!< state transition matrix (A)
//CV_PROP_RW Mat controlMatrix; //!< control matrix (B) (not used if there is no control)
//CV_PROP_RW Mat measurementMatrix; //!< measurement matrix (H)
//CV_PROP_RW Mat processNoiseCov; //!< process noise covariance matrix (Q)
//CV_PROP_RW Mat measurementNoiseCov;//!< measurement noise covariance matrix (R)
//CV_PROP_RW Mat errorCovPre; //!< priori error estimate covariance matrix (P'(k)): P'(k)=A*P(k-1)*At + Q)*/
//CV_PROP_RW Mat gain; //!< Kalman gain matrix (K(k)): K(k)=P'(k)*Ht*inv(H*P'(k)*Ht+R)
//CV_PROP_RW Mat errorCovPost; //!< posteriori error estimate covariance matrix (P(k)): P(k)=(I-K(k)*H)*P'(k)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
KalmanFilter类的成员函数具有如下几个:
KalmanFilter
init
predict
correct- 1
- 2
- 3
- 4
方法很简单,但是需要知道如何使用:
程序当中,我单独写了一个类,在我的计算线程(就是获取到量测结果的线程)当中对该类进行实例化并且调用其中的方法。量测结果存放在
m_dispacementVector[0] = m_xSpeed;
m_dispacementVector[1] = m_ySpeed;
当中。
步骤一:
CV_WRAP KalmanFilter( int dynamParams, int measureParams, int controlParams = 0, int type = CV_32F );
/** @brief Re-initializes Kalman filter. The previous content is destroyed.
@param dynamParams Dimensionality of the state.
@param measureParams Dimensionality of the measurement.
@param controlParams Dimensionality of the control vector.
@param type Type of the created matrices that should be CV_32F or CV_64F.
*/- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
在卡尔曼滤波类的构造函数成员列表当中首先告知OpenCV过程状态向量的维度和观测向量的维度:
m_KF(4,2,0)- 1
对m_KF成员的初始化:
1状态向量初始化xkxk
我想对物体的位置信息和速度信息进行跟踪,由于是二维的,所以位置信息x、y方向两个变量,速度信息x、y方向两个变量,从而m_KF.statePre和m_KF.statePost是一个四维列向量。
state=⎡⎣⎢⎢⎢⎢xyvxvy⎤⎦⎥⎥⎥⎥state=[xyvxvy]
该向量在初始化时设置为零。
2状态转移矩阵初始化FkFk
在计算机屏幕上面,我自定义了一个该物体的运动空间,具有横纵坐标,后面会看到这个空间。由于相机的帧率是30fps,所以相邻帧时间间隔δt≈30msδt≈30ms,被测物体的实际速度大约为10mm/s,所以在如此短的时间内,该物体能够认为是做匀速直线运动,故得到状态转移方程
Fk=⎡⎣⎢⎢⎢10000100δt0100δt01⎤⎦⎥⎥⎥Fk=[10δt0010δt00100001]
m_KF.transitionMatrix = (Mat_(4, 4) << 1, 0, 0.03, 0,0,1,0,0.03,0,0,1,0,0,0,0,1); - 1
3过程噪声激励协方差矩阵QkQk
setIdentity(m_KF.processNoiseCov, Scalar::all(1e-5));//Q- 1
认为过程激励噪声比较弱,并且每个分量相互之间不存在相关系。
4观测矩阵HkHk
setIdentity(m_KF.measurementMatrix);- 1
初始化得到:
Hk=[00001001]Hk=[00100001]
由于传感器只是检测到了两个方向的速度,对位移没有检测,所以要将矩阵前两列初始化为0。
5预测估计协方差矩阵PkPk
setIdentity(m_KF.errorCovPost, Scalar::all(1));- 1
初始化为单位阵。
6测量噪声协方差矩阵RkRk
setIdentity(m_KF.measurementNoiseCov, Scalar::all(1e-1));//R- 1
步骤二:
先验估计:
m_prediction = m_KF.predict();- 1
步骤三:
后验估计:
首先需要告知卡尔曼滤波器最新的传感器数据:
m_dispacementVector[0] = m_xSpeed;
m_dispacementVector[1] = m_ySpeed;- 1
- 2
m_pKalman->updateMeasurements(m_dispacementVector);
- 1
- 2
void kalmanFilter::updateMeasurements(double p[])
{
m_measurement = (Mat_<float>(2, 1) << p[0], p[1]);
}- 1
- 2
- 3
- 4
接着完成后验估计:
m_KF.correct(m_measurement);- 1
KalmanFilter.h:
#include - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
KalmanFilter.cpp:
#include "kalmanFilter.h"
#include float >(0, 0) << " " << m_measurement.at<float>(1, 0)<<" ";
myfile << "kalman" << " " << m_KF.statePost.at<float>(2, 0) << " " << m_KF.statePost.at<float>(3, 0) << endl;
}
double * kalmanFilter::returnResult()
{
double result[4];
for (int i = 0; i < 4; i++)
{
result[i] = m_postCorrectionState.at<double>(i, 1);
}
return result;
}
void kalmanFilter::drawArrow(Point start, Point end, Scalar color,int alpha,int len)
{
const double PI = 3.1415926;
Point arrow;
double angle = atan2((double)(start.y - end.y), (double)(start.x - end.x));
line(m_img, start, end, color,2);
arrow.x = end.x + len * cos(angle + PI * alpha / 180);
arrow.y = end.y + len * sin(angle + PI * alpha / 180);
line(m_img, end, arrow, color,1);
arrow.x = end.x + len * cos(angle - PI * alpha / 180);
arrow.y = end.y + len * sin(angle - PI * alpha / 180);
line(m_img, end, arrow, color,1);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
下面是录制的程序运行效果图(抱歉物体未显示): 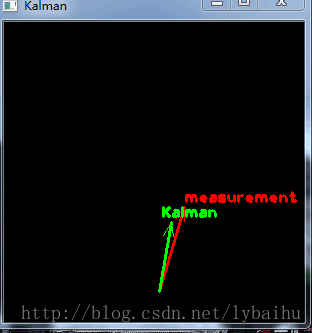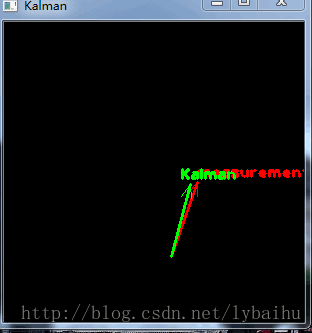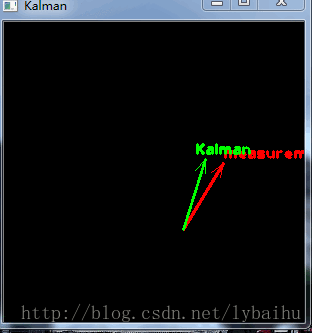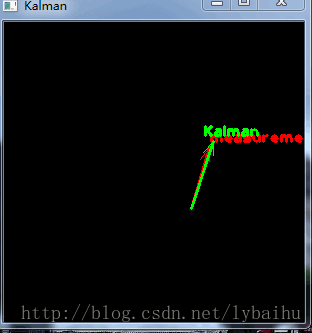
参考资料:
卡尔曼滤波器OpenCV自带例子
教程
卡尔曼滤波的直觉理解