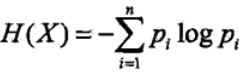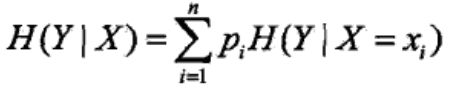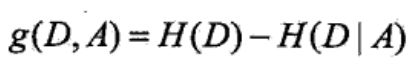决策树
通常决策树的学习分为3个步骤:特征选择、决策树的生成、决策树的剪枝。
一、特征选择
首先,看一组数据,是贷款申请样本数据表,年龄,有工作,有自己的房子,信贷情况为特征,类别为是否申请成功数据。摘自李航的统计机器学习。
决策树的本质是树,对应上面具体的问题,构建树的时候,选择年龄、有工作、有自己的房子、信贷情况、他们中谁作为二叉树的第一个节点会让分类的结果准确一点。就产生了决策树的特征选择问题。ID3算法、C4.5算法、CART算法对于分类问题的区别就是特征选择的不同,ID3算法采用信息增益,C4.5算法采用信息增益比,CART算法采用基尼系数。
1.1信息增益
在介绍信息增益之前,需要了解两个概念,一个是熵,一个是条件熵。熵衡量的是随机变量不确定性的度量。
设X是有限个值的离散随机变量,其概率分布为:
随机变量的熵定义为:
熵越大,则随机变量的不确定性越大。
以二分类来理解熵,用投硬币为例,投一枚硬币,是正面的概率是0.5,这个时候,投出的硬币是正面还是反面的不确定性最大。而这个时候恰好熵最大为1.
条件熵表示的是在已知随机变量X的条件下随机变量Y的不确定性。
信息增益是熵与条件熵的差值
下图举了一个如何计算信息增益的例子:
信息熵容易选择取值比较多的特征,例如,以上表中的Id做为特征,对于所有的特征来说,熵都一样,条件经验熵越小,信息增益越大,越容易被选为特征。当以ID做为特征时,一共可以分成14个类别,每个类别计算的时候值都为0,这时信息增益最大。但ID作为分类依据明显没有太大的意义,所以引入了信息增益比。
1.2信息增益比
下面是信息增益比的定义:
还是以刚才的ID为例,计算ID的信息增益比时,先计算出信息增益,然后计算ID的熵,ID的取值一共有14个类别,每个类别的概率为1/14.所以ID的熵为-14*1/14*log(1/14)(因为有14个类别,要累加求和,所以这里乘了14)。这样信息增益比就可以解决信息增益率选择取值多的特征,但是信息增益比容易选择取值少的特征。所以有了后面的基尼系数。
1.3基尼系数
二、决策树的生成
下面以ID3为例,讲解如何构造决策树,代码来自机器学习实战中的代码:
from math import log
def createDataSet():
"""
样本包括5个海洋动物,特征包括:不浮出水面是否可以生存,是否有脚蹼
类别为:是否是鱼类
"""
dataSet = [[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']
]
labels = ['no surfacing','flippers']
return dataSet,labels
def calShannonEnt(dataSet):
"""
计算样本的熵
"""
#统计样本数量
numEntries = len(dataSet)
labelCounts = {}
#统计出每一个类别有多少样本
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
#计算出每个类别的熵,并求和
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob*log(prob,2)
return shannonEnt
def splitDataSet(dataSet,axis,value):
"""
划分子集,axis是特征,value是特征值
找到指定特征的值,将其去掉,为了方便计算子集的信息熵
"""
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
def chooseBestFeatureToSplit(dataSet):
"""
根据信息增益计算最好的特征
"""
#计算特征的个数和计算样本信息熵
numFeatures = len(dataSet[0]) - 1
baseEntropy = calShannonEnt(dataSet)
bestInfoGain = 0
bestFeature = -1
#遍历所有特征,计算信息增益,找到最好的特征
for i in range(numFeatures):
#找到第i个特征的取值,
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
#计算条件熵
for value in uniqueVals:
subDataSet = splitDataSet(dataSet,i,value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob*calShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if(infoGain>bestInfoGain):
bestInfoGain = infoGain
bestFeature=i
return bestFeature
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():classCount[vote]=0
classCount[vote]+=1
sortedClassCount = sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
myDat,labels = createDataSet()
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
#当子集中所有的类别都相同的时候,结束递归,返回当前的特征
if classList.count(classList[0])==len(classList):
return classList[0]
#当特征为0的时候,返回其类别中最大的特征
if len(dataSet[0]) == 1:
print(classList)
return majorityCnt(classList)
#计算信息增益,划分特征
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat])
#找到最好特征的取值
featValues = [example[bestFeat] for example in dataSet]
uniquevals = set(featValues)
#根据取值,把数据分成不同的集合,递归构造树
for value in uniquevals:
subLabels = labels[:]
myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
return myTree
tree=createTree(myDat,labels)下面是输出的结果:
三、决策树的剪枝
剪枝是决策树学习过程中处理过拟合的方法,剪枝分为预剪枝和后剪枝。预剪枝是在生成过程中,对节点进行估计,如果当前划分不能提升系统的泛化能力,则停止分割。后剪枝是先生成一颗完整的树,自底向上对非叶节点进行考察,如果该叶节点替换成的子树能带来泛化性能的提升,则用该节点替换为叶节点。
参考资料:1>李航统计机器学习
2>西瓜书
3>机器学习实战