机器学习——线性回归
文章目录
- 什么是线性回归
- 如何衡量 Yi' 与 Yi 的差别
- 一元线性回归模型
- 多元线性回归模型
- 线性回归的基本用途
- 线性回归的优缺点
- 线性回归的拓展
- 线性回归的使用条件
什么是线性回归
引用维基百科对线性回归的定义:
线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个
自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的
模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归
举个例子
现有一系列自变量与因变量的对应关系对:
(x11,x12,…,x1d,Y1),(x21,x22,…,x2d,Y2),…,(xm1,xm2,…,xmd,Ym)
线性回归试图通过自变量的线性组合来趋近因变量,即:
Yi’=w1xi1+w2xi2+…wnxid+b,使得 Yi’ 趋近于 Yi , 从代数角度来看,线性回归试图确定 (w1,w2,…,wd,b) ,使得Yi’ 趋近于 Yi
如何衡量 Yi’ 与 Yi 的差别
线性回归一般通过均方误差来度量Yi’ 与 Yi 之间的差别:
显然,线性回归的任务就是最小化均方误差,即模型输出的值与实际值之间的误差之和最小,基于均方误差最小化来进行模型求解的方法称为”最小二乘法“
一元线性回归模型
在讲解多元线性回归之前,先来看看一元线性回归,一元线性回归试图学得:Yi’=wxi+b,使得Yi’ 趋近于 Yi,我们可以通过最小二乘法求解出w 与 b
对于一元线性回归模型,均方误差变为:
这个函数具有一个特点,其Hessian矩阵半正定,即E为凸函数
凸函数最低点沿各坐标轴方向的斜率为0,对2.1求偏导得:
[外链图片转存失败(img-2EE7baWg-1564282832468)(https://i.imgur.com/SyVjpXT.png)]
令式子(2.2)、(2.3)等于0可得:
[外链图片转存失败(img-FOJBcMLQ-1564282832469)(https://i.imgur.com/R146XqI.png)]
多元线性回归模型
多元线性模型即本文开头所举的例子,令Xi=(xi1,xi2,…,xid,1),W=(w1,w2,…,wd,b),多元线性回归试图学得:
[外链图片转存失败(img-2VJA5Z1r-1564282832469)(https://i.imgur.com/CMRVvW4.png)]
使得Yi’ 趋近于 Yi
在多元线性规划问题中,均方误差公式变为:
[外链图片转存失败(img-TPboKk1r-1564282832469)(https://i.imgur.com/FJGprcs.png)]
其Hessian矩阵仍然半正定,所以式2.4仍为一个凸函数,现考虑如何求得W
只需令(2.5)的所有式子为0,求解出的W即为最优解(凸函数最低点的所有一阶偏导数均为0),(2.5)等价于矩阵:
[外链图片转存失败(img-abvWDBgV-1564282832470)(https://i.imgur.com/lxDEbau.png)]
矩阵(2.0)等价于:
[外链图片转存失败(img-6QcWTbDn-1564282832470)(https://i.imgur.com/DWci8xB.png)]
[外链图片转存失败(img-SRJn2pyh-1564282832470)(https://i.imgur.com/2yMlSEW.png)]
因此,(2.5)的所有式子等于0等价于式子(2.6)等于0,令式子(2.6)等于0可得:
[外链图片转存失败(img-DFN7KsY4-1564282832471)(https://i.imgur.com/A0AHV3T.png)]
在现实情况中,XTX往往不是满秩矩阵,此时可以考虑使用梯度下降法或是牛顿法求得均方误差(式(2.4))的最优解
线性回归的基本用途
引用维基百科线性回归:
1、如果目标是预测或者映射,线性回归可以用来对观测数据集的和X的值拟合出一个预测模型。当完成
这样一个模型以后,对于一个新增的X值,在没有给定与它相配对的y的情况下,可以用这个拟合过的模型预测出一个y值。
2、给定一个变量y和一些变量X1,X2,…,Xn,这些变量有可能与Y相关,线性回归分析可以用来量化 Y 与 Xj 之间相关性的强度,评估出与Y不相关的Xj,并识别出哪些 Xj 的子集包含了关于Y的冗余信息。
其实线性回归也可以用来看事物发展的趋势,通过直线斜率便可以判断总体来说,事物是向上还是向下发展的
线性回归的优缺点
优点:解释性好,实现简单
缺点:对于异常值敏感,如果是离散值,例如因变量的取值为0、1,此时就无法使用线性回归
线性回归的拓展
上述讲解的线性回归是用一条直线去拟合数据,当然,我们也可以对上述线性回归的公式进行改进,用一条曲线去拟合数据:
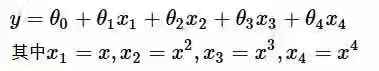
线性回归的使用条件
引自维基百科良哥最帅
1、样本是在总体之中随机抽取出来的。
2、因变量Y在实直线上是连续的,
3、残差项是独立且相同分布的(iid),也就是说,残差是独立随机的,且服从高斯分布
残差是指预测值与实际值之间的差距,高斯分布就是正态分布,这些假设可以推出为什么线性回归使用最小二乘法
我们设观测输出与预估数据之间的误差为:
ε i = Y i , − Y i ε_i=Y_i^,−Y_i εi=Yi,−Yi
以下内容整合自我是链接

则最大化对数似然等价于最小化 ∑ i = 0 m ε i 2 = ∑ i = 0 m ( Y i , − Y i ) 2 \sum_{i=0}^mε_i^2=\sum_{i=0}^m(Y_i^,−Y_i)^2 ∑i=0mεi2=∑i=0m(Yi,−Yi)2,其实就是最小化均方误差
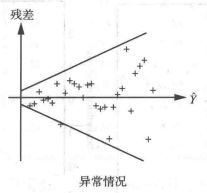
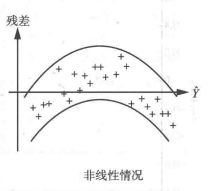
条件一与条件二是比较好满足的,条件三只要求残差近似满足正态分布即可,那么如何判断残差是否满足正态分布呢?答案是残差图,以下内容摘自IBM智库
“残差图”以回归方程的自变量为横坐标,以残差为纵坐标,将每一个自变量的残差描在该平面坐标上所形成的图形。当描绘的点围绕残差等于0的直线上下随机散布,说明回归直线对原观测值的拟合情况良好。否则,说明回归直线对原观测值的拟合不理想。
以下三个图来自百度百科,可以将自己的拟合结果与下列三幅图做对比,进行对号入座
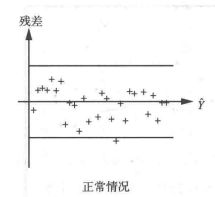
对于第一张图的情况,满足模型的各假设条件;对于第二张图的情况,表示回归值的大小与残差的波动大小有关系,即等方差性(我的理解是残差没有同分布)的假设有问题;对于第三张图,表示线性模型不合适的样本,可能有异常值存在。
对于第一张图,如果大部分点都落在横线画的中间部分,而只有少数几个点落在外边,则这些点对应的样本,可能有异常值存在。
同时,线性回归训练完毕后,往往要进行F检验、T检验、查看回归系数 R 2 R^2 R2,线性回归不能很好得处理多重共线性得情况