机器学习——拉格朗日插值与牛顿插值
以下内容均为个人理解,如有错误,欢迎指出
文章目录
- 什么是插值
- 预备知识
- 拉格朗日插值法
- 牛顿插值法
- 牛顿插值法与拉格朗日插值法的应用
- 参考文献
什么是插值
摘自百度百科
在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点
本节博客介绍拉格朗日插值法与牛顿插值法
预备知识
- 对于一个二维平面上的离散点,若其满足函数的定义,即一个x,只对应一个y,则可以唯一确定一个多项式函数
为了证明上述结论,我们需要证明这个多项式函数的存在性与唯一性,设n次多项式函数为 y = a n x n + a n − 1 x n − 1 + . . . . + a 0 y=a_nx^n+a_{n-1}x^{n-1}+....+a_0 y=anxn+an−1xn−1+....+a0,平面上存在n个不同的离散的点,记为 ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) (x_1,y_1),(x_2,y_2),...,(x_n,y_n) (x1,y1),(x2,y2),...,(xn,yn),这n个点满足函数的定义,则有: y 1 = a n x 1 n + a n − 1 x 1 n − 1 + . . . . + a 0 y 2 = a n x 2 n + a n − 1 x 2 n − 1 + . . . . + a 0 . . . . . . y n = a n x n n + a n − 1 x n n − 1 + . . . . + a 0 y_1=a_nx_1^n+a_{n-1}x_1^{n-1}+....+a_0\\ y_2=a_nx_2^n+a_{n-1}x_2^{n-1}+....+a_0\\ ......\\ y_n=a_nx_n^n+a_{n-1}x_n^{n-1}+....+a_0 y1=anx1n+an−1x1n−1+....+a0y2=anx2n+an−1x2n−1+....+a0......yn=anxnn+an−1xnn−1+....+a0
用矩阵表示上述所有式子得
[ y 1 y 2 . . y n ] = [ 1 x 1 x 1 2 . . . x 1 n 1 x 2 x 1 2 . . . x 2 n . . . . 1 x 1 x 1 2 . . . x n n ] ∗ [ a 0 a 1 . . . . a n ] ( 式 1.1 ) \begin{bmatrix} y_1\\ y_2\\ .\\ .\\ y_n \end{bmatrix} =\begin{bmatrix} 1 \ x_1 \ x_1^{2}...\ x_1^{n}\\\\ 1 \ x_2 \ x_1^{2}...\ x_2^{n}\\ ....\\ 1 \ x_1 \ x_1^{2}\ ...\ x_n^{n}\\ \end{bmatrix}* \begin{bmatrix} a_0\\ a_1\\ ....\\ a_n \end{bmatrix}(式1.1) ⎣⎢⎢⎢⎢⎡y1y2..yn⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡1 x1 x12... x1n1 x2 x12... x2n....1 x1 x12 ... xnn⎦⎥⎥⎥⎥⎤∗⎣⎢⎢⎡a0a1....an⎦⎥⎥⎤(式1.1)
令 A = [ 1 x 1 x 1 2 . . . x 1 n 1 x 2 x 1 2 . . . x 2 n . . . . 1 x 1 x 1 2 . . . x n n ] , X = [ a 0 a 1 . . . . a n ] , Y = [ y 1 y 2 . . y n ] A=\begin{bmatrix} 1 \ x_1 \ x_1^{2}...\ x_1^{n}\\\\ 1 \ x_2 \ x_1^{2}...\ x_2^{n}\\ ....\\ 1 \ x_1 \ x_1^{2}...\ x_n^{n}\\ \end{bmatrix},X=\begin{bmatrix} a_0\\ a_1\\ ....\\ a_n \end{bmatrix},Y=\begin{bmatrix} y_1\\ y_2\\ .\\ .\\ y_n \end{bmatrix} A=⎣⎢⎢⎢⎢⎡1 x1 x12... x1n1 x2 x12... x2n....1 x1 x12... xnn⎦⎥⎥⎥⎥⎤,X=⎣⎢⎢⎡a0a1....an⎦⎥⎥⎤,Y=⎣⎢⎢⎢⎢⎡y1y2..yn⎦⎥⎥⎥⎥⎤
则有 A X = Y AX=Y AX=Y,只需求出 X X X,过这n个点的多项式就求出来了, A A A是著名的范德蒙矩阵,当 x i , 1 ≤ i ≤ n x_i,1 \leq i \leq n xi,1≤i≤n两两不相等时,其行列式不等于0,意味着给定 Y Y Y, X X X具有唯一解,由此可知,二维平面上过所有已知点的多项式函数有且仅有一个
有了上述结论,我们来想一想应该如何求解式1.1,我们只需要构造一个n次多项式,使得这个多项式在 x = x n x=x_n x=xn时, y = y n y=y_n y=yn即可,拉格朗日和牛顿从两个不同的角度解决了这个问题,这两个方法构造的多项式函数都是相同的
拉格朗日插值法
拉格朗日构造的n次多项式如下:
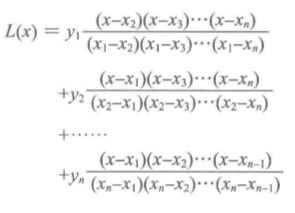
注意上式满足 L ( x 1 ) = y 1 , L ( x 2 ) = y 2 , . . . . . , L ( x n ) = y n L(x_1)=y_1,L(x_2)=y_2,.....,L(x_n)=y_n L(x1)=y1,L(x2)=y2,.....,L(xn)=yn
拉格朗日插值法固然简单,但是每当出现新的离散点时,整个多项式都需要重新构造,为了解决这个问题,我们有了牛顿插值法
牛顿插值法
拉格朗日插值法是从已知的全部点出发,求得多项式函数的,因此当出现多的点时,需要重新计算一遍,那我们可不可以用递推的方式来构造多项式呢?即已知过n-1个点的多项式函数,在此基础上对其进行更改,使其过第n个点,由此一来,当出现多的点时,就不需要重新构造一遍多项式函数。这就是牛顿插值法的出发点。
那么问题就是如何在已知过n-1个点的多项式函数 f n − 1 ( x ) f_{n-1}(x) fn−1(x)的基础上,构造出过n个点的多项式函数表达式,牛顿给出的答案是: f n ( x ) = f n − 1 ( x ) + b n ( x − x 1 ) ( x − x 2 ) . . . . ( x − x n − 1 ) ( 式 1.2 ) f_n(x)=f_{n-1}(x)+b_n(x-x_1)(x-x_2)....(x-x_{n-1})(式1.2) fn(x)=fn−1(x)+bn(x−x1)(x−x2)....(x−xn−1)(式1.2)
注意上式,当 x = x i x=x_i x=xi , 1 ≤ i ≤ n − 1 1 \leq i \leq n-1 1≤i≤n−1, f n ( x i ) = f n − 1 ( x i ) = y i f_n(x_i)=f_{n-1}(x_i)=y_i fn(xi)=fn−1(xi)=yi (由于多项式函数 f n − 1 ( x ) f_{n-1}(x) fn−1(x)过前n-1个点)
那么现在的问题是如何求解 b n b_n bn,这个简单,只需要将第n个点代入其中即可求解,那么 b n b_n bn解的形式有没有什么规律呢?幸运的是,在式1.2的形式下, b n b_n bn的解可以表示n阶均差的形式,即 f [ x n , x n − 1 , . . . . . , x 1 ] = f [ x n , x n − 1 , . . . . . , x 2 ] − f [ x n − 1 , . . . . . , x 1 ] x n − x 1 f[x_n,x_{n-1},.....,x_1]=\frac{f[x_n,x_{n-1},.....,x_2]-f[x_{n-1},.....,x_1]}{x_n-x_1} f[xn,xn−1,.....,x1]=xn−x1f[xn,xn−1,.....,x2]−f[xn−1,.....,x1]
而n阶均差可以通过递推的方式求得,例如当n=5时,有:
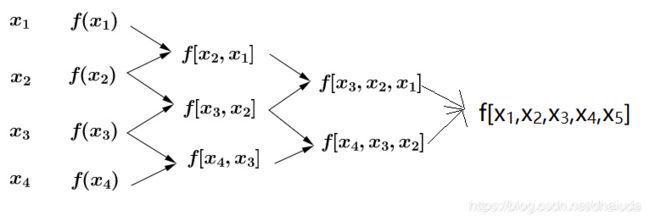
一阶均差可以直接求得,例如 f [ x 2 , x 1 ] = f ( x 2 ) − f ( x 1 ) x 2 − x 1 f[x_2,x_1]=\frac{f(x_2)-f(x_1)}{x_2-x_1} f[x2,x1]=x2−x1f(x2)−f(x1)
对式1.2进行展开,我们得到牛顿插值法的表现形式

当出现新的点 ( x n + 1 , f ( x n + 1 ) ) (x_{n+1},f(x_{n+1})) (xn+1,f(xn+1))时,只需要通过上面描述的阶差的递推方式求出 b n + 1 b_{n+1} bn+1即可获得过这n+1个点的多项式函数,例如我们以有过四个点的多项式函数,现在多出一个点 ( x 5 , f ( x 5 ) ) (x_5,f(x_5)) (x5,f(x5)),我们通过下列方式求 b 5 b_5 b5: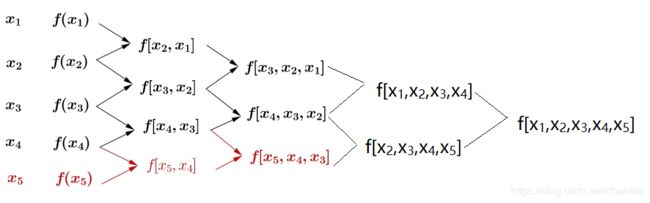
根据式1.2便可求得过这5个点的多项式函数
牛顿插值法与拉格朗日插值法的应用
牛顿插值法与拉格朗日插值法可以用于缺失值的填充
参考文献
1、维基百科插值
2、牛顿插值的几何解释是怎么样
3、如何直观地理解拉格朗日插值法?