机器学习——SVM预备知识 拉格朗日乘子法的推导

---

以下内容仅供参考，如有错误，欢迎指出

---

什么是拉格朗日乘子法

以下内容摘自周志华老师的《机器学习》

拉格朗日乘子法是一种寻找多元函数在一组约束条件下的极值的方法，通过引入拉格朗日乘子，可将有d个变量与k个约束条件的最优化问题转换为具有d+k个变量的无约束优化问题求解

预备知识——水平集

以下内容摘自安全学求过

在数学领域中, 一个具有n变量的实值函数f的水平集是具有以下形式的集合
$\{(x_1,...,x_n)|f(x_1,...,x_n)=c\}$
其中 c 是常数. 水平集即使得函数值具有给定常数的变量集合.
当具有两个自变量时, 称为水平曲线(等高线), 如果有三个自变量, 称为水平曲面, 更多自变量时, 水平集被叫做水平超曲面.

只具有一个等式约束的凸函数最优化问题

本节暂时只讨论求解满足等式约束条件下，凸函数最小的情况，但其求解方法同样适用于使目标函数最大的情况。

问题描述

假定x为d维向量，欲寻找x的某个取值$x^{\ast }$，使凸函数$f(x)$最小并满足$g(x^{\ast })=c$，c为常数，即：
$$\begin{gathered} \underset{x}{\min }f(x) \\ s.tg(x)=c \end{gathered}$$

问题的解决方案

使用拉格朗日乘子法,具体步骤如下

• 定义拉格朗日函数$L(x,\lambda )=f(x)+\lambda (g(x)-c)(\lambda !=0)(式1.0)$
• 计算$$\{\begin{array}{r}\frac{\partial L(x,\lambda )}{\partial x}=0\\ \frac{\partial L(x,\lambda )}{\partial \lambda }=0\end{array}$$
  d+1个变量(x是d维向量，有d个变量，加上一个$\lambda$)，d+1个方程，一定可以进行求解，求解出的$x$代入$f(x)$

拉格朗日乘子法为什么有效的简单推导

为便于理解，我们在三维函数上进行讨论，即利用拉格朗日乘子法解决以下凸优化问题：
$$\begin{gathered} \underset{x,y}{\min }f(x,y) \\ s.tg(x,y)=c \end{gathered}$$
我们在xOy平面上画出函数$f(x,y)$的等高线和函数$g(x,y)$的等高线（概念见预备知识一节中的水平集），接着，我们只保留函数$g(x,y)=c$时的等高线，结果如下图：

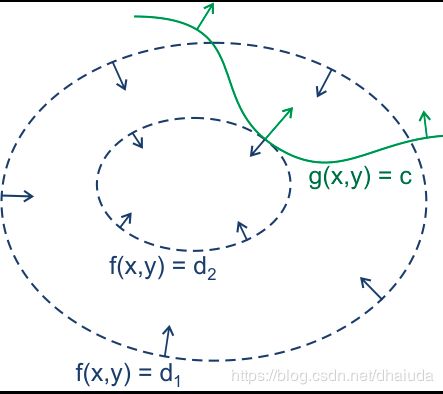
上图的蓝色箭头表示函数$f(x,y)$梯度的反方向，绿线表示函数$g(x,y)$的取值为c时的梯度方向，(x,y)只能位于绿线上，现在我们要求位于绿线上的点对应的$f(x,y)$的最小值，我们来思考一下

• 这里先理解一下登高线形成的圈有什么含义，对于凸函数来说，等高线形成的圈越小，则离全局最小越接近，现在我们有一个想法，$g(x,y)=c$的等高线与函数$f(x,y)$的若干等高线有若干交点，每个交点所处的等高线围成的圈大小不同，圈越小，对应的$f(x,y)$取值越小，那么只需要找到圈最小处的交点，不就是函数$f(x,y)$在$g(x,y)=c$约束下的最小值了吗？

• 那么圈最小处的交点有什么特性呢？注意到圈最小，意味着该圈内部的圈不可能在与函数$g(x,y)=c$的登高线具有交点，否则这个圈就不是最小了，因为外层的圈肯定比内层的圈要大，这意味圈最小处的交点位于的等高线与函数$g(x,y)=c$相切

• 相切意味着什么？这里有一个定理——梯度与登高线的切线垂直，证明请查看为什么梯度的方向与等高线切线方向垂直
  由此可知，相切意味着两个函数的梯度共线，即存在常数$\lambda$满足$\nabla f(x,y)=\lambda \nabla g(x,y)$，即$\nabla f(x,y)-\lambda \nabla (g(x,y)-c)=0$(为什么要减c下面解释)，将负号统一到$\lambda$中即得到$\nabla f(x,y)+\lambda \nabla (g(x,y)-c)=0$，即函数$L(x,y,\lambda )=f(x,y)+\lambda (g(x,y)-c)$（式1.1）对x，y求偏导，故有
  $$\begin{gathered} \frac{\partial f(x,y)}{\partial x}+\lambda \frac{\partial (g(x,y)-c)}{\partial x}=0 \\ \frac{\partial f(x,y)}{\partial y}+\lambda \frac{\partial (g(x,y)-c)}{\partial y}=0 \end{gathered}$$
  式1.1具有三个变量，但是只有两个方程，我们还差一个方程，不怕不怕，式1.1对$\lambda$求导，即得到约束条件，与上述两个方程联立，此时即可求解出x、y、$\lambda$。

• 式1.1之所以多减去一个c，是为了让式1.1对$\lambda$求导置0得到约束条件，将相切的点限制在$g(x,y)=c$中（$g(x,y)$与$f(x,y)$等高线相切的点有很多），此时将约束问题统一为对式1.0的无约束问题（只需将式1.0对$x、y、\lambda$求导即可）

值得注意的是，相切处并不一定就是最小值，也有可能是最大值，即函数等高线形成的圈内部相切于约束等高线，因此我们需要将求得的多个相切值代入原式，从而取最小

只具有一个不等式约束的凸函数最优化问题

问题描述

假定x为d维向量，欲寻找x的某个取值$x^{\ast }$，使凸函数$f(x)$最小并满足$g(x^{\ast })\le 0$，即：
$$\begin{gathered} \underset{x}{\min }f(x) \\ s.th(x)\le 0 \end{gathered}$$

问题的解决方案

使用拉格朗日乘子法,具体步骤如下

• 定义拉格朗日函数$L(x,\lambda )=f(x)+\lambda h(x)(\lambda !=0)(式1.2)$
• 计算$$\{\begin{array}{r}\frac{\partial L(x,\lambda )}{\partial x}=0\\ \frac{\partial L(x,\lambda )}{\partial \lambda }=0\end{array}$$
• 求出的$x、y、\lambda$需要满足KKT条件，否则不是原问题的解，KKT条件即为$$\{\begin{array}{rl}& h(x)\le 0\\ & \lambda \ge 0\\ & \lambda h(x)=0\end{array}$$
  上述过程在多维凸函数的多不等式约束求极值问题中依然能够成立

拉格朗日乘子法为什么有效的简单推导

考虑不等式约束$h(x)$，我们分两种情况讨论

1. 凸函数的极值位于$h(x)<0$处，此时不等式约束根本不起作用，即式1.2的$\lambda =0$，直接求解$\nabla f(x)=0$即可
2. 凸函数的极值不位于$h(x)<0$处，如下图(阴影部分表示$h(x)<0$，箭头表示梯度的逆方向)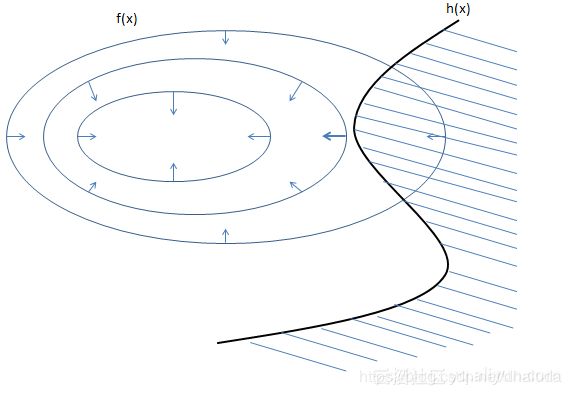：此时变为凸函数在$h(x)=0$下的极值问题，但此时有一个隐含条件 —— $f(x)$与$h(x)$的梯度方向相反，意味着$\lambda >0$，理由如下：
   由于凸函数$f(x)$的极值不在$h(x)<0$处，$f(x)$在切点的梯度方向将指向上图阴影部分（因为最小值不在阴影部分内，对切点来说，意味着凸函数$f(x)$在阴影部分的点取值比不在阴影部分的点取值要大），而函数$h(x)$在切点处的梯度方向指向阴影外部，因为阴影内部的点满足$h(x)<0$，切点满足$h(x)=0$，而梯度指向增长最快的方向，则$h(x)$在切点的梯度方向指向外部

当$\lambda =0$时，为第一种情况，当$\lambda >0,g(x)=0$时，为第二种情况，以上两种情况综合起来，就是KKT条件，此时仍然有许多约束条件，我们可以使用拉格朗日对偶对其进行求解，请查看机器学习——SVM预备知识 拉格朗日对偶推导与证明

多等式约束与多不等式约束的凸函数最优化问题

问题描述

假定x为d维向量，欲寻找x的某个取值$x^{\ast }$，使凸函数$f(x)$最小并满足$g(x^{\ast })\le 0$，即：
$$\begin{gathered} \underset{x}{\min }f(x) \\ s.t{h}_i(x)\le 0（i=1,2,3....n） \\ {g}_j(x)=0（j=1,2.....m） \end{gathered}$$

问题的解决方案

将上两节的内容进行推广即可得到拉格朗日乘子法解决多等式约束与多不等式约束的凸函数最优化问题的形式
$$L(x,\lambda ,\mu )=f(x)+\sum _{i=1}^m{\mu }_i{g}_i(x)+\sum _{i=1}^n{\beta }_i{h}_i(x)$$
需满足
$$\{\begin{array}{rlr}& g_i(x)\le 0& i=1,2.....n\\ & {\mu }_i\ge 0& i=1,2.....n\\ & {\mu }_i{g}_i(x)=0& i=1,2.....n\\ & h_j(x)=0& j=1,2.....m\\ & \frac{\partial L(x_k,\mu ,\beta )}{\partial x_k}=0& k=1,2....d\end{array}$$
约束多的可怕，不怕不怕，通过拉格朗日对偶可以转换为非常简介的形式，请查看机器学习——SVM预备知识 拉格朗日对偶推导与证明