Opencv2.4学习::图像卷积
图像卷积
直观表示:
(这部分内容来自:https://blog.csdn.net/chaipp0607/article/details/72236892?locationNum=9&fps=1)
(原文中还有关于模糊、锐化、提取边缘的各种核的描述,通过卷积可以实现这些操作)
数字图像处理中卷积
数字图像是一个二维的离散信号,对数字图像做卷积操作其实就是利用卷积核(卷积模板)在图像上滑动,将图像点上的像素灰度值与对应的卷积核上的数值相乘,然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值,并最终滑动完所有图像的过程。 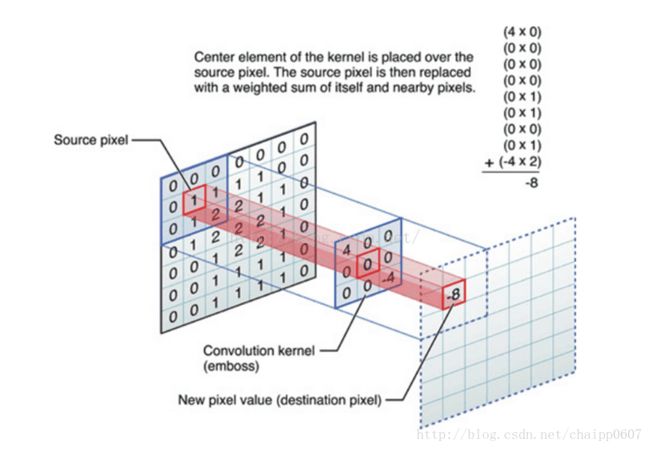
这张图可以清晰的表征出整个卷积过程中一次相乘后相加的结果:该图片选用3*3的卷积核,卷积核内共有九个数值,所以图片右上角公式中一共有九行,而每一行都是图像像素值与卷积核上数值相乘,最终结果-8代替了原图像中对应位置处的1。这样沿着图片一步长为1滑动,每一个滑动后都一次相乘再相加的工作,我们就可以得到最终的输出结果。除此之外,卷积核的选择有一些规则:
1)卷积核的大小一般是奇数,这样的话它是按照中间的像素点中心对称的,所以卷积核一般都是3x3,5x5或者7x7。有中心了,也有了半径的称呼,例如5x5大小的核的半径就是2。
2)卷积核所有的元素之和一般要等于1,这是为了原始图像的能量(亮度)守恒。其实也有卷积核元素相加不为1的情况,下面就会说到。
3)如果滤波器矩阵所有元素之和大于1,那么滤波后的图像就会比原图像更亮,反之,如果小于1,那么得到的图像就会变暗。如果和为0,图像不会变黑,但也会非常暗。
4)对于滤波后的结构,可能会出现负数或者大于255的数值。对这种情况,我们将他们直接截断到0和255之间即可。对于负数,也可以取绝对值。
再上张动图表示: 动图来自博客:https://blog.csdn.net/weixin_39124778/article/details/78411314
核心函数:
1.dft()
dft(),其定义如下:
C++: void dft(InputArray src, OutputArray dst, int flags=0, int nonzeroRows=0); 参数解释:
. InputArray src: 输入图像,可以是实数或虚数
. OutputArray dst: 输出图像,其大小和类型取决于第三个参数flags
. int flags = 0: 转换的标识符,有默认值0.其可取的值如下所示:
。DFT_INVERSE: 用一维或二维逆变换取代默认的正向变换
。DFT_SCALE: 缩放比例标识符,根据数据元素个数平均求出其缩放结果,如有N个元素,则输出结果以1/N缩放输出,常与DFT_INVERSE搭配使用。
。DFT_ROWS: 对输入矩阵的每行进行正向或反向的傅里叶变换;此标识符可在处理多种适量的的时候用于减小资源的开销,这些处理常常是三维或高维变换等复杂操作。
。DFT_COMPLEX_OUTPUT: 对一维或二维的实数数组进行正向变换,这样的结果虽然是复数阵列,但拥有复数的共轭对称性(CCS),可以以一个和原数组尺寸大小相同的实数数组进行填充,这是最快的选择也是函数默认的方法。你可能想要得到一个全尺寸的复数数组(像简单光谱分析等等),通过设置标志位可以使函数生成一个全尺寸的复数输出数组。
。DFT_REAL_OUTPUT: 对一维二维复数数组进行逆向变换,这样的结果通常是一个尺寸相同的复数矩阵,但是如果输入矩阵有复数的共轭对称性(比如是一个带有DFT_COMPLEX_OUTPUT标识符的正变换结果),便会输出实数矩阵。
. int nonzeroRows = 0: 当这个参数不为0,函数会假设只有输入数组(没有设置DFT_INVERSE)的第一行或第一个输出数组(设置了DFT_INVERSE)包含非零值。这样的话函数就可以对其他的行进行更高效的处理节省一些时间,这项技术尤其是在采用DFT计算矩阵卷积时非常有效。
2. getOptimalDFTSize()
返回给定向量尺寸经过DFT变换后结果的最优尺寸大小。其函数定义如下:
C++: int getOptimalDFTSize(int vecsize);参数解释:
int vecsize: 输入向量尺寸大小(vector size)
DFT变换在一个向量尺寸上不是一个单调函数,当计算两个数组卷积或对一个数组进行光学分析,它常常会用0扩充一些数组来得到稍微大点的数组以达到比原来数组计算更快的目的。一个尺寸是2阶指数(2,4,8,16,32…)的数组计算速度最快,一个数组尺寸是2、3、5的倍数(例如:300 = 5*5*3*2*2)同样有很高的处理效率。
getOptimalDFTSize()函数返回大于或等于vecsize的最小数值N,这样尺寸为N的向量进行DFT变换能得到更高的处理效率。在当前N通过p,q,r等一些整数得出N = 2^p*3^q*5^r.
这个函数不能直接用于DCT(离散余弦变换)最优尺寸的估计,可以通过getOptimalDFTSize((vecsize+1)/2)*2得到。
实现代码(卷积实现均值滤波):
代码中实现卷积的函数在创建Mat用了浅复制,参见矩阵的创建
#include
#include
#include
#include
using namespace std;
using namespace cv;
//图像卷积操作
void convolution(Mat src, Mat kernel, Mat &dst)
{
//输出图像定义 这里没有做边界补偿,
//所以输出图像比原图像小
dst.create(abs(src.rows - kernel.rows) + 1,
abs(src.cols - kernel.cols) + 1, src.type());
Size dftSize;
//计算傅立叶变换尺寸
dftSize.width = getOptimalDFTSize(src.cols +
kernel.cols - 1);
dftSize.height = getOptimalDFTSize(src.rows +
kernel.rows - 1);
//创建临时图像,初始化为0
Mat tempA(dftSize, src.type(), Scalar::all(0));
Mat tempB(dftSize, kernel.type(), Scalar::all(0));
//区域浅复制,roiA矩阵指向tempA,只是尺寸不一样
//因此,改变roiA,就是改变了tempA
Mat roiA(tempA, Rect(0, 0, src.cols, src.rows));
src.copyTo(roiA);
//imshow("temp", src);
Mat roiB(tempB, Rect(0, 0, kernel.cols, kernel.rows));
kernel.copyTo(roiB);
//傅立叶变换
dft(tempA, tempA, 0, src.rows);
dft(tempB, tempB, 0, kernel.rows);
//对频谱的每个元素进行乘法操作
mulSpectrums(tempA, tempB, tempA, DFT_COMPLEX_OUTPUT);
//取乘积后的逆变换
dft(tempA, tempA, DFT_INVERSE + DFT_SCALE, dst.rows);
//复制结果到输出图像
tempA(Rect(0, 0, dst.cols, dst.rows)).copyTo(dst);
}
void main()
{
Mat srcImage = imread("F:\\opencv_re_learn\\2.jpg");
if (!srcImage.data){
cout << "falied to read" << endl;
system("pause");
return;
}
cvtColor(srcImage, srcImage, CV_BGRA2GRAY);
//定义卷积核算子
Mat kernel = (Mat_(3, 3) << 1, 1, 1,
1, 1, 1,
1, 1, 1);
imshow("srcImage", srcImage);
srcImage.convertTo(srcImage, CV_32F);
Mat resultImage;
//卷积
convolution(srcImage, kernel, resultImage);
//归一化结果
normalize(resultImage, resultImage, 0, 1, CV_MINMAX);
imshow("resultImage", resultImage);
waitKey(0);
} 实现效果:


