在SRLID数据集上研究线性回归案例
说明
如何在动态劳动力收入动态调查上构建线性回归模型
操作
library(car)
data("SLID")
par(mfrow=c(2,2))
plot(SLID$wages ~ SLID$language)
plot(SLID$wages ~ SLID$age)
plot(SLID$wages ~ SLID$education)
plot(SLID$wages ~ SLID$sex)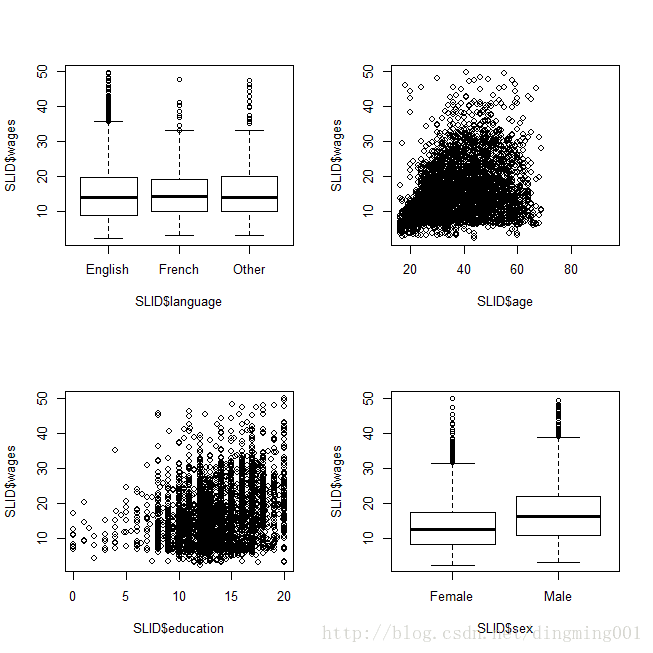
工资与多种影响因素之间关系
调用lm生成模型,summary( )查看
lmfit = lm(wages ~ . ,data = SLID)
summary(lmfit)
Call:
lm(formula = wages ~ ., data = SLID)
Residuals:
Min 1Q Median 3Q Max
-26.062 -4.347 -0.797 3.237 35.908
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.888779 0.612263 -12.885 <2e-16 ***
education 0.916614 0.034762 26.368 <2e-16 ***
age 0.255137 0.008714 29.278 <2e-16 ***
sexMale 3.455411 0.209195 16.518 <2e-16 ***
languageFrench -0.015223 0.426732 -0.036 0.972
languageOther 0.142605 0.325058 0.439 0.661
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.6 on 3981 degrees of freedom
(3438 observations deleted due to missingness)
Multiple R-squared: 0.2973, Adjusted R-squared: 0.2964
F-statistic: 336.8 on 5 and 3981 DF, p-value: < 2.2e-16languages属性不显著,去掉
lmfit = lm(wages ~ age + sex + education,data = SLID)
summary(lmfit)
Call:
lm(formula = wages ~ age + sex + education, data = SLID)
Residuals:
Min 1Q Median 3Q Max
-26.111 -4.328 -0.792 3.243 35.892
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.905243 0.607771 -13.01 <2e-16 ***
age 0.255101 0.008634 29.55 <2e-16 ***
sexMale 3.465251 0.208494 16.62 <2e-16 ***
education 0.918735 0.034514 26.62 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.602 on 4010 degrees of freedom
(3411 observations deleted due to missingness)
Multiple R-squared: 0.2972, Adjusted R-squared: 0.2967
F-statistic: 565.3 on 3 and 4010 DF, p-value: < 2.2e-16调用lmfit绘制函数诊断图
par(mfrow=c(2,2))
plot(lmfit)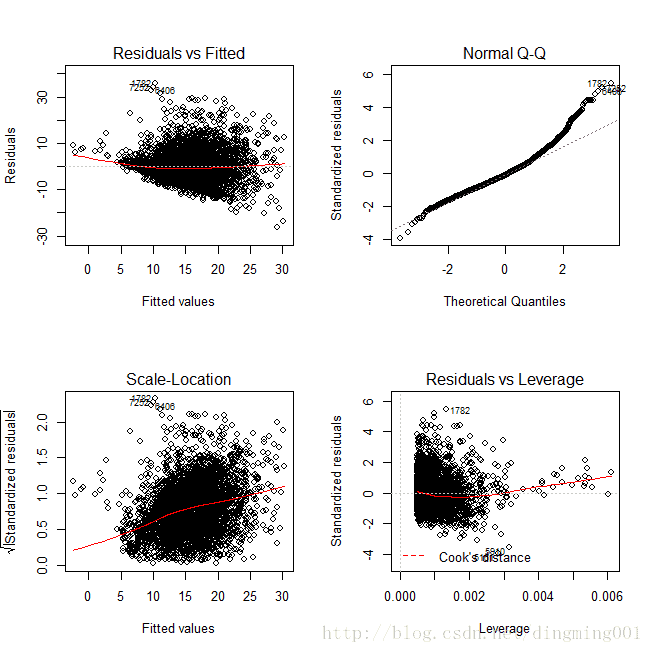
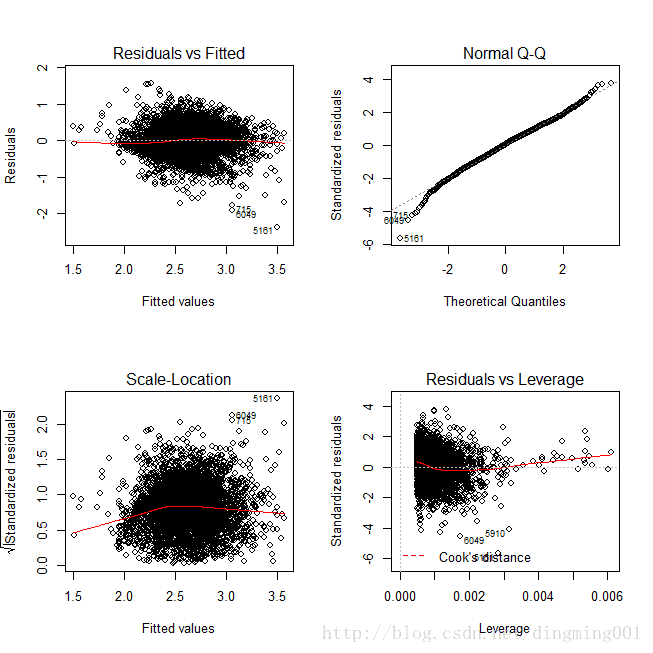
从残差图、位置尺度图可知,较小的残差相对回归模型存在一定的偏差。由于wages变化范围比较大,因此为了对称,引入wages的对数重新构建回归模型,调整后,代表残差的红色直线与位置-尺寸图都能更接近灰色虚线。
lmfit = lm(log(wages) ~ age + sex + education,data = SLID)
par(mfrow=c(2,2))
plot(lmfit)调用vif诊断多重共线性回归模型
vif(lmfit)
age sex education
1.011613 1.000834 1.012179
sqrt(vif(lmfit)) > 2
age sex education
FALSE FALSE FALSE 我们要验证函数中的变量是否存在多重共线性关系,我们调用vif函数计算线性与广义线性模型的方差膨胀因子与广义方差膨胀因子,如果多重共纯属存在,会发现预测值的膨胀因子大于2,然后去掉冗余的预测变量,或者使用主成分分析将预测变量集转化成一个不相关的小的变量集。
最后检测模型是否存在异方差性,用lmtest中的bptest判断异方差性.
library(zoo)
library(lmtest)
bptest(lmfit)
studentized Breusch-Pagan test
data: lmfit
BP = 29.031, df = 3, p-value = 2.206e-06
p值小于0.05,因此(不存在异方差的假设)不成立,存在异方差性,也就是说参数的标准误不正确。我们可以通过稳建标准差来修正标准误差,并不会去掉标准误。调用rms包的robcov函数来进一步提高那些正确的显著性强的参数的显著水平。
library(SparseM)
library(Hmisc)
library(lattice)
library(survival)
library(Formula)
library(rms)
olsfit = ols(log(wages) ~ age + sex + education,data = SLID,x = TRUE,y = TRUE)
robcov(olsfit)
Frequencies of Missing Values Due to Each Variable
log(wages) age sex education
3278 0 0 249
Linear Regression Model
ols(formula = log(wages) ~ age + sex + education, data = SLID,
x = TRUE, y = TRUE)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 4014 LR chi2 1486.08 R2 0.309
sigma0.4187 d.f. 3 R2 adj 0.309
d.f. 4010 Pr(> chi2) 0.0000 g 0.315
Residuals
Min 1Q Median 3Q Max
-2.36252 -0.27716 0.01428 0.28625 1.56588
Coef S.E. t Pr(>|t|)
Intercept 1.1169 0.0387 28.90 <0.0001
age 0.0176 0.0006 30.15 <0.0001
sex=Male 0.2244 0.0132 16.96 <0.0001
education 0.0552 0.0022 24.82 <0.0001 log(Y) = 1.1169 + 0.0176*X1 + 0.2244*X2 + 0.0552*X3