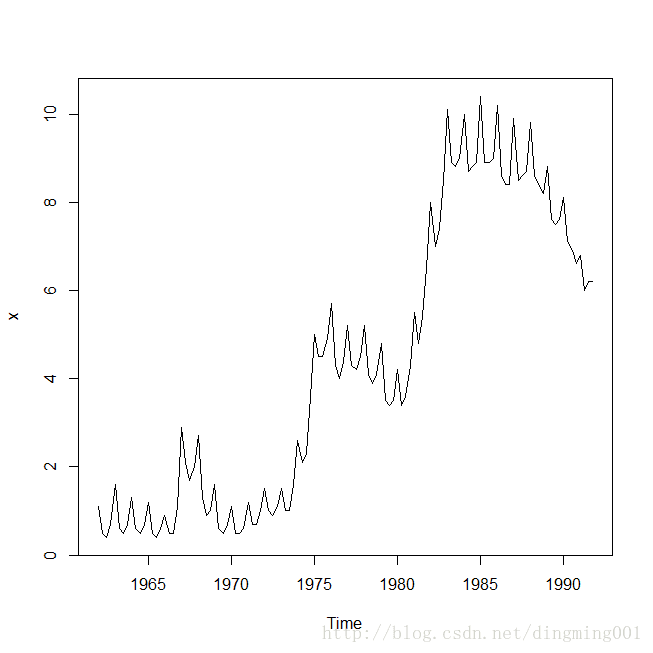ARIMA模型的季节模型
ARIMA模型可以对具有季节效应的序列建模，根据季节效应提取的难易程度可以分为简单季节模型与乘积季节模型。
简单季节模型
简单季节模型是指序列中的季节效应和其效应之间是加法关系
各种效应信息的提取都非常容易，通常简单的周期步长差分即可将序列中的季节信息提取充分，简单的低阶差分即可趋势信息提取充分，提取完季节信息和趋势信息之后的残差序列就是一个平稳序列，可以用ARMA模型拟合。
R语言中用arima函数中的seasonal选项拟合季节模型，相关命令如下 ：
arima(x,order=,include.mean=,method=,transform.pars=,fixed=,seasonal=)
-x:要进行模型拟合的序列命。
-order:指定模型阶数。
-include.mean:指定是否需要拟合常数项。
-method:指定参数估计方法。
-transform.pars:指定是否需要人为干预参数。
-fixed:对疏系数模型指定疏系数的位置。
-seasonal:指定季节模型的阶数与季节周期，该选项的命令格式为：
seasonal = list(order=c(P,D,Q),period = pi）
(1)加法模型：P=0,Q=0
(2)乘法模型：P,Q不全为零
拟合1962-1991年德国工人季度失业率序列
f<-read.table("D:/R-TT/book4/4R/data/file19.csv",sep=",",header = T)
x<-ts(f$unemployment_rate,start = c(1962,1),frequency = 4)
plot(x)
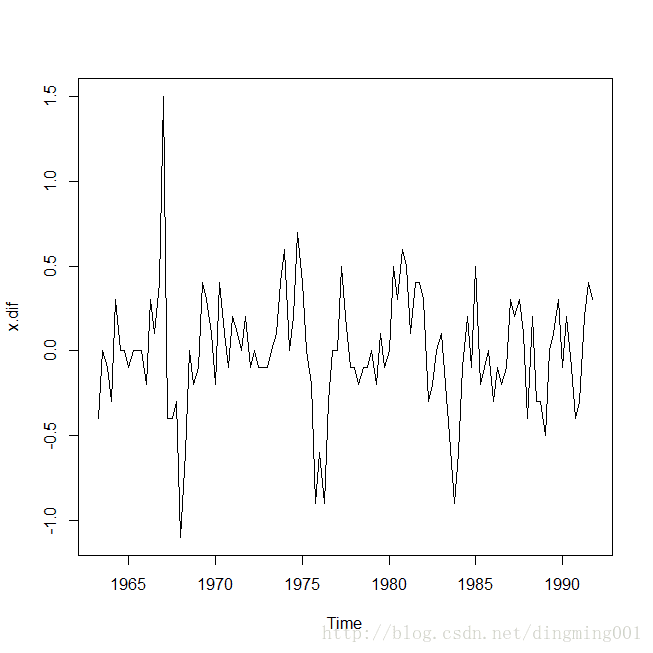
德国工人季节失业率序列时序图
#1阶4步差分，并绘制出差分后序列的时序图
x.dif<-diff(diff(x),4)
plot(x.dif)
差分后序列自相关图与偏自相关图
#绘制差分后序列自相关图和偏自相关图
acf(x.dif)
pacf(x.dif)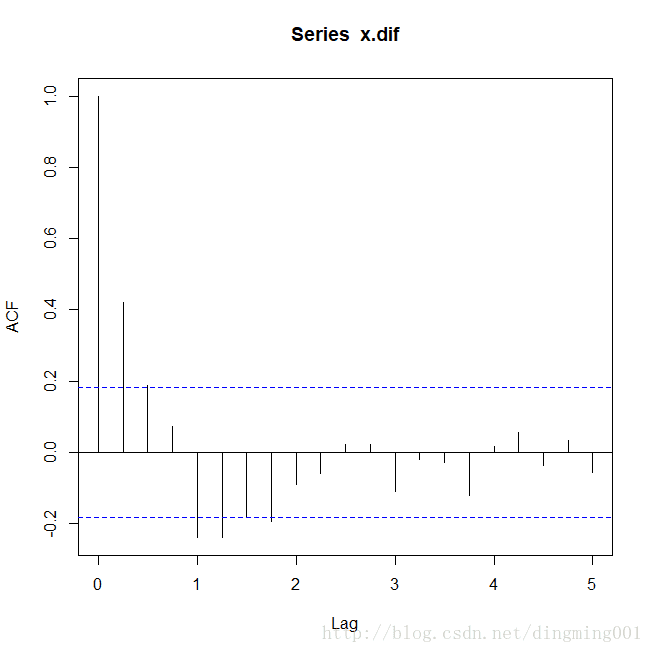
阶4步差分后序列自相关图
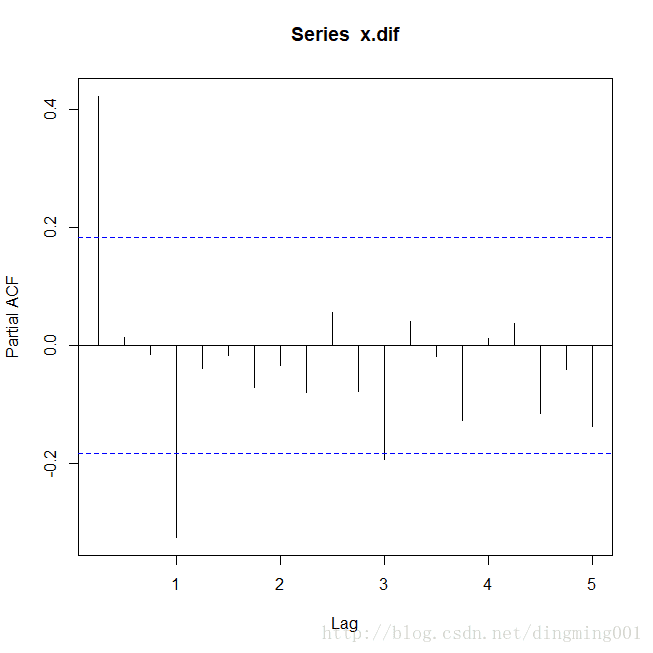
1阶4步差分后序列偏自相关图
自相关系数拖尾，而偏自相关系数1阶，4阶显著非零，4阶之后截尾。综合差分与自相关信息。拟合加法模型ARIMA((1,4)(1,4),0)
#拟合加法季节模型ARIMA((1,4),(1,4),0)
x.fit<-arima(x,order = c(4,1,0),seasonal = list(order=c(0,1,0),period=4,transform.par=F,fixed = c(NA,0,0,NA)))
x.fit
Call:
arima(x = x, order = c(4, 1, 0), seasonal = list(order = c(0, 1, 0), period = 4,
transform.par = F, fixed = c(NA, 0, 0, NA)))
Coefficients:
ar1 ar2 ar3 ar4
0.4143 0.0294 0.1257 -0.3300
s.e. 0.0879 0.0961 0.0952 0.0881
sigma^2 estimated as 0.09072: log likelihood = -25.51, aic = 61.02#残差白噪声检验
for(i in 1:2) print(Box.test(x.fit$residual,lag=6*i))
Box-Pierce test
data: x.fit$residual
X-squared = 0.54159, df = 6, p-value = 0.9973
Box-Pierce test
data: x.fit$residual
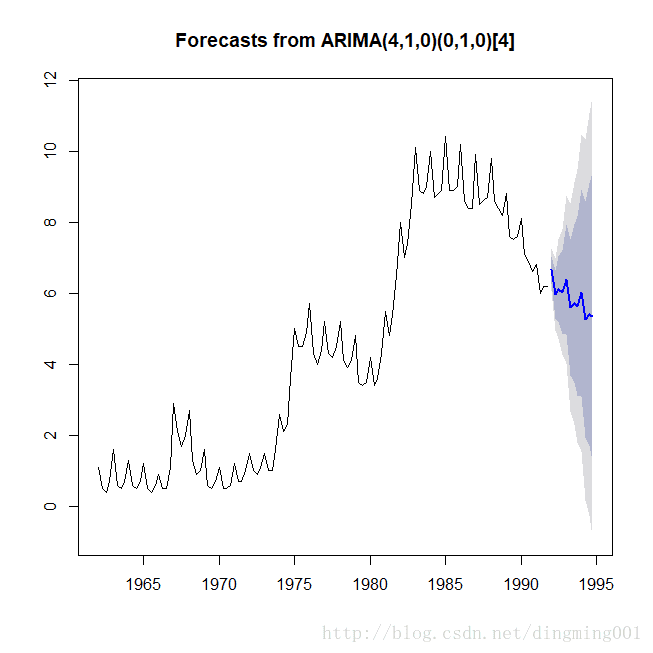
X-squared = 6.9427, df = 12, p-value = 0.8614做3年期预测
> library(forecast)
> x.fore<-forecast(x.fit,h=12)
> x.fore
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1992 Q1 6.660195 6.274201 7.046189 6.0698679 7.250522
1992 Q2 5.961087 5.292490 6.629683 4.9385564 6.983617
1992 Q3 6.116229 5.202010 7.030448 4.7180513 7.514406
1992 Q4 6.034304 4.877448 7.191161 4.2650446 7.803564
1993 Q1 6.386049 4.840267 7.931831 4.0219788 8.750119
1993 Q2 5.600664 3.694241 7.507088 2.6850413 8.516287
1993 Q3 5.721381 3.496132 7.946631 2.3181560 9.124607
1993 Q4 5.636065 3.119547 8.152583 1.7873832 9.484747
1994 Q1 6.010340 3.090620 8.930060 1.5450137 10.475666
1994 Q2 5.258337 1.937603 8.579071 0.1797120 10.336962
1994 Q3 5.404481 1.707100 9.101863 -0.2501751 11.059138
1994 Q4 5.334632 1.274994 9.394270 -0.8740483 11.543313绘图
plot(x.fore)
3年期12季度预测图
乘积季节模型
序列的季节效应、长期趋势效应和随机波动之间存在复杂的交互影响关系，简单的ARIMA模型不足以提取其中的相关关系，这时通常需要采用乘积季节模型。
拟合1948-1981年美国女性月度失业率序列
#读入数据，并绘制时序图
g<-read.table("D:/R-TT/book4/4R/data/file20.csv",sep=",",header = T)
x<-ts(g$unemployment_rate,start = c(1948,1),frequency = 12)
plot(x)
美国女性月度失业率时序图
#作1阶12步差分，并绘制出差分后序列的时序图
x.dif<-diff(diff(x),12)
plot(x.dif)
1阶12步差分时序图
#绘制差分后序列自相关图和偏自相关图
acf(x.dif)
pacf(x.dif)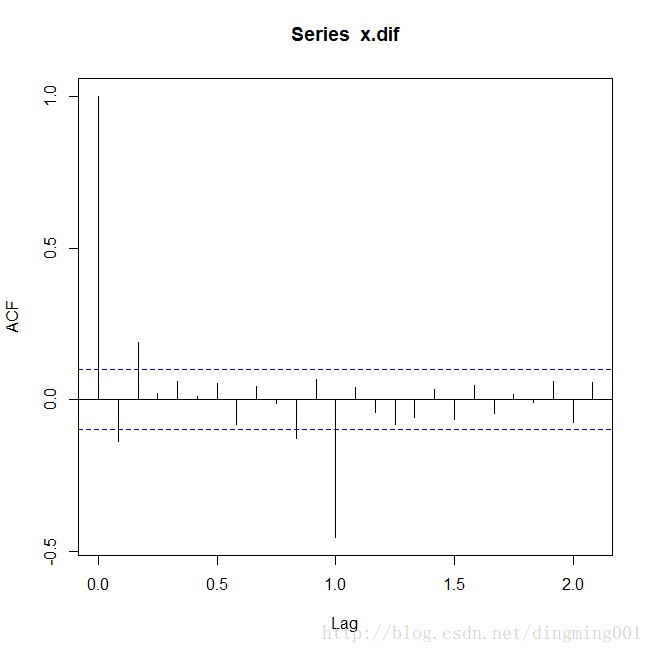
1阶12步差分自相关图
1阶12步差分偏自相关图
差分后序列的自相关图与偏自相关图都显示出拖尾属性，首先尝试拟合加法季节模型ARIMA(1,（1，12）,1)。然后进行残差序列的白噪声检测。
#拟合ARIMA(1,(1,12),1)模型
x.fit<-arima(x,order = c(1,1,1),seasonal = list(order=c(0,1,0),period=12))
for(i in 1:2) print(Box.test(x.fit$residual,lag=6*i))
Box-Pierce test
data: x.fit$residual
X-squared = 11.204, df = 6, p-value = 0.08228
Box-Pierce test
data: x.fit$residual
X-squared = 105.78, df = 12, p-value < 2.2e-16残差序列非白噪声，故模型拟合不正确
自相关系数延迟24阶后，截尾。
偏自相关系数延迟24阶后，仍拖尾。
这时以12步为周期的ARMA(0,1)12模型提取差分后序列季节自相关信息。
我们要拟合的乘积模型为 ARIMA(1,1,1)*(0,1,1)12
> #拟合ARIMA(1,1,1)*ARIMA(0,1,1)12模型
> x.fit<-arima(x,order = c(1,1,1),seasonal = list(order=c(0,1,1),period=12))
> x.fit
Call:
arima(x = x, order = c(1, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12))
Coefficients:
ar1 ma1 sma1
-0.7290 0.6059 -0.7918
s.e. 0.1497 0.1728 0.0337
sigma^2 estimated as 7444: log likelihood = -2327.14, aic =
4662.28残差序列白噪声检验
for(i in 1:2) print(Box.test(x.fit$residual,lag=6*i))
Box-Pierce test
data: x.fit$residual
X-squared = 4.5564, df = 6, p-value = 0.6018
Box-Pierce test
data: x.fit$residual
X-squared = 9.6288, df = 12, p-value = 0.6485
残差序列白噪声检验显示，该拟合模型显著成立。