深度强化学习研究笔记(3)——Deep Q-Network(DQN)(DQN问题引入,建模,一个Python小例子)
文章目录
- 1. 深度强化学习(Deep Q-Network,DQN)问题引入
- 2. 问题建模
- 3. 算法描述
- 4. DQN玩CartPole游戏示例
- 4.1 游戏接口定义
- 4.2 网络结构
- 4.3 网络训练
- 4.4 动作选择($\varepsilon$-greedy算法)
- 4.5 main函数
- 4.6 Putting It All Together(from Pinard)
- 5. 小结
1. 深度强化学习(Deep Q-Network,DQN)问题引入
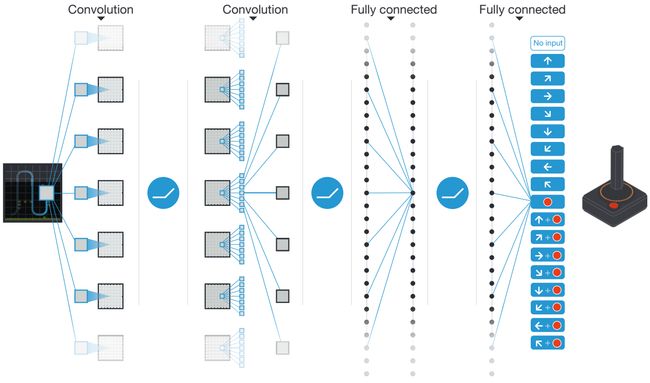
传统Q-learning方法难以处理真实场景下的高维数据,将大量的state和 Q Q Q value存储在内存中会导致计算复杂。于是有研究者想到利用深度神经网络(DNN)来高维数据的强化学习问题,其核心思想是利用价值函数的近似(Value Function Approximation)求解,通过深度神经网络来表示 Q Q Q值的近似分布。粗略地理解,可以认为利用深度神经网络(DNN)来代替Q-learning中的Q-table。下图描述了如何利用深度神经网络来进行强化学习(图片来源:Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., … & Petersen, S. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), 529. 在线阅读)
从某种意义上,我们可以将深度神经网络(DNN)视为一个黑盒子。拿强化学习代理玩游戏作为应用场景案例,DNN将游戏状态作为输入并返回每个动作的Q值近似值,之后我们选择具有最大Q值的动作——就像传统的Q-learning方法一样。 为了使我们的神经网络能够根据环境进行预测,我们必须为它们提供输入和输出对进行训练,神经网络将通过迭代地更新参数来训练该数据以基于输入来近似输出。
为什么玩电子游戏没办法直接用Q-learning 来学习最佳路径呢?因为电子游戏的每一帧图片就可以是一种状态,游戏中的角色又可以有多种动作(上下左右,下蹲跳跃等等)。如果用Q表来记录每一个动作所对应的状态,那么这张Q表将大到无法想象。
—— from AI学习笔记——深度Q-Learning(Deep Q-Learing(DQN))
2. 问题建模
首先,我们按照深度学习范式来构建损失函数,如下所示:
(1) L i ( θ i ) = E s , a ∼ ρ ( ⋅ ) [ ( y i − Q ( s , a ; θ i ) ) 2 ] L_i\left ( \theta_i \right )=\mathbb{E}_{s,a\sim \rho \left ( \cdot \right )}\left [ \left ( y_i-Q\left ( s,a;\theta_i \right ) \right ) ^{2} \right ] \tag {1} Li(θi)=Es,a∼ρ(⋅)[(yi−Q(s,a;θi))2](1)
其中, i i i表示迭代次数, θ i \theta_i θi表示第 i i i次迭代时的Q-network的网络权重。 ρ ( s , a ) \rho (s,a) ρ(s,a)是状态序列 s s s和动作 a a a的概率分布,我们将其称之为行为分布(behaviour distribution)。 Q ( s , a ; θ i ) Q\left ( s,a;\theta_i \right ) Q(s,a;θi)表示Q-network中通过神经网络来拟合的Q值函数,即 Q ( s , a ; θ ) ≈ Q ∗ ( s , a ) Q\left ( s,a;\theta \right ) \approx Q^*\left ( s,a \right ) Q(s,a;θ)≈Q∗(s,a)。 y i y_i yi表示第 i i i次迭代的目标 Q Q Q值(target Q Q Q):
(2) y i = E s ′ ∼ ε [ r + γ ⋅ max a ′ Q ( s ′ , a ′ ; θ i − 1 ) ∣ s , a ] y_i=\mathbb{E}_{s' \sim \varepsilon }\left [ r+\gamma \cdot \text{max}_{a'} Q\left ( s',a';\theta_{i-1} \right ) \mid s,a \right ] \tag {2} yi=Es′∼ε[r+γ⋅maxa′Q(s′,a′;θi−1)∣s,a](2)
和深度学习方法一致,在第 i i i次迭代计算损失值时,我们采用的是第 i − 1 i-1 i−1次迭代的网络权重。上述公式(2)中, r + γ ⋅ max a ′ Q ( s ′ , a ′ ; θ i − 1 ) r+\gamma \cdot \text{max}_{a'} Q\left ( s',a';\theta_{i-1} \right ) r+γ⋅maxa′Q(s′,a′;θi−1)表示目标 Q Q Q值(它通过以前的网络权重进行计算), Q ( s , a ) Q\left( {s,a} \right) Q(s,a)表示当前的 Q Q Q值(它通过当前最新的网络权重进行计算)。这里,我们可以回顾Q-learning算法中的 Q Q Q值更新公式(学习率设置为1):
(3) Q ( s t , a t ) ← Q ( s t + 1 , a t ) ← r t + λ ⋅ max a Q ( s t + 1 , a ) ← r t + γ ⋅ max a Q ( s t + 1 , a ) \begin{aligned} Q\left( {{s_t},{a_t}} \right) &\leftarrow Q\left( {{s_{t + 1}},{a_t}} \right) \\ &\leftarrow {r_t} + \lambda \cdot \mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right) \\ & \leftarrow {r_t} + \gamma \cdot \mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right) \end{aligned} \tag {3} Q(st,at)←Q(st+1,at)←rt+λ⋅amaxQ(st+1,a)←rt+γ⋅amaxQ(st+1,a)(3)
通过公式(3)能够佐证,公式(2)中的 ( r + γ ⋅ max a ′ Q ^ ( s , a ′ ) ) \left( {r + \gamma \cdot \mathop {\max }\limits_{a'} \hat Q\left( {s,a'} \right)} \right) (r+γ⋅a′maxQ^(s,a′))表示目标 Q Q Q值, Q ( s , a ) Q\left( {s,a} \right) Q(s,a)表示当前的 Q Q Q值。这样,损失函数的目的在于:希望能够尽可能缩小损失值,使得当前基于最新网络权重计算的Q值,能够尽可能接近过去权重估计的目标Q值。打个不确切的比方,相当于利用当前最新的营销手段,来实现过去制订的销售目标。
确立了目标函数后,我们对其进行微分来进行神经网络的训练,其梯度如下所示:
(4) ∇ θ i L i ( θ i ) = ∂ ∂ θ i E s , a ∼ ρ ( ⋅ ) [ ( y i − Q ( s , a ; θ i ) ) 2 ] = ∂ ∂ θ i E s , a ∼ ρ ( ⋅ ) ; s ′ ∼ ε [ ( r + γ ⋅ max a ′ Q ( s ′ , a ′ ; θ i − 1 ) − Q ( s , a ; θ i ) ) 2 ] = E s , a ∼ ρ ( ⋅ ) ; s ′ ∼ ε [ ∂ ∂ θ i ( r + γ ⋅ max a ′ Q ( s ′ , a ′ ; θ i − 1 ) − Q ( s , a ; θ i ) ) 2 ] = E s , a ∼ ρ ( ⋅ ) ; s ′ ∼ ε [ 2 ⋅ ( r + γ ⋅ max a ′ Q ( s ′ , a ′ ; θ i − 1 ) − Q ( s , a ; θ i ) ) ⋅ ∂ ∂ θ i Q ( s , a ; θ i ) ] = E s , a ∼ ρ ( ⋅ ) ; s ′ ∼ ε [ 2 ⋅ ( r + γ ⋅ max a ′ Q ( s ′ , a ′ ; θ i − 1 ) − Q ( s , a ; θ i ) ) ⋅ ∇ θ i Q ( s , a ; θ i ) ] = 2 ⋅ E s , a ∼ ρ ( ⋅ ) ; s ′ ∼ ε [ ( r + γ ⋅ max a ′ Q ( s ′ , a ′ ; θ i − 1 ) − Q ( s , a ; θ i ) ) ⋅ ∇ θ i Q ( s , a ; θ i ) ] \begin{aligned} \nabla_{\theta_i} L_i \left ( \theta_i \right )&= \frac{\partial }{\partial {\theta_i}} \mathbb{E}_{s,a\sim \rho \left ( \cdot \right )}\left [ \left ( y_i - Q\left ( s,a;\theta_i \right ) \right ) ^{2} \right ] \\ &= \frac{\partial }{\partial {\theta_i}} \mathbb{E}_{s,a \sim \rho\left ( \cdot \right );s' \sim \varepsilon } \left [ \left ( r+\gamma \cdot \underset{a'}{\text{max}} Q\left ( s',a';\theta_{i-1} \right ) - Q\left ( s,a;\theta_i \right ) \right )^2 \right ] \\ &= \mathbb{E}_{s,a \sim \rho\left ( \cdot \right );s' \sim \varepsilon } \left [ \frac{\partial }{\partial {\theta_i}} \left ( r+\gamma \cdot \underset{a'}{\text{max}} Q\left ( s',a';\theta_{i-1} \right ) - Q\left ( s,a;\theta_i \right ) \right )^2 \right ] \\ &= \mathbb{E}_{s,a \sim \rho\left ( \cdot \right );s' \sim \varepsilon } \left [ 2 \cdot \left ( r+\gamma \cdot \underset{a'}{\text{max}} Q\left ( s',a';\theta_{i-1} \right ) - Q\left ( s,a;\theta_i \right ) \right ) \cdot \frac{\partial }{\partial {\theta_i}} Q\left ( s,a;\theta_i \right ) \right ] \\ &= \mathbb{E}_{s,a \sim \rho\left ( \cdot \right );s' \sim \varepsilon } \left [ 2 \cdot \left ( r+\gamma \cdot \underset{a'}{\text{max}} Q\left ( s',a';\theta_{i-1} \right )- Q\left ( s,a;\theta_i \right ) \right ) \cdot \nabla_{\theta_i} Q\left ( s,a;\theta_i \right )\right ]\\ &= 2 \cdot \mathbb{E}_{s,a \sim \rho\left ( \cdot \right );s' \sim \varepsilon } \left [ \left ( r+\gamma \cdot \underset{a'}{\text{max}} Q\left ( s',a';\theta_{i-1} \right )- Q\left ( s,a;\theta_i \right ) \right ) \cdot \nabla_{\theta_i} Q\left ( s,a;\theta_i \right )\right ] \end{aligned} \tag {4} ∇θiLi(θi)=∂θi∂Es,a∼ρ(⋅)[(yi−Q(s,a;θi))2]=∂θi∂Es,a∼ρ(⋅);s′∼ε[(r+γ⋅a′maxQ(s′,a′;θi−1)−Q(s,a;θi))2]=Es,a∼ρ(⋅);s′∼ε[∂θi∂(r+γ⋅a′maxQ(s′,a′;θi−1)−Q(s,a;θi))2]=Es,a∼ρ(⋅);s′∼ε[2⋅(r+γ⋅a′maxQ(s′,a′;θi−1)−Q(s,a;θi))⋅∂θi∂Q(s,a;θi)]=Es,a∼ρ(⋅);s′∼ε[2⋅(r+γ⋅a′maxQ(s′,a′;θi−1)−Q(s,a;θi))⋅∇θiQ(s,a;θi)]=2⋅Es,a∼ρ(⋅);s′∼ε[(r+γ⋅a′maxQ(s′,a′;θi−1)−Q(s,a;θi))⋅∇θiQ(s,a;θi)](4)
省略最前面的系数,于是可得:
(5) ∇ θ i L i ( θ i ) = E s , a ∼ ρ ( ⋅ ) ; s ′ ∼ ε [ ( r + γ ⋅ max a ′ Q ( s ′ , a ′ ; θ i − 1 ) − Q ( s , a ; θ i ) ) ⋅ ∇ θ i Q ( s , a ; θ i ) ] \nabla_{\theta_i} L_i \left ( \theta_i \right )=\mathbb{E}_{s,a \sim \rho\left ( \cdot \right );s' \sim \varepsilon } \left [ \left ( r+\gamma \cdot \underset{a'}{\text{max}} Q\left ( s',a';\theta_{i-1} \right )- Q\left ( s,a;\theta_i \right ) \right ) \cdot \nabla_{\theta_i} Q\left ( s,a;\theta_i \right )\right ] \tag {5} ∇θiLi(θi)=Es,a∼ρ(⋅);s′∼ε[(r+γ⋅a′maxQ(s′,a′;θi−1)−Q(s,a;θi))⋅∇θiQ(s,a;θi)](5)
3. 算法描述
DQN的算法描述如下所示,算法出处:Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602. 在线阅读
Initialize replay memory D \mathcal{D} D to capacity N N N
Initialize action-value function Q Q Q with random weights
for episode = 1, M M M do
Initialise sequence s 1 = { x 1 } s_1 = \left\{ x_1 \right\} s1={x1} and pre-processed sequenced ϕ 1 = ϕ ( s 1 ) {\phi _1} = \phi \left( {{s_1}} \right) ϕ1=ϕ(s1)
for t = 1, T T T do
With probability ε \varepsilon ε select a random action at a t a_t at ( ε \varepsilon ε-greedy algorithm)
otherwise select a t = max a Q ∗ ( ϕ ( s t ) , a ; θ ) {a_t} = {\max _a}{Q^*}\left( {\phi \left( {{s_t}} \right),a;\theta } \right) at=maxaQ∗(ϕ(st),a;θ)
Execute action a t a_t at in emulator and observe reward r t r_t rt and image x t + 1 x_{t+1} xt+1
Set s t + 1 = s t , a t , x t + 1 s_{t+1} = s_t, a_t, x_{t+1} st+1=st,at,xt+1 and pre-process ϕ t + 1 = ϕ ( s t + 1 ) \phi_{t+1}=\phi(s_{t+1}) ϕt+1=ϕ(st+1)
Store transition ( ϕ t , a t , r t , ϕ t + 1 ) (\phi_t, a_t, r_t, \phi_{t+1}) (ϕt,at,rt,ϕt+1) in D \mathcal{D} D
Sample random minibatch of transitions ( ϕ j , a j , r j , ϕ j + 1 ) \left ( \phi _{j},a_{j},r_{j},\phi _{j+1} \right ) (ϕj,aj,rj,ϕj+1) from D \mathcal {D} D
Set y i = { r j for terminal ϕ j + 1 r j + γ ⋅ max a ′ Q ( ϕ j + 1 , a ′ ; θ ) for non-terminal ϕ j + 1 y_{i}=\left\{\begin{matrix} r_j\;\;\;\;\text{for terminal}\; \phi_{j+1}\\ r_j+\gamma \cdot \text{max}_{a'}Q\left ( \phi_{j+1},a';\theta \right )\;\;\;\;\text{for non-terminal}\;\;\phi_{j+1} \end{matrix}\right. yi={rjfor terminalϕj+1rj+γ⋅maxa′Q(ϕj+1,a′;θ)for non-terminalϕj+1
Perform a gradient descent step on ( y i − Q ( ϕ j , a j ; θ ) ) 2 \left ( y_i-Q\left ( \phi_j,a_j;\theta \right ) \right )^{2} (yi−Q(ϕj,aj;θ))2 according to Eq. (5) of this blog
end for
end for
上述算法描述中, ϕ \phi ϕ表示 Q Q Q函数。可以发现,这里提供的算法引入了回放记忆(replay memory) 的概念,其作用在于存储过去的学习经历,在网络训练的过程中随机地加入一些学习经历会让训练更加有效。
4. DQN玩CartPole游戏示例
CartPole是gym toolkit中自带的一个小游戏。游戏里面有一个手推车,上有竖着一根杆子,杆子通过一个轴承与手推车相连。当手推车运动起来时,由于惯性,杆子有倒下来的趋势,因此小车需要左右移动来保持杆子竖直。如果杆子倾斜的角度大于15°,那么游戏结束。小车也不能移动出一个范围(中间到两边各2.4个单位长度)。手推车一旦开始运动就开始计时,在游戏结束之前,坚持的时间越长,得分越高。游戏原理如下图所示:
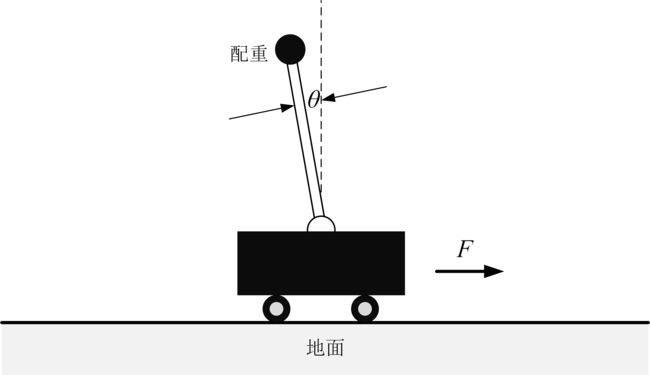
如果想手动玩这个游戏亲自体验一下,可以访问这个网站:https://fluxml.ai/experiments/cartPole/ ,玩的时候按左、右方向键即可。
下面简要分析一下DQN玩CartPole游戏的代码。源码下载:https://github.com/ljpzzz/machinelearning/blob/master/reinforcement-learning/dqn.py
4.1 游戏接口定义
CartPole游戏的State定义为:
- Cart Position(位置)
- Cart Velocity(速度)
- Pole Angle(杆子的夹角)
- Pole Velocity At Tip(杆子顶端小部件的速度)
Action定义为:
- Push left
- Push right
Reward定义为:
- 每经历一个时间步长step,reward +1
4.2 网络结构
首先看一下网络结构设计,代码使用了一个简单的多层感知机(Multi-layer perceptron,MLP),包含一个输入层(State),一个隐藏层和一个输出层( Q Q Q value),共三层,层与层之间的节点进行全连接,如下图所示:
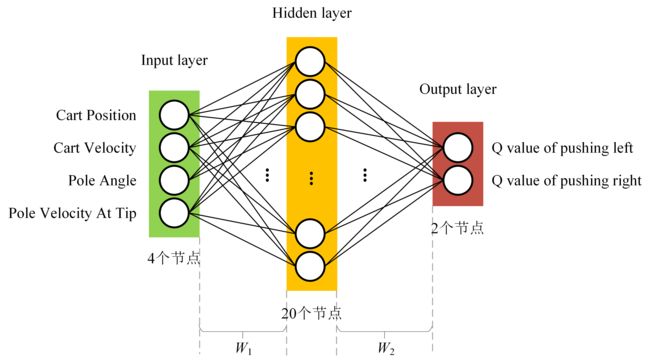
深度神经网络创建函数的完整代码如下所示:
def create_Q_network(self):
# network weights
W1 = self.weight_variable([self.state_dim,20])
b1 = self.bias_variable([20])
W2 = self.weight_variable([20,self.action_dim])
b2 = self.bias_variable([self.action_dim])
# input layer
self.state_input = tf.placeholder("float",[None,self.state_dim])
# hidden layers
h_layer = tf.nn.relu(tf.matmul(self.state_input,W1) + b1)
# Q Value layer
self.Q_value = tf.matmul(h_layer,W2) + b2
其中W1对应State,它的shape为[4, 20],即4行,20列。W2对应Action,它的shape为[2, 20]。结合上面的示意图可以看出,W1的4行对应输入State的4种状态,W2的2行对应输出的两种动作。
4.3 网络训练
源码采用Adam优化算法进行网络参数训练,训练阶段主要包括两个步骤:
-
从回放记忆中随机地抽取一些数据(相当于历史经验),读入到变量minibatch中。minibatch中每一个元素,其内部包含五个字段:state、action、reward、next_state和一个“done”标志位(这里的done标志位由gym游戏环境进行裁判并赋值,它表示在玩游戏的过程中,当前的状态是否可以结束)。结束条件为:
① Pole Angle is more than ±12°
② Cart Position is more than ±2.4 (center of the cart reaches the edge of the display)
③ Episode length is greater than 200 -
计算目标 Q Q Q值(target Q Q Q),如公式(2)所示:
(2) y i = E s ′ ∼ ε [ r + γ ⋅ max a ′ Q ( s ′ , a ′ ; θ i − 1 ) ∣ s , a ] y_i=\mathbb{E}_{s' \sim \varepsilon }\left [ r+\gamma \cdot \text{max}_{a'} Q\left ( s',a';\theta_{i-1} \right ) \mid s,a \right ] \tag {2} yi=Es′∼ε[r+γ⋅maxa′Q(s′,a′;θi−1)∣s,a](2)
示例源码用变量y_batch来表示目标 Q Q Q值,用语句reward_batch[i] + GAMMA * np.max(Q_value_batch[i])进行计算。在计算过程中,需要依赖对 max a ′ Q ( s ′ , a ′ ; θ i − 1 ) \text{max}_{a'} Q\left ( s',a';\theta_{i-1} \right ) maxa′Q(s′,a′;θi−1)的计算,这里源码采用的是神经网络传导的方式来计算目标 Q Q Q值(这也正是DQN方法与传统Q-learning方法的不同之处),如下所示:
Q_value_batch = self.Q_value.eval(feed_dict={self.state_input:next_state_batch})
网络训练函数的完整代码如下所示:
def create_training_method(self):
self.action_input = tf.placeholder("float",[None,self.action_dim]) # one hot presentation
self.y_input = tf.placeholder("float",[None])
Q_action = tf.reduce_sum(tf.multiply(self.Q_value,self.action_input),reduction_indices = 1)
self.cost = tf.reduce_mean(tf.square(self.y_input - Q_action))
self.optimizer = tf.train.AdamOptimizer(0.0001).minimize(self.cost)
def train_Q_network(self):
self.time_step += 1
# Step 1: obtain random minibatch from replay memory
minibatch = random.sample(list(self.replay_buffer), BATCH_SIZE)
state_batch = [data[0] for data in minibatch]
action_batch = [data[1] for data in minibatch]
reward_batch = [data[2] for data in minibatch]
next_state_batch = [data[3] for data in minibatch]
# Step 2: calculate y
y_batch = []
Q_value_batch = self.Q_value.eval(feed_dict={self.state_input:next_state_batch})
for i in range(0,BATCH_SIZE):
done = minibatch[i][4]
if done:
y_batch.append(reward_batch[i])
else :
y_batch.append(reward_batch[i] + GAMMA * np.max(Q_value_batch[i]))
self.optimizer.run(feed_dict={
self.y_input:y_batch,
self.action_input:action_batch,
self.state_input:state_batch
})
4.4 动作选择( ε \varepsilon ε-greedy算法)
Agent在玩游戏时,会利用贪心算法进行动作探索。Agent在选择动作时,会随机地探索动作,或者直接根据 Q Q Q值来选择动作,其完整代码如下所示:
def egreedy_action(self,state):
Q_value = self.Q_value.eval(feed_dict = {
self.state_input:[state]
})[0]
if random.random() <= self.epsilon:
self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / 10000
return random.randint(0,self.action_dim - 1)
else:
self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / 10000
return np.argmax(Q_value)
4.5 main函数
在每一个episode中,分为两个阶段:training和testing(testing仅限100整数倍数的episode)。其完整代码如下所示:
def main():
# initialize OpenAI Gym env and dqn agent
env = gym.make(ENV_NAME)
agent = DQN(env)
for episode in range(EPISODE):
# initialize task
state = env.reset()
# Train
for step in range(STEP):
action = agent.egreedy_action(state) # e-greedy action for train
next_state,reward,done,_ = env.step(action)
# Define reward for agent
reward = -1 if done else 0.1
agent.perceive(state,action,reward,next_state,done)
state = next_state
if done:
break
# Test every 100 episodes
if episode % 100 == 0:
total_reward = 0
for i in range(TEST):
state = env.reset()
for j in range(STEP):
env.render()
action = agent.action(state) # direct action for test
state,reward,done,_ = env.step(action)
total_reward += reward
if done:
break
ave_reward = total_reward/TEST
print ('episode: ',episode,'Evaluation Average Reward:',ave_reward)
4.6 Putting It All Together(from Pinard)
完整源码如下所示(单文件Python源码):
#######################################################################
# Copyright (C) #
# 2016 - 2019 Pinard Liu([email protected]) #
# https://www.cnblogs.com/pinard #
# Permission given to modify the code as long as you keep this #
# declaration at the top #
#######################################################################
##https://www.cnblogs.com/pinard/p/9714655.html ##
## 强化学习(八)价值函数的近似表示与Deep Q-Learning ##
import gym
import tensorflow as tf
import numpy as np
import random
from collections import deque
# Hyper Parameters for DQN
GAMMA = 0.9 # discount factor for target Q
INITIAL_EPSILON = 0.5 # starting value of epsilon
FINAL_EPSILON = 0.01 # final value of epsilon
REPLAY_SIZE = 10000 # experience replay buffer size
BATCH_SIZE = 32 # size of minibatch
class DQN():
# DQN Agent
def __init__(self, env):
# init experience replay
self.replay_buffer = deque()
# init some parameters
self.time_step = 0
self.epsilon = INITIAL_EPSILON
self.state_dim = env.observation_space.shape[0]
self.action_dim = env.action_space.n
self.create_Q_network()
self.create_training_method()
# Init session
self.session = tf.InteractiveSession()
self.session.run(tf.global_variables_initializer())
def create_Q_network(self):
# network weights
W1 = self.weight_variable([self.state_dim,20])
b1 = self.bias_variable([20])
W2 = self.weight_variable([20,self.action_dim])
b2 = self.bias_variable([self.action_dim])
# input layer
self.state_input = tf.placeholder("float",[None,self.state_dim])
# hidden layers
h_layer = tf.nn.relu(tf.matmul(self.state_input,W1) + b1)
# Q Value layer
self.Q_value = tf.matmul(h_layer,W2) + b2
def create_training_method(self):
self.action_input = tf.placeholder("float",[None,self.action_dim]) # one hot presentation
self.y_input = tf.placeholder("float",[None])
Q_action = tf.reduce_sum(tf.multiply(self.Q_value,self.action_input),reduction_indices = 1)
self.cost = tf.reduce_mean(tf.square(self.y_input - Q_action))
self.optimizer = tf.train.AdamOptimizer(0.0001).minimize(self.cost)
def perceive(self,state,action,reward,next_state,done):
one_hot_action = np.zeros(self.action_dim)
one_hot_action[action] = 1
self.replay_buffer.append((state,one_hot_action,reward,next_state,done))
if len(self.replay_buffer) > REPLAY_SIZE:
self.replay_buffer.popleft()
if len(self.replay_buffer) > BATCH_SIZE:
self.train_Q_network()
def train_Q_network(self):
self.time_step += 1
# Step 1: obtain random minibatch from replay memory
minibatch = random.sample(list(self.replay_buffer), BATCH_SIZE)
state_batch = [data[0] for data in minibatch]
action_batch = [data[1] for data in minibatch]
reward_batch = [data[2] for data in minibatch]
next_state_batch = [data[3] for data in minibatch]
# Step 2: calculate y
y_batch = []
Q_value_batch = self.Q_value.eval(feed_dict={self.state_input:next_state_batch})
for i in range(0,BATCH_SIZE):
done = minibatch[i][4]
if done:
y_batch.append(reward_batch[i])
else :
y_batch.append(reward_batch[i] + GAMMA * np.max(Q_value_batch[i]))
self.optimizer.run(feed_dict={
self.y_input:y_batch,
self.action_input:action_batch,
self.state_input:state_batch
})
def egreedy_action(self,state):
Q_value = self.Q_value.eval(feed_dict = {
self.state_input:[state]
})[0]
if random.random() <= self.epsilon:
self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / 10000
return random.randint(0,self.action_dim - 1)
else:
self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / 10000
return np.argmax(Q_value)
def action(self,state):
return np.argmax(self.Q_value.eval(feed_dict = {
self.state_input:[state]
})[0])
def weight_variable(self,shape):
initial = tf.truncated_normal(shape)
return tf.Variable(initial)
def bias_variable(self,shape):
initial = tf.constant(0.01, shape = shape)
return tf.Variable(initial)
# ---------------------------------------------------------
# Hyper Parameters
ENV_NAME = 'CartPole-v0'
EPISODE = 3000 # Episode limitation
STEP = 300 # Step limitation in an episode
TEST = 10 # The number of experiment test every 100 episode
def main():
# initialize OpenAI Gym env and dqn agent
env = gym.make(ENV_NAME)
agent = DQN(env)
for episode in range(EPISODE):
# initialize task
state = env.reset()
# Train
for step in range(STEP):
action = agent.egreedy_action(state) # e-greedy action for train
next_state,reward,done,_ = env.step(action)
# Define reward for agent
reward = -1 if done else 0.1
agent.perceive(state,action,reward,next_state,done)
state = next_state
if done:
break
# Test every 100 episodes
if episode % 100 == 0:
total_reward = 0
for i in range(TEST):
state = env.reset()
for j in range(STEP):
env.render()
action = agent.action(state) # direct action for test
state,reward,done,_ = env.step(action)
total_reward += reward
if done:
break
ave_reward = total_reward/TEST
print ('episode: ',episode,'Evaluation Average Reward:',ave_reward)
if __name__ == '__main__':
main()
运行效果如下面的动图所示:
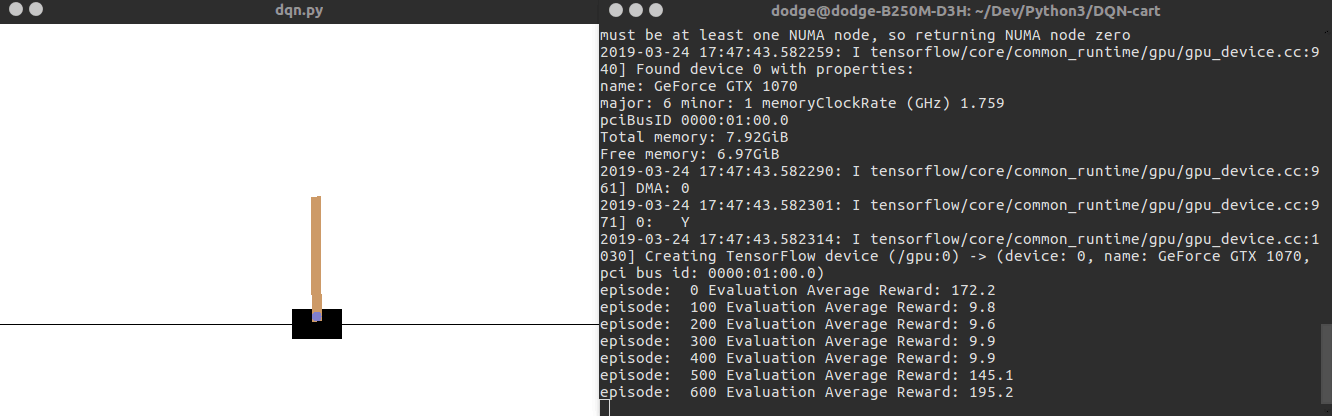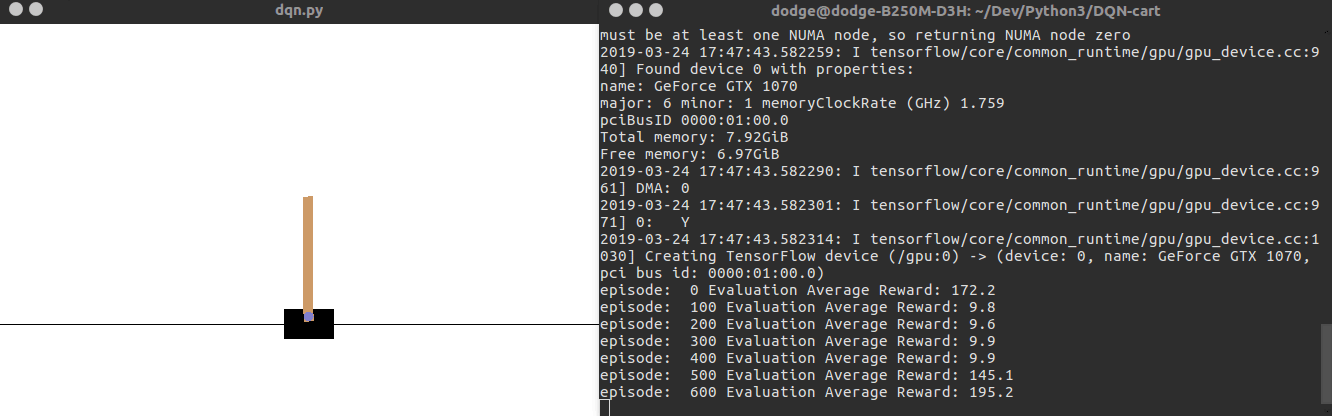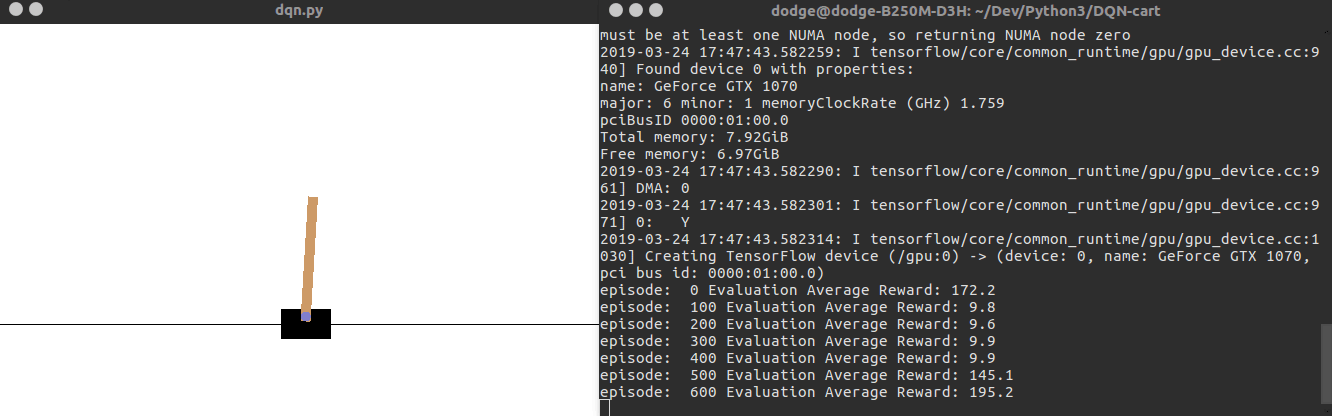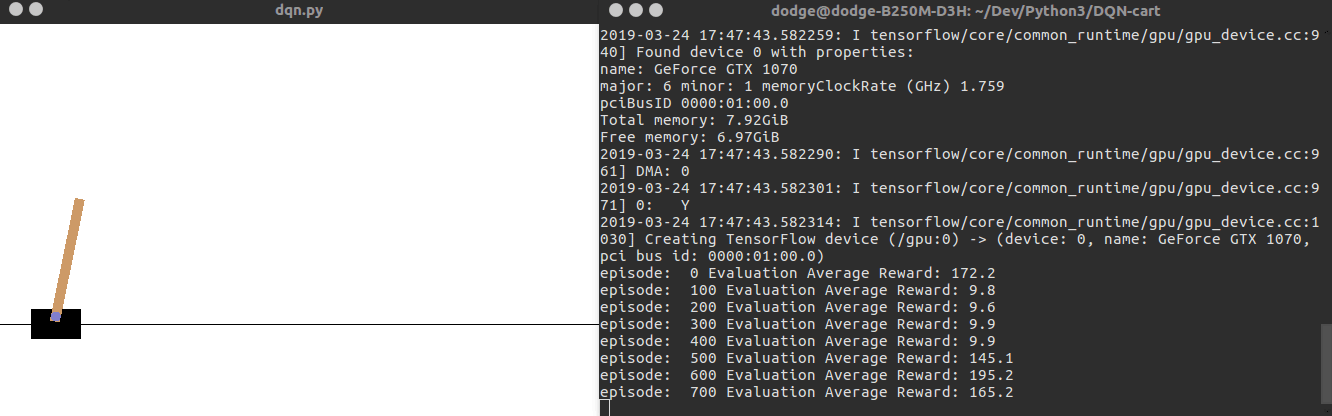
源码运行笔记请参考:https://blog.csdn.net/discoverer100/article/details/88770046
5. 小结
本笔记简要说明了Deep Q-Network(DQN)的基本原理,并结合一个具体示例说明了如何构建一个DQN来实现深度强化学习算法。可以看出,DQN的最大特色在于,将传统Q-learning中的 Q Q Q值计算部分替换成了利用网络的正向传播进行,这也是Q-learning方法与深度学习方法结合最显著的地方。
最后,非常感谢Pinard同学的无私分享,他的博客中有许多文章对深度强化学习进行了深入研究,推荐阅读:https://www.cnblogs.com/pinard/
参考资料:
- Reinforcement learning – Part 2: Getting started with Deep Q-Networks
- 强化学习笔记(2)-从 Q-Learning 到 DQN
- Deep Q-Learning with Keras and Gym
- Playing Atari with Deep Reinforcement Learning
- AI学习笔记——深度Q-Learning(Deep Q-Learing(DQN))
- 强化学习(八)价值函数的近似表示与Deep Q-Learning
- CartPole-v0