起步
决策树(decision tree)是一个树结构,可以是二叉树或非二叉树,也可以把他看作是 if-else 规则的集合,也可以认为是在特征空间上的条件概率分布。
决策树的结构
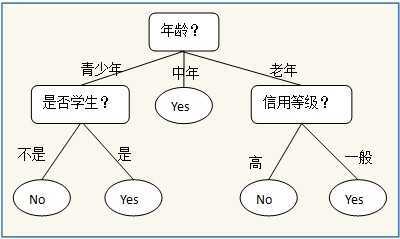
以一个简单的用于是否买电脑预测的决策树为例子:
树中的内部节点代表一个属性,节点引出的分支表示这个属性的所有可能的值,叶节点表示最终的分类结果。从根节点到叶节点的每一条路径构建一条规则,并且这些规则具有 互斥且完备 的性质,即每一个样本均被且只有一条路径所覆盖。
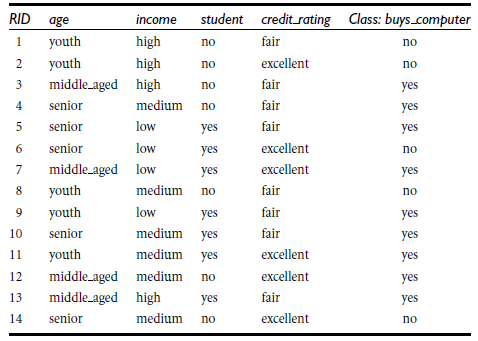
决策树的创建是根据给定的训练数据来完成的,给出下面的训练集(本章都是围着这个例子进行讲解):
这是一个是否买电脑的一个数据,数据上有4个特征:年龄( age ),收入( income ),是否学生( student ),信用度( credit_rating )。
案例的决策树中,为什么是以年龄作为第一个进行分类的特征呢?
特征的分类能力
如果一个特征对结果影响比较大,那么就可以认为这个特征的分类能力比较大。相亲时候一般会先问收入,再问长相,然后问其家庭情况。也就是说在这边收入情况影响比较大,所以作为第一个特征判断,如果不合格那可能连后续都不用询问了。
有什么方法可以表明特征的分类能力呢?
这时候,需要引入一个概念,熵 。
熵(entropy)
1948年,香农提出“信息熵”的概率。一条信息的信息量大小和它的不确定性有直接的关系,要搞清楚一件不确定的事,需要了解大量信息。熵(entropy)用于表示 随机变量不确定性的度量, 如果熵越大,表示不确定性越大。
假设变量X,它有Xi(i=1,2,3...n)种情况,pi表示第i情况的概率,那么随机变量X的熵定义为:
$$ H(X) = -\sum_{i=1}^np_i\log_2{(p_i)} $$
熵的单位是比特(bit)。
比如当随机变量X只有0,1两种取值,则有: H(x) = -plog(p) - (1-p)log(1-p) , 可以画出一个二维坐标表示他们的关系:
从而可知,当 p=0.5 时,熵取值最大,随机变量不确定性最大。
回到买电脑的例子,在是否购买电脑这个结果中,数据集D,有 9 个yes,5 个no。因此它的熵是:
$$ info(D) = H(D) = - \frac{9}{14}\log_2(\frac{9}{14}) - \frac5{14}\log_2(\frac5{14}) = 0.940 bits $$
条件熵(conditional entropy)
随机变量X给定的条件下,随机变量Y的条件熵 H(Y|X) 定义为:
$$ H(Y|X) = \sum_{i=1}^np_iH(Y|X=x_i) $$
信息增益 (Information gain)
信息增益表示的是:得知 特征X 的信息而使得 分类Y 的信息的不确定性减少的程度。如果某个特征的信息增益比较大,就表示该特征对结果的影响较大,特征A对数据集D的信息增益表示为:
$$ gain(A) = H(D) - H(D|A) $$
以那个买电脑的数据集为例,我们来计算下 age 这个特征的信息增益,将数据再展示一下:
从图中可以看出,有14条数据 age 这个特征中,年轻人 youth 有5人, 中年人 middle_aged 有4人,老年人 senior 有5人。分别计算这三种情况下的信息熵,再将信息熵相加就能得到 H(D|A):
$$ \begin{align*} info_{age}(D) = H(D|A) &= \frac5{14}\times (-\frac25\log_2\frac25 - \frac35\log_2\frac35) \\ &+\frac4{14}\times (-\frac44\log_2\frac44 - \frac04\log_2\frac04) \\ &+\frac5{14}\times (-\frac35\log_2\frac35 - \frac25\log_2\frac25) \\ &=0.694 bits \end{align*} $$
因此,gain(age) 的信息增益就是:
gain(age) = info(D) - info_{age}(D) = 0.940 - 0.694 = 0.246 bits决策树归纳算法 (ID3)
ID3算法的核心是在决策树的各个结点上应用 信息增益 准则进行特征选择。这个算法也是本章主要介绍的算法。具体做法是:
- 从根节点开始,对结点计算所有可能特征的信息增益,选择信息增益最大的特征作为结点的特征,并由该特征的不同取值构建子节点;
- 对子节点递归地调用以上方法,构建决策树;
- 直到所有特征的信息增益均很小或者没有特征可选时为止。
根据上面的计算信息增量的方法,可以得出其他特征的信息增量:gain(income) = 0.029, gain(student) = 0.151, gain(credit_rating)=0.048 。
age 这个特征的信息增益是最大的(0.246 bits),选择age作为第一个根节点进行分类:
然后再每个子树中,再根据其特征的信息增益量进行每个划分,递归地形成每个划分上的样本判定树。
递归的停止条件
递归划分步骤仅当下列条件之一成立停止:
(a) 给定结点的所有样本属于同一类。
(b) 没有剩余属性可以用来进一步划分样本。在此情况下,使用多数表决。这涉及将给定的结点转换成树叶,并用样本中的多数所在的类标记它。替换地,可以存放结点样本的类分布。
(c) 分枝,当所有特征的信息增益都很小,也就是没有再计算的必要了,就创建一个树叶,也是用多数表决。
其他决策树归纳算法
C4.5算法
C4.5算法与ID3算法的区别主要在于它在生产决策树的过程中,使用信息增益比来进行特征选择。
CART算法
分类与回归树(classification and regression tree,CART)与C4.5算法一样,由ID3算法演化而来。CART假设决策树是一个二叉树,它通过递归地二分每个特征,将特征空间划分为有限个单元,并在这些单元上确定预测的概率分布。
CART算法中,对于回归树,采用的是平方误差最小化准则;对于分类树,采用基尼指数最小化准则。
这些算法共同点:都是贪心算法,自上而下的创建决策树。不同点是在于对特征的选择度量方法不同。
决策树的剪枝
如果树长到叶子深度太大,就会造成一种情况,在训练集上表现非常好,但是因为分的太细了,在新的数据上就表现不好了。就是出现过度拟合的现象。为了避免这个问题,有两种解决办法:
- 先剪枝:当熵减少的数量小于某一个阈值时,就停止分支的创建。这是一种贪心算法。
- 后剪枝:先创建完整的决策树,然后再尝试消除多余的节点,也就是采用减枝的方法。
总结:决策树的优缺点
优点:
- 易于理解和解释,甚至比线性回归更直观;
- 与人类做决策思考的思维习惯契合;
- 模型可以通过树的形式进行可视化展示;
- 可以直接处理非数值型数据,不需要进行哑变量的转化,甚至可以直接处理含缺失值的数据;
缺点:
- 处理连续变量不好;
- 不好处理变量之间存在许多错综复杂的关系,如金融数据分析;
- 决定分类的因素取决于更多变量的复杂组合时;
- 可规模性一般。