一.学习总结
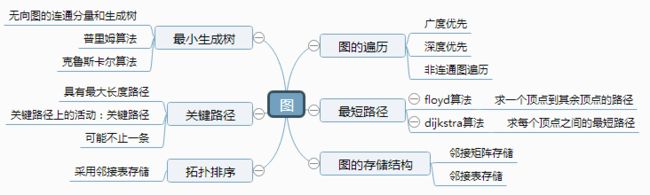
1.图的思维导图
2.图结构学习体会
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径, 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。拓扑排序是对有向无圈图的顶点的一种排序,使得如果存在一条从Vi到Vj的路径,那么排序中Vj一定出现在Vi后面,所以图里面有圈就不能完成排序。图的遍历中,可用邻接表实现广度优先遍历,用邻接矩阵实现深度优先遍历。Prim算法: Prim算法实现的是找出一个有权重连通图中的最小生成树,即:具有最小权重且连接到所有结点的树。(强调的是树,树是没有回路的)。Kruskal算法与Prim算法的不同之处在于,Kruskal在找最小生成树结点之前,需要对所有权重边做从小到大排序。将排序好的权重边依次加入到最小生成树中,如果加入时产生回路就跳过这条边,加入下一条边。当所有结点都加入到最小生成树中之后,就找出了最小生成树
二.PTA实验作业
题目一.:排座位
设计思路
int Find(int x) //用于查找根节点
int a=Find(i1);int b=Find(i2)
if(a==b&&ma[i1][i2]!=-1)
else if(a!=b&&ma[i1][i2]==-1)
else if(a==b&&ma[i1][i2]==-1) //判断是否有共同的朋友,即根结点是否相同;是否敌对
代码截图
PTA提交列表说明
题目二:公路村村通
设计思路
iint prime() //用prime算法求出最小权值之和,即最小费用
代码截图
PTA提交列表说明
题目三:图着色问题
设计思路
代码截图
PTA提交列表说明
三.PTA排名
我的分数:190分
四.阅读代码
void dijkstra(Graph G, int vs, int prev[], int dist[]) {
int i,j,k;
int min;
int tmp;
int flag[MAX]; // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。 // 初始化
for (i = 0; i < G.vexnum; i++) {
flag[i] = 0; // 顶点i的最短路径还没获取到。
prev[i] = 0; // 顶点i的前驱顶点为0。
dist[i] = G.matrix[vs][i];// 顶点i的最短路径为"顶点vs"到"顶点i"的权。
} // 对"顶点vs"自身进行初始化
flag[vs] = 1;
dist[vs] = 0; // 遍历G.vexnum-1次;每次找出一个顶点的最短路径。
for (i = 1; i < G.vexnum; i++) {
// 寻找当前最小的路径;
// 即,在未获取最短路径的顶点中,找到离vs最近的顶点(k)。
min = INF;
for (j = 0; j < G.vexnum; j++) {
if (flag[j]==0 && dist[j] min = dist[j]; k = j; } } // 标记"顶点k"为已经获取到最短路径 flag[k] = 1; // 修正当前最短路径和前驱顶点 // 即,当已经"顶点k的最短路径"之后,更新"未获取最短路径的顶点的最短路径和前驱顶点"。 for (j = 0; j < G.vexnum; j++) { tmp = (G.matrix[k][j]==INF ? INF : (min + G.matrix[k][j])); // 防止溢出 if (flag[j] == 0 && (tmp < dist[j]) ) { dist[j] = tmp; prev[j] = k; } } } // 打印dijkstra最短路径的结果 printf("dijkstra(%c): \n", G.vexs[vs]); for (i = 0; i < G.vexnum; i++) printf(" shortest(%c, %c)=%d\n", G.vexs[vs], G.vexs[i], dist[i]); } 这一个代码是用Dijstra算法求最短路径