LeetCode 刷题记录 40. Combination Sum II
题目:
Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sums to target.
Each number in candidates may only be used once in the combination.
Note:
All numbers (including target) will be positive integers.
The solution set must not contain duplicate combinations.
Example 1:
Input: candidates = [10,1,2,7,6,1,5], target = 8,
A solution set is:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
Example 2:
Input: candidates = [2,5,2,1,2], target = 5,
A solution set is:
[
[1,2,2],
[5]
]
本题与LeetCode 刷题记录 39. Combination Sum很类似
两点不同:
- Combination Sum中candidates中没有重复的元素,而Combination Sum II中元素可以重复,并且结果集中不能有重复
- 每个元素只能用一次,而不是像Combination Sum中元素可以重复使用
第二点很好处理,在递归函数中每次调用i+1而不是i
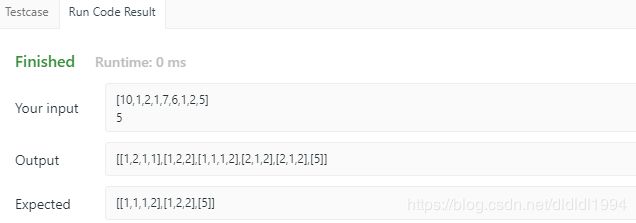
首先我们先用Combination Sum解法1,仅将i变为i+1
class Solution {
public:
vector> combinationSum2(vector& candidates, int target) {
vector> res;
vector path;
DFS(candidates, path, res, target, 0);
return res;
}
void DFS(vector& candidates, vector& path,vector>& res,int gap,int start){
if(gap < 0) return;
if(gap == 0){
res.push_back(path);
return;
}
for(int i = start; i < candidates.size(); ++i){
path.push_back(candidates[i]);
DFS(candidates, path, res, gap - candidates[i], i + 1);
path.pop_back();
}
}
};
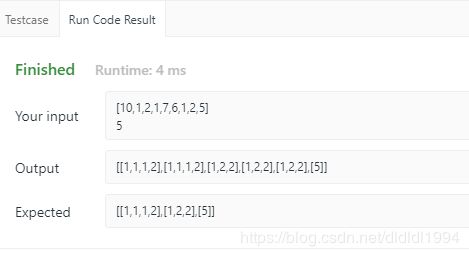
所以必须要将数组先进行排序处理
class Solution {
public:
vector> combinationSum2(vector& candidates, int target) {
vector> res;
vector path;
sort(candidates.begin(), candidates.end());
DFS(candidates, path, res, target, 0);
return res;
}
void DFS(vector& candidates, vector& path,vector>& res,int gap,int start){
if(gap < 0) return;
if(gap == 0){
res.push_back(path);
return;
}
for(int i = start; i < candidates.size(); ++i){
//if(i > start && candidates[i] == candidates[i-1]) continue;
path.push_back(candidates[i]);
DFS(candidates, path, res, gap - candidates[i], i + 1);
path.pop_back();
}
}
};
if(i > start && candidates[i] == candidates[i-1]) continue;
才能实现去重操作
解法1:
递归法:不剪枝
设 candidates数组[1,2,1,1,2,5] target = 5
排序数组[1,1,1,2,2,5]
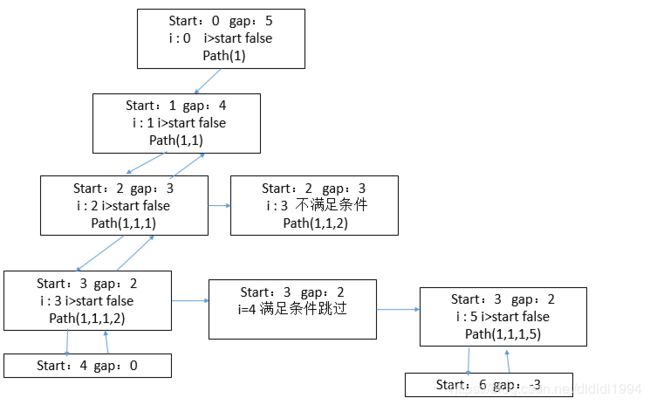
我们用cout语句打印出满足去重条件的start i 和i - 1值

i=start 说明start所处的元素第一次加入path不用判断重复
i>start 说明start所处的元素已经出path,这时候可以判断重复
如:start 3 i 4 i-1 3 ,start为3的元素1已经出path, i = 4 值为2,与i = 3值相等,说明我们已经加过 i = 3的2,无需加i = 4的2
c++:
class Solution {
public:
vector> combinationSum2(vector& candidates, int target) {
vector> res;
vector path;
sort(candidates.begin(), candidates.end());
DFS(candidates, path, res, target, 0);
return res;
}
void DFS(vector& candidates, vector& path,vector>& res,int gap,int start){
if(gap < 0) return;
if(gap == 0){
res.push_back(path);
return;
}
for(int i = start; i < candidates.size(); ++i){
if(i > start && candidates[i] == candidates[i-1]) continue;
path.push_back(candidates[i]);
DFS(candidates, path, res, gap - candidates[i], i + 1);
path.pop_back();
}
}
};
java:
class Solution {
public List> combinationSum2(int[] candidates, int target) {
List> res = new ArrayList<>();
List path = new ArrayList<>();
Arrays.sort(candidates);
//DFS(candidates, new ArrayList<>(), res, target, 0);
DFS(candidates, path, res, target, 0);
return res;
}
private void DFS(int[] candidates,List path,List> res,int gap,int start){
if(gap < 0) return;
if(gap == 0){
res.add(new ArrayList<>(path));
return;
}
for(int i = start; i < candidates.length; ++i){
// cout << candidates[i] << endl;
// if(gap < candidates[i]) return;
if(i > start && candidates[i] == candidates[i-1]) continue;
path.add(candidates[i]);
DFS(candidates, path, res, gap - candidates[i], i + 1);
path.remove(path.size() - 1);
}
}
}
python:
class Solution(object):
def combinationSum2(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
res = []
candidates.sort()
self.DFS(candidates, [], res, target, 0)
return res
def DFS(self, candidates, path, res,gap,start):
if gap < 0: return
if gap == 0:
res.append(path)
return
for i in xrange(start, len(candidates)):
if i > start and candidates[i] == candidates[i-1]: continue;
#if gap < candidates[i]: return
#path.append(candidates[i])
self.DFS(candidates, path + [candidates[i]], res, gap - candidates[i], i + 1)
#self.DFS(candidates, path, res, gap - candidates[i], i)
#path.pop()
解法2:
递归法 剪枝
c++:
class Solution {
public:
vector> combinationSum2(vector& candidates, int target) {
vector> res;
vector path;
sort(candidates.begin(), candidates.end());
DFS(candidates, path, res, target, 0);
return res;
}
void DFS(vector& candidates, vector& path,vector>& res,int gap,int start){
// if(gap < 0) return;
if(gap == 0){
res.push_back(path);
return;
}
for(int i = start; i < candidates.size(); ++i){
if(i > start && candidates[i] == candidates[i-1]) continue;
if(gap < candidates[i]) return;
path.push_back(candidates[i]);
DFS(candidates, path, res, gap - candidates[i], i + 1);
path.pop_back();
}
}
};
java:
class Solution {
public List> combinationSum2(int[] candidates, int target) {
List> res = new ArrayList<>();
List path = new ArrayList<>();
Arrays.sort(candidates);
DFS(candidates, path, res, target, 0);
return res;
}
private void DFS(int[] candidates,List path,List> res,int gap,int start){
//if(gap < 0) return;
if(gap == 0){
res.add(new ArrayList<>(path));
return;
}
for(int i = start; i < candidates.length; ++i){
// cout << candidates[i] << endl;
if(i > start && candidates[i] == candidates[i-1]) continue;
if(gap < candidates[i]) return;
path.add(candidates[i]);
DFS(candidates, path, res, gap - candidates[i], i + 1);
path.remove(path.size() - 1);
}
}
}
python:
class Solution(object):
def combinationSum2(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
res = []
candidates.sort()
self.DFS(candidates, [], res, target, 0)
return res
def DFS(self, candidates, path, res,gap,start):
#if gap < 0: return
if gap == 0:
res.append(path)
return
for i in xrange(start, len(candidates)):
if i > start and candidates[i] == candidates[i-1]: continue;
if gap < candidates[i]: return
#path.append(candidates[i])
self.DFS(candidates, path + [candidates[i]], res, gap - candidates[i], i + 1)
#self.DFS(candidates, path, res, gap - candidates[i], i)
#path.pop()