---恢复内容开始---
1.学习总结(2分)
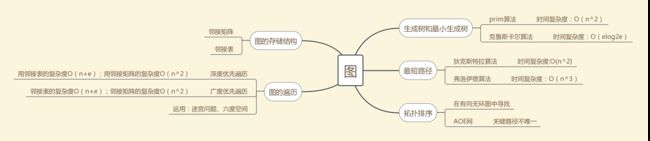
1.1图的思维导图
1.2 图结构学习体会
深度遍历算法:当节点v的所有边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
广度遍历算法:也叫宽度遍历算法,是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。
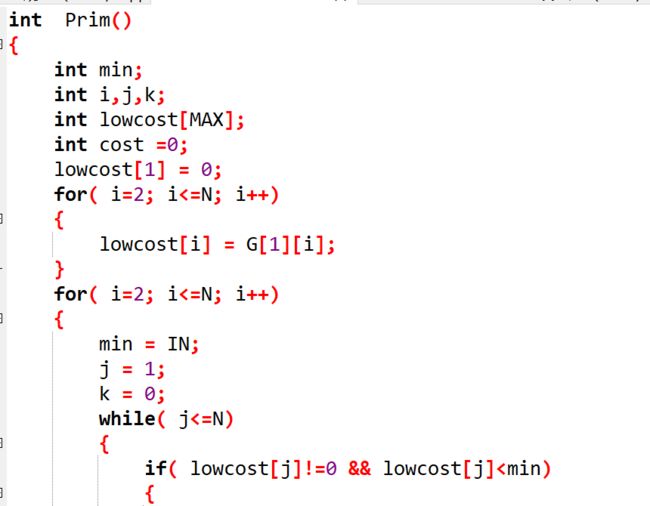
Prim和Kruscal算法:Prim算法是先将找到顶点,再找到该顶点与相邻顶点间权值最小的那一条,以此类推;Kruscal算法是先找到该图中权值最小的那条边,将他记录下来,再去找第二小的,如无产生回路就将其记录下来,以此类推
Dijkstra算法:还是利用数组来找出最短路径,先循环遍历出第一个顶点A离其他顶点的距离,然后存储到一个数组里,这时候数组里对应的每一位就是各个顶点到A的距离。
找出距离最小的那个顶点B,重新计算B到其他顶点的距离,这里有一点要说明一下:比如顶点C,他到顶点A的路径可能经过B,又或者直接从A到C。这时候就需要A到B的距离加上B到C的距离之和与A到C的距离做比较,取出较小的那个存储到数组中。
拓扑排序算法:是一个有向无环图的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
2.PTA实验作业(4分)
本周要求挑选出3道题目书写设计思路、调试过程。设计思路使用伪代码描述。题目选做要求:
题目1:7-1 图着色问题(25 分)
2.2 设计思路(伪代码或流程图)
int main() { 输入无向图的顶点数、边数、以及颜色数 从i=1到e循环{ 输入一条边的两个端点的编号 并将其关系赋值为1; } 创建一个邻接矩阵 将待测方案输入后在矩阵中判断时候满足条件 如果不满足,输出no; 否则输出yes; return 0; }
2.3 代码截图
2.4 PTA提交列表说明
一开始编译错误是因为在将代码从外环境放到PTA上时出错,少了大括号
在判断条件时,没有考虑有颜色数超过K、颜色编号不是从1开始、相邻点同色以及图不连通的错误,之后修改了条件后运行通过
题目2:7-3 六度空间(30 分)
2.2 设计思路(伪代码或流程图)
int main() { 定义 整型变量i, a, b, j,浮点型t; 输入n,m 给head初始化 循环输入结点关系 从i=1到i=n循环 { vis初始化 t = bfs(i) * 100.0 / n; 输出结点及其所占百分比 } return 0; }
2.3 代码截图
2.4 PTA提交列表说明。
一开始的时候,有些变量没有定义为全局变量,导致了编译错误;
在写循环条件的时候,没有考虑无向图的条件,之后将循环条件改成i = head[u.cen] ; i != -1 ; i = e[i].next之后就可以通过了
题目2:7-4 公路村村通(30 分)
2.2 设计思路(伪代码或流程图)
int main() { 定义flag并赋初值 输入N和M; 根据题目所给的顶点及权值创建图 本题选用Prim算法来解,返回值为最小成本,赋给flag 输出flag; return 0; }
2.3 代码截图
2.4 PTA提交列表说明
一开始写的时候没有注意到编译环境没有改,一直答案错误,之后改过来了;
后来编译的时候发现自没有注意到M 本次题目集总分:310分 大家倒垃圾的时候,都希望垃圾箱距离自己比较近,但是谁都不愿意守着垃圾箱住。所以垃圾箱的位置必须选在到所有居民点的最短距离最长的地方,同时还要保证每个居民点都在距离它一个不太远的范围内。 现给定一个居民区的地图,以及若干垃圾箱的候选地点,请你推荐最合适的地点。如果解不唯一,则输出到所有居民点的平均距离最短的那个解。如果这样的解还是不唯一,则输出编号最小的地点。 输入格式: 输入第一行给出4个正整数:N(<= 103)是居民点的个数;M(<= 10)是垃圾箱候选地点的个数;K(<= 104)是居民点和垃圾箱候选地点之间的道路的条数;DS是居民点与垃圾箱之间不能超过的最大距离。所有的居民点从1到N编号,所有的垃圾箱候选地点从G1到GM编号。 随后K行,每行按下列格式描述一条道路: 输出格式: 首先在第一行输出最佳候选地点的编号。然后在第二行输出该地点到所有居民点的最小距离和平均距离。数字间以空格分隔,保留小数点后1位。如果解不存在,则输出“No Solution”。 代码如下: 3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名(截图带自己名字的排名)
3.2 我的总分:

4. 阅读代码(必做,1分)
垃圾箱分布
P1 P2 Dist
其中P1和P2是道路两端点的编号,端点可以是居民点,也可以是垃圾箱候选点。Dist是道路的长度,是一个正整数。4 3 11 5
1 2 2
1 4 2
1 G1 4
1 G2 3
2 3 2
2 G2 1
3 4 2
3 G3 2
4 G1 3
G2 G1 1
G3 G2 2
输出样例1:
G1
2.0 3.3
输入样例2:
2 1 2 10
1 G1 9
2 G1 20
输出样例2:
No Solution