SVM (二)SVM理论基础
SVM的理论基础
上面我们讨论了关于 拉格朗日乘子法和KKT条件,下面我们讨论一下 SVM的一些基础概念。
我们从一个简单地二分类问题来看,给定 训练样本集合\( D =\{(x_1,y_1), (x_2,y_2),…, (x_m, y_m)\}, y_i \ \epsilon \ \{-1, +1\}\)如下图所示:
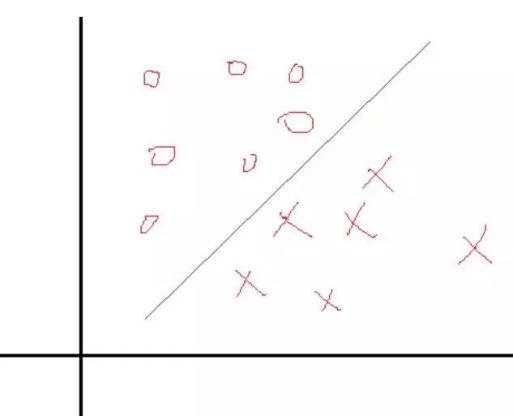
分类学习最基本的思想就是找到一个 超平面将不同的类别分开,因此我们希望找一个决策面使得两个类分开,那么决策面一般表示就是 \(W^T + b = 0\),现在的问题是如何找对应的W和b使得分割效果最好,这里跟logistic分类问题一样,也是找 权值。
在那里,我们使根据每一个样本的输出值和目标值得误差不断的调整权值W和b来求解。当然这种求解方式只是众多方式中的一种,那么SVM是怎么求最优的方式的呢?
这里我们反过来看,假设我们知道了结果,就是上面这样的分类线对应的权值W和b。那么我们会看到,在这两个类里面,是不是总能找到离这个线最近的点,像下面这样:
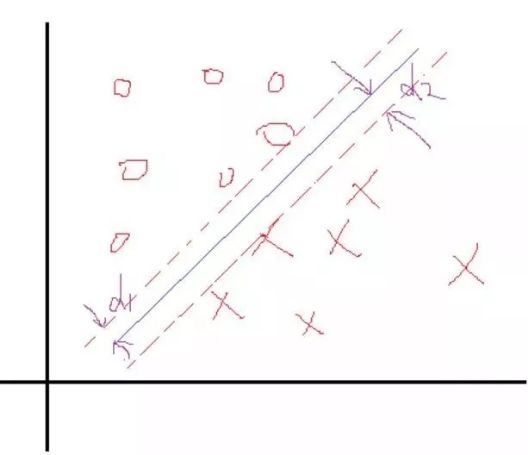
然后我们定义一下 离这条分类线的最近的点到这个分类面的距离分别为\(d_1\) 和 \(d_2\),因此我们知道总的距离就是\(D = (d_1 + d_2\),所以SVM的策略是 先找最边上的点,然后再找这两个距离之和D, 然后求解D的最大值。于是我们找到了这样的一个分界面\(W^T + b = 0\),那么做离它最近的两类点且平行于分类面,如上面的虚线所示。
W是这个超平面的法向量,决定了超平面的方向,b为位移项,决定了超平面与原点之间的距离。W和b唯一确定一个超平面。高中我们学过点到直线的距离公式,那么类比而得, 样本空间中样本点x到超平面的距离可以写为:
\begin{equation}
d = \frac{|W^Tx+b|}{||W||}
\end{equation}
确实不知道到底是几个单位,因此我们假设是k个单位,那么虚线就会变成\(W^T + b = k\),两边同除以k,那么虚线还是可以变成\(W^T + b = 1\)。然后中线就会变成\(W_1^T + b_1 = 0 \),可以看的出来,这中间就是一个 倍数的关系。
我们再来看\(D\)是怎么求的,假设分解面是\(W^T + b = 1\),我们从最简单的二维数据出发,假设X是二维数据,那么分类面可以写出来就是:\(w_1 x_1 + w_2 x_2 + b = 0\),初中知识,点到直线的距离就是\(d = \frac{1}{||W||}\),类比到平面可以得到,我们先假设向量\(W\)为\(W=(w1,w2)^T\),\(||W||\)是向量的第二范数,\(||W|| = \sqrt{W^T W}\),则距离D为:
\begin{equation}
D = d_1 + d_2 = \frac{2}{||W||}
\end{equation}
\begin{equation}
\begin{split}
& min \ \frac{1}{2}W^TW \\
& s.t. \ 1 - y_i (W x_i + b) \leq 0 ( y_i (W x_i + b) \geq 1)
\end{split}
\end{equation}
因此,我们引入 拉格朗日乘子法,优化的目标变为:
\begin{equation}
L(W,b,\alpha) = \frac{1}{2}W^T W + \sum_{i=1}^{m} \alpha_i(1 - y_i(W^T x_i + b))
\end{equation}
\begin{equation}
W = \sum_{i=1}^{m} \alpha_i y_i x_i
\end{equation}
\begin{equation}
0 = \sum_{i=1}^{m} \alpha_i y_i
\end{equation}
\begin{equation}
max \ \sum_{i=1}^{m}\alpha_i - \frac{1}{2} \sum \sum \alpha_i \alpha_j y_i y_j x_i^T x_j
\end{equation}
\begin{equation}
\begin{split}
s.t. &\sum_{i=1}^m \alpha_i y_i = 0 \\
&\alpha_i \geq 0 , \ i = 1,2,…,m
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\alpha_i \geq 0 \\
&1 - y_i f(x_i) \leq 0 \\
& \alpha_i (y_i f( x_i ) - 1) = 0
\end{split}
\end{equation}
\begin{equation}
\begin{split}
f(x) &= W^T x + b \\
& = \sum_{i=1}^m \alpha_i y_i x_i^T x + b
\end{split}
\end{equation}