图像处理---灰度变换

转自：https://www.cnblogs.com/wangguchangqing/p/6983680.html

前面几篇文章介绍的是图像的空间域滤波，其对像素的处理都是基于像素的某一邻域进行的。本文介绍的图像的灰度变换则不同，其对像素的计算仅仅依赖于当前像素和灰度变换函数。

灰度变换也被称为图像的点运算（只针对图像的某一像素点）是所有图像处理技术中最简单的技术，其变换形式如下：

s=T(r)s=T(r)

其中，T是灰度变换函数；r是变换前的灰度；s是变换后的像素。
图像灰度变换的有以下作用：

• 改善图像的质量，使图像能够显示更多的细节，提高图像的对比度（对比度拉伸）
• 有选择的突出图像感兴趣的特征或者抑制图像中不需要的特征
• 可以有效的改变图像的直方图分布，使像素的分布更为均匀

常见的灰度变换

灰度变换函数描述了输入灰度值和输出灰度值之间变换关系，一旦灰度变换函数确定下来了，那么其输出的灰度值也就确定了。可见灰度变换函数的性质就决定了灰度变换所能达到的效果。用于图像灰度变换的函数主要有以下三种：

• 线性函数 （图像反转）
• 对数函数:对数和反对数变换
• 幂律函数：n次幂和n次开方变换

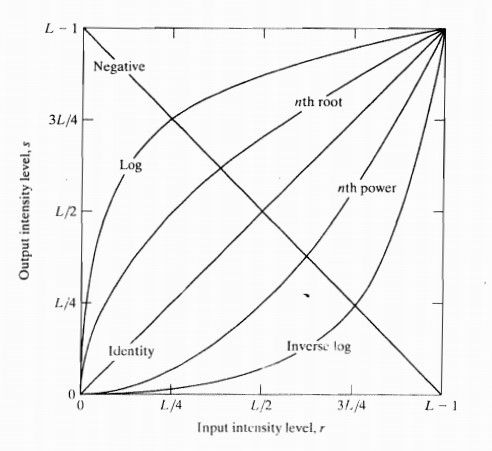
上图给出了几种常见灰度变换函数的曲线图，根据这几种常见函数的曲线形状，可以知道这几种变换的所能达到的效果。例如，对数变换和幂律变换都能实现图像灰度级的扩展/压缩，另外对数变换还有一个重要的性质，它能压缩图像灰度值变换较大的图像的动态范围（例如，傅立叶变换的频谱显示）。

线性变换

令r为变换前的灰度，s为变换后的灰度，则线性变换的函数：

s=a⋅r+bs=a⋅r+b

其中，a为直线的斜率，b为在y轴的截距。选择不同的a，b值会有不同的效果：

• a>1a>1，增加图像的对比度
• a<1a<1，减小图像的对比度
• a=1且b≠0a=1且b≠0，图像整体的灰度值上移或者下移，也就是图像整体变亮或者变暗，不会改变图像的对比度。
• a<0且b=0a<0且b=0，图像的亮区域变暗，暗区域变亮
• a=1且b=0a=1且b=0，恒定变换，不变
• a=−1且b=255a=−1且b=255，图像反转。

在进行图像增强时，上述的线性变换函数用的较多的就是图像反转了，根据上面的参数，图像反转的变换函数为：s=255−ss=255−s。图像反转得到的是图像的负片，能够有效的增强在图像暗区域的白色或者灰色细节。其效果如下：

图像反转的实现是比较简单的，在OpenCV中有对Mat的运算符重载，可以直接Mat r = 255 - img或者~img来实现。

对数变换

对数变换的通用公式是：

s=clog(1+r)s=clog⁡(1+r)

其中，c是一个常数，，假设 r≥0r≥0,根据上图中的对数函数的曲线可以看出：对数变换，将源图像中 范围较窄的低灰度值映射到范围较宽的灰度区间，同时将范围较宽的高灰度值区间映射为较窄的灰度区间，从而扩展了暗像素的值，压缩了高灰度的值，能够对图像中低灰度细节进行增强。；从函数曲线也可以看出，反对数函数的曲线和对数的曲线是对称的，在应用到图像变换其结果是相反的，反对数变换的作用是压缩灰度值较低的区间，扩展高灰度值的区间。
基于OpenCV的实现，其对数变换的代码如下：

float pixels[256];
    for (int i = 0; i < 256; i++)
        pixels[i] = log(1 + i);

    Mat imageLog(image.size(), CV_32FC3);
    for (int i = 0; i0; jVec3f>(i, j)[0] = pixels[image.at<Vec3b>(i, j)[0]];
            imageLog.at<Vec3f>(i, j)[1] = pixels[image.at<Vec3b>(i, j)[1]];
            imageLog.at<Vec3f>(i, j)[2] = pixels[image.at<Vec3b>(i, j)[2]];
        }
    }
    //归一化到0~255  
    normalize(imageLog, imageLog, 0, 255, CV_MINMAX);
    //转换成8bit图像显示  
    convertScaleAbs(imageLog, imageLog);

这使用的对数函数的底为10。由于灰度变换是灰度值之间的一对一的映射，而灰度值区间通常为[0,255]，所以在进行灰度变换时，通常使用查表法。也就是，现将每个灰度值的映射后的结果计算出来，在变换时，通过查表得到变换后的灰度值。执行上面结果得到的结果如下：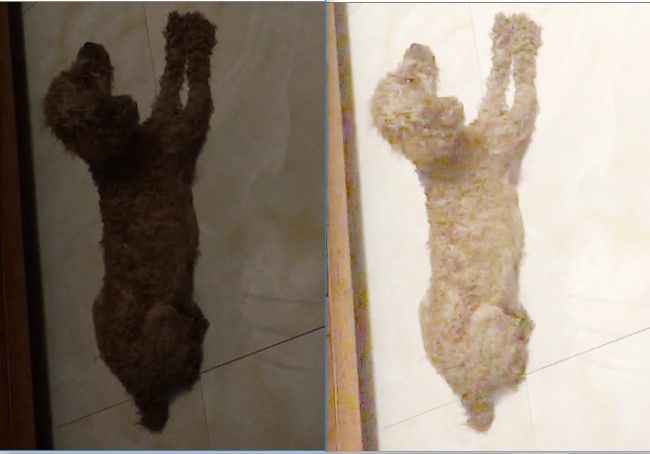

左边为原图像，其拍摄环境较暗，无法分辨出很多的细节；右边为变换后的图像，整个图像明亮许多，也能分辨出原图中处于暗区域的狗狗的更多细节。
对数变换，还有一个很重要的性质，能够压缩图像像素的动态范围。例如，在进行傅立叶变换时，得到的频谱的动态范围较大，频谱值的范围通常为[0,106][0,106]，甚至更高。这样范围的值，显示器是无法完整的显示如此大范围的灰度值的，因而许多灰度细节会被丢失掉。而将得到的频谱值进行对数变换，可以将其动态范围变换到一个合适区间，这样就能够显示更多的细节。

幂律变换（伽马变换）

伽马变换的公式为：

s=crγs=crγ

其中c和 γγ为正常数。
伽马变换的效果与对数变换有点类似，当 γ>1γ>1时将较窄范围的低灰度值映射为较宽范围的灰度值，同时将较宽范围的高灰度值映射为较窄范围的灰度值；当 γ<1γ<1时，情况相反，与反对数变换类似。其函数曲线如下：

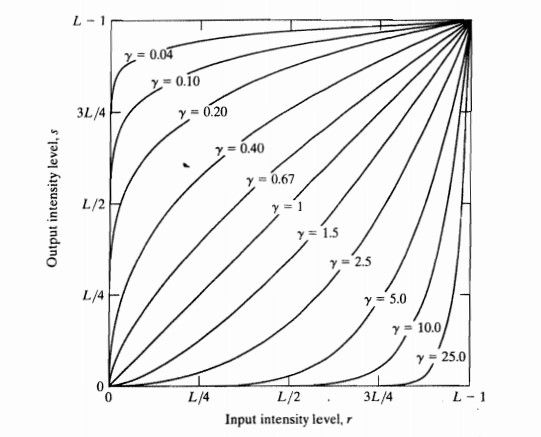
当γ<1γ<1时，γγ的值越小，对图像低灰度值的扩展越明显；当γ>1γ>1时，γγ的值越大，对图像高灰度值部分的扩展越明显。这样就能够显示更多的图像的低灰度或者高灰度细节。
伽马变换主要用于图像的校正，对灰度值过高（图像过亮）或者过低（图像过暗）的图像进行修正，增加图像的对比度，从而改善图像的显示效果。
基于OpenCV的实现：

float pixels[256];
    for (int i = 0; i < 256; i++)
        pixels[i] = i * i *i;

    Mat imageLog(image.size(), CV_32FC3);
    for (int i = 0; i0; jVec3f>(i, j)[0] = pixels[image.at<Vec3b>(i, j)[0]];
            imageLog.at<Vec3f>(i, j)[1] = pixels[image.at<Vec3b>(i, j)[1]];
            imageLog.at<Vec3f>(i, j)[2] = pixels[image.at<Vec3b>(i, j)[2]];
        }
    }
    //归一化到0~255  
    normalize(imageLog, imageLog, 0, 255, CV_MINMAX);
    //转换成8bit图像显示  
    convertScaleAbs(imageLog, imageLog);

这里选择的参数为c = 1,γ=3γ=3，来扩展图像的高灰度区域，其结果如下：

当选择参数为c = 1,γ=0.4γ=0.4,来扩展图像的低灰度区域，其效果如下：

根据以上的结果，结合伽马变换的函数曲线图，做如下总结：

• γ>1γ>1时，会将低于某个灰度值K的灰度区域压缩到较小的灰度区间，而将高于K的灰度区域扩展到较大灰度区间。令L为灰度的最大值，k = 3/4L . 那么就有[0,3/4L][0,3/4L]的灰度区域映射到为[0,1/8L][0,1/8L]的输出；而将[3/4L,L][3/4L,L]这部分高灰度区域映射到[1/8L,L][1/8L,L]区间。这样变换的结果就是，低于Ｋ的灰度区域被压缩到更低灰度区间，而较亮的高灰度区域的灰度值被扩展到较大的灰度区间变的不那么亮，整体的效果就是图像的对比度增加了，但是由于亮度区域被扩展，也就不那么亮了。
• γ<1γ<1时，会将灰度值较小的低灰度区域扩展到较宽的灰度区间，而将较宽的高灰度区域压缩到较小的灰度区间。这样变换的效果就是，低灰度区域扩展开来，变亮；而宽的高灰度区域，被压缩的较窄的区间，也变亮了，故变换后的整体效果是变亮了。

基于OpenCV的灰度变换实现

灰度变换属于点对点的一一变换，在实现的时候，可以利用查表法。也就是实现将[0,255]区间的各个灰度值的变换后的值计算出来，在变换的时候直接根据灰度值进行查表得到变换后的结果。其实现如下：

/////////////////////////////////////////////////////////////////////
//
// 灰度线性变换函数
// 参数：
//        src，输入原图像
//        dst,输出图像，类型为CV_32F，大小及通道数与原图像相同
//        mapping,灰度映射表，可以根据不同的变换函数，提前计算好图像的灰度映射表
//
////////////////////////////////////////////////////////////////////
void gray_trans(const Mat& src, Mat& dst,float* mapping)
{
    int channels = src.channels();
    if (channels == 1)
    { 
        dst = Mat(src.size(), CV_32FC1);
        for (int i = 0; i < src.rows; i++)
        {
            float* p1 = dst.ptr<float>(i);
            const uchar* p2 = src.ptr(i);
            for (int j = 0; j < src.cols; j++)
                p1[j] = mapping[p2[j]];
        }
    }
    else if (channels == 3)
    {
        dst = Mat(src.size(), CV_32FC3);
        for (int i = 0; i < src.rows; i++)
        {
            float* p1 = dst.ptr<float>(i);
            const uchar* p2 = src.ptr(i);
            for (int j = 0; j < src.cols * 3; j+=3)
            {
                p1[j] = mapping[p2[j]];
                p1[j+1] = mapping[p2[j+1]];
                p1[j+2] = mapping[p2[j+2]];
            }            
        }
    }
}

其调用也比较简单，根据具体的灰度变换函数，填充灰度映射表即可，以伽马变换为例：

    float pixels[256];
    for (int i = 0; i < 256; i++)
        pixels[i] = powf(i, 1.5);
    Mat imageLog;
    gray_trans(image, imageLog, pixels);

总结

本文主要对图像的几种常见的灰度变换进行了总结。

• 图像反转，是图像线性变换的一种，可以得到图像负片，能够有效的增强图像的暗色区域中的白色或者灰色细节
• 对数变换，扩展图像中的低灰度区域，压缩图像中的高灰度区域，能够增强图像中的暗色区域的细节；反对数变换与此相反。对数变换还有个重要作用是，能够压缩图像灰度值的动态范围，在傅立叶变换中能够显示更多的变换后的频谱细节。
• 伽马变换，主要用于图像的校正，根据参数γγ的选择不同，能够修正图像中灰度过高（γ>1γ>1）或者灰度过低（γ<1γ<1）