numpy学习基础篇（二）

图像操作

SciPy提供了一些处理图像的函数。它可以将图像从磁盘读入numpy数组，将numpy数组作为图像写入磁盘以及调整图像大小的功能。

from scipy.misc import imread,imsave,imresize

img=imread("E:\\Desktop\\894487.jpg")      #读取图片
print(img.dtype,img.shape)
img_tinted=img=img*[1,1,1]    #用了广播的方法，在图像的通道数这一维度进行了调整，三个通道分别对应红，绿，蓝
img_tinted=imresize(img_tinted,(500,500))  #将图像大小调整为500*500
imsave("E:/Desktop/8944871111.jpg",img_tinted)  #保存图片（路径，图片变量）

下图为img_tinted=img=img*[0,0,1] 尺寸（500,500）的变换图片

点之间的距离

SciPy定义了一下用于计算点集之间距离的有用函数。

函数scipy.spatial.distance.pdist计算给定集合中所有点对之间的距离：

from scipy.spatial.distance import pdist,squareform

x=np.array([[0,0],[0,1],[1,0],[1,1],[2,2]])
d=squareform(pdist(x,'euclidean'))  #euclidean表示欧式距离，不写默认为欧式距离
print(d)

result：
[[0.         1.         1.         1.41421356 2.82842712]
 [1.         0.         1.41421356 1.         2.23606798]
 [1.         1.41421356 0.         1.         2.23606798]
 [1.41421356 1.         1.         0.         1.41421356]
 [2.82842712 2.23606798 2.23606798 1.41421356 0.        ]]

Matplotlib

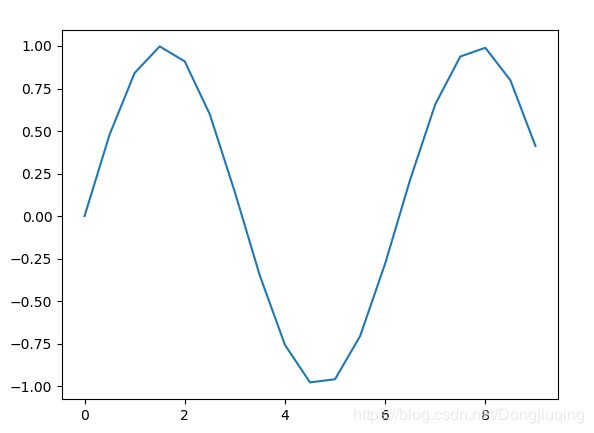
Matplotlib中最重要的是plot，可以用来绘制2D图像：

import matplotlib.pyplot as plt
x=np.arange(0,3*np.pi,0.5)
y=np.sin(x)
plt.plot(x,y)
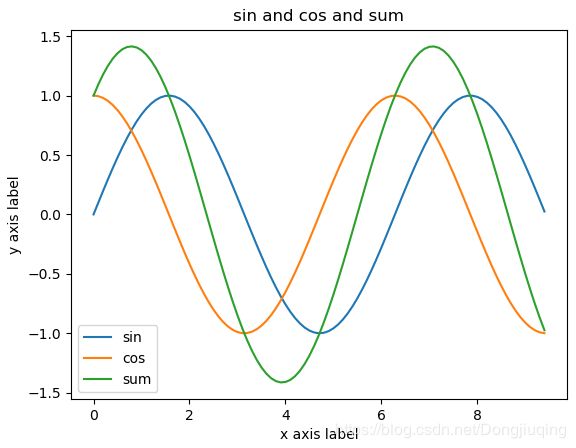
plt.show()

当然也可以在同一张图中一次绘制多条曲线，添加相应标题、标签。如上图右图所示。

import matplotlib.pyplot as plt

x=np.arange(0,3*np.pi,0.1)        #x的范围从0-3pi，间隔0.1长度读取元素。
y_sin=np.sin(x)
y_cos=np.cos(x)                    #设置变量
plt.plot(x,y_sin)
plt.plot(x,y_cos)
plt.plot(x,y_cos+y_sin)            #划线
plt.xlabel("x axis label")        #x轴信息
plt.ylabel("y axis label")        #y轴信息
plt.title("sin and cos and sum")    #标题栏
plt.legend(['sin','cos','sum'])    #标签栏
plt.show()              #展示图片

子图

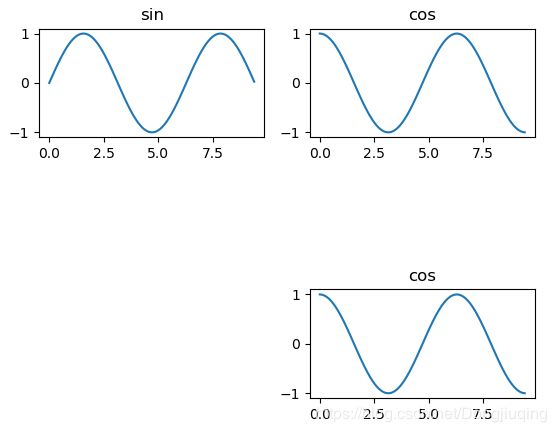
可以使用subplot函数在同一个图中绘制不同的东西。

#plt.subplot(x,y,z)  原图可容纳x*y个子图，这是第z个图，子图表现形式为x行y列，共x*y个

import matplotlib.pyplot as plt
x=np.arange(0,3*np.pi,0.1)
y_sin=np.sin(x)
y_cos=np.cos(x)
plt.subplot(3,2,1)   #创建子图（3,2,1）  原图可容纳6个子图，这是第1个图
plt.plot(x,y_sin)
plt.title("sin")
plt.subplot(3,2,2)   #创建子图（3,2,2）  原图可容纳6个子图，这是第2个图
plt.plot(x,y_cos)
plt.title("cos")
plt.subplot(3,2,6)
plt.plot(x,y_cos)
plt.title("cos")
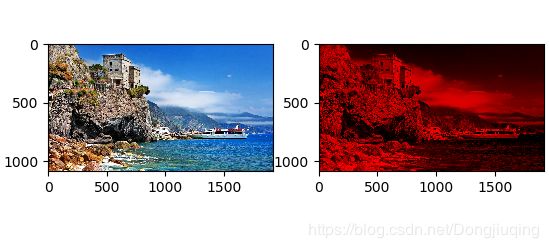
plt.show()

加载图片

你可以使用imshow函数来显示一张图片。

import matplotlib.pyplot as plt
from scipy.misc import imread,imresize

img=imread("E:\\Desktop\\894487.jpg")
img_tined=img*[1,0,0]
plt.subplot(1,2,1)
plt.imshow(img)
plt.subplot(1,2,2)
plt.imshow(img_tined)
plt.show()

用numpy求解方程组

线性代数比较常见的问题是求解矩阵向量方程。形如 Ax = b

如A为一个3*3的矩阵，b为3*1的向量。

A=np.array([[2,1,-2],[3,0,1],[1,1,-1]])
b=np.transpose(np.array([-3,2,-2]))
x=np.linalg.solve(A,b)     #求解方程组
print(x)