| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 人工智能实战2019 |
| 这个作业的要求在哪里 | 作业要求 |
| 我在这个课程的目标是 | 学会人工智能基本算法 |
| 这个作业在哪个具体方面帮助我实现目标 | 使用minibatch的方法进行梯度下降 |
第四章学习总结
最小二乘法,梯度下降法,神经网络法(本质上还是梯度下降法) 三种算法的目标都是求得使误差函数取得最小值的参数w,b。
最小二乘法实际上是数学上由多元函数求偏导算极限的方法。通过次方法可以精确的求得数学解析解。但它的缺点是并非对所有误差函数,都能通过解析的方法求解(例如高次方程没有公式解)。
梯度下降是同过给定的步长在每个点从下降最快的方向逼近误差函数的最小值。通过多次迭代直到求得满足精度要求的最优解。这个过程类似于牛顿下山法求解高次方程 。
使用minibatch的方法梯度下降代码
# Copyright (c) Microsoft. All rights reserved.
# Licensed under the MIT license. See LICENSE file in the project root for full license information.
# multiple iteration, loss calculation, stop condition, predication
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
import random
x_data_name = "TemperatureControlXData.dat"
y_data_name = "TemperatureControlYData.dat"
class CData(object):
def __init__(self, loss, w, b, epoch, iteration):
self.loss = loss
self.w = w
self.b = b
self.epoch = epoch
self.iteration = iteration
def ReadData():
Xfile = Path(x_data_name)
Yfile = Path(y_data_name)
if Xfile.exists() & Yfile.exists():
X = np.load(Xfile)
Y = np.load(Yfile)
return X.reshape(1, -1), Y.reshape(1, -1)
else:
return None, None
# 读取数据,np.load方法把数据以矩阵或向量的方式输出
def ForwardCalculationBatch(W, B, batch_x):
Z = np.dot(W, batch_x) + B
return Z
# 前向计算z=wx + b np.dot方法进行矩阵乘
def BackPropagationBatch(batch_x, batch_y, batch_z):
m = batch_x.shape[1]
dZ = batch_z - batch_y
dB = dZ.sum(axis=1, keepdims=True) / m
dW = np.dot(dZ, batch_x.T) / m
return dW, dB
# 反向计算dz = z - y, dw = (z - y)*x, db = z - y
def UpdateWeights(w, b, dW, dB, eta):
w = w - eta * dW
b = b - eta * dB
return w, b
# 根据步长更新参数w,b的取值
def InitialWeights(num_input, num_output, flag):
if flag == 0:
# zero
W = np.zeros((num_output, num_input))
elif flag == 1:
# normalize
W = np.random.normal(size=(num_output, num_input))
elif flag == 2:
# xavier
W = np.random.uniform(
-np.sqrt(6 / (num_input + num_output)),
np.sqrt(6 / (num_input + num_output)),
size=(num_output, num_input))
B = np.zeros((num_output, 1))
return W, B
# 初始化超参数
def ShowResult(X, Y, w, b, iteration):
# draw sample data
plt.plot(X, Y, "b.")
# draw predication data
PX = np.linspace(0, 1, 10)
PZ = w * PX + b
plt.plot(PX, PZ, "r")
plt.title("Air Conditioner Power")
plt.xlabel("Number of Servers(K)")
plt.ylabel("Power of Air Conditioner(KW)")
plt.show()
print("iteration=", iteration)
print("w=%f,b=%f" % (w, b))
def CheckLoss(W, B, X, Y):
m = X.shape[1]
Z = np.dot(W, X) + B
LOSS = (Z - Y) ** 2
loss = LOSS.sum() / m / 2
return loss
def RandomSample(X,Y,batchsize):
batch_x = np.zeros((1,batchsize))
batch_y = np.zeros((1,batchsize))
for i in range(batchsize):
r=random.randint(0,X.shape[1]-1)
batch_x[0,i] = X[0,r]
X = np.delete(X,i,axis=1)
batch_y[0,i] = Y[0,r]
Y = np.delete(Y,i,axis=1)
return batch_x, batch_y
# 通过随机的方式选取数据
def GetMinimalLossData(dict_loss):
key = sorted(dict_loss.keys())[0]
w = dict_loss[key].w
b = dict_loss[key].b
return w, b, dict_loss[key]
# 得到误差最小时取得w和b
def ShowLossHistory(dict_loss, method):
loss = []
for key in dict_loss:
loss.append(key)
# plt.plot(loss)
plt.plot(loss[30:800])
plt.title(method)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.show()
def loss_2d(x, y, n, dict_loss, method, cdata):
result_w = cdata.w[0, 0]
result_b = cdata.b[0, 0]
# show contour of loss
s = 150
W = np.linspace(result_w - 1, result_w + 1, s)
B = np.linspace(result_b - 1, result_b + 1, s)
LOSS = np.zeros((s, s))
for i in range(len(W)):
for j in range(len(B)):
w = W[i]
b = B[j]
a = w * x + b
loss = CheckLoss(w, b, x, y)
LOSS[i, j] = np.round(loss, 2)
# end for j
# end for i
print("please wait for 20 seconds...")
while (True):
X = []
Y = []
is_first = True
loss = 0
for i in range(len(W)):
for j in range(len(B)):
if LOSS[i, j] != 0:
if is_first:
loss = LOSS[i, j]
X.append(W[i])
Y.append(B[j])
LOSS[i, j] = 0
is_first = False
elif LOSS[i, j] == loss:
X.append(W[i])
Y.append(B[j])
LOSS[i, j] = 0
# end if
# end if
# end for j
# end for i
if is_first == True:
break
plt.plot(X, Y, '.')
# end while
# show w,b trace
w_history = []
b_history = []
for key in dict_loss:
w = dict_loss[key].w[0, 0]
b = dict_loss[key].b[0, 0]
if w < result_w - 1 or result_b - 1 < 2:
continue
if key == cdata.loss:
break
# end if
w_history.append(w)
b_history.append(b)
# end for
plt.plot(w_history, b_history)
plt.xlabel("w")
plt.ylabel("b")
title = str.format("Method={0}, Epoch={1}, Iteration={2}, Loss={3:.3f}, W={4:.3f}, B={5:.3f}", method, cdata.epoch,
cdata.iteration, cdata.loss, cdata.w[0, 0], cdata.b[0, 0])
plt.title(title)
plt.show()
def InitializeHyperParameters(method):
if method == "SGD":
eta = 0.1
max_epoch = 50
batch_size = 1
elif method == "MiniBatch":
eta = 0.1
max_epoch = 50
batch_size = 20
elif method == "FullBatch":
eta = 0.5
max_epoch = 1000
batch_size = 200
return eta, max_epoch, batch_size
if __name__ == '__main__':
# 修改method分别为下面三个参数,运行程序,对比不同的运行结果
# SGD, MiniBatch, FullBatch
method = "MiniBatch"
eta, max_epoch, batch_size = InitializeHyperParameters(method)
W, B = InitialWeights(1, 1, 0)
# calculate loss to decide the stop condition
loss = 5
dict_loss = {}
# read data
X, Y = ReadData()
# count of samples
num_example = X.shape[1]
num_feature = X.shape[0]
# if num_example=200, batch_size=10, then iteration=200/10=20
max_iteration = (int)(num_example / batch_size)
for epoch in range(max_epoch):
# 设置迭代次数
print("epoch=%d" % epoch)
for iteration in range(max_iteration):
# 根据batch_size确定循环次数
# get x and y value for one sample
batch_x, batch_y = RandomSample(X, Y, batch_size)
# get z from x,y
batch_z = ForwardCalculationBatch(W, B, batch_x)
# calculate gradient of w and b
dW, dB = BackPropagationBatch(batch_x, batch_y, batch_z)
# update w,b
W, B = UpdateWeights(W, B, dW, dB, eta)
# calculate loss for this batch
loss = CheckLoss(W, B, X, Y)
print(epoch, iteration, loss, W, B)
prev_loss = loss
dict_loss[loss] = CData(loss, W, B, epoch, iteration)
# end for
# end for
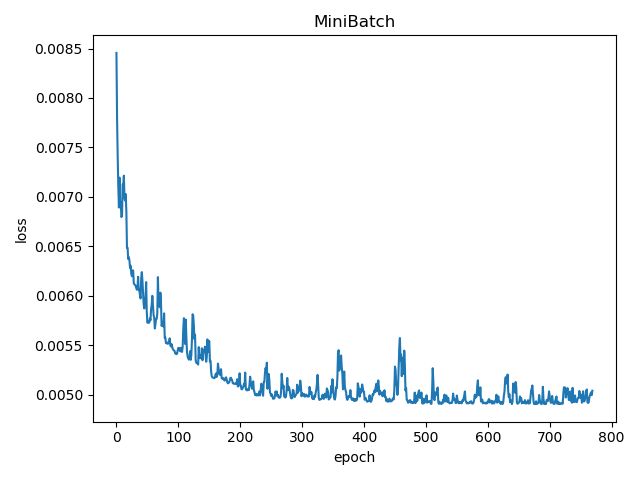
ShowLossHistory(dict_loss, method)
w, b, cdata = GetMinimalLossData(dict_loss)
print(cdata.w, cdata.b)
print("epoch=%d, iteration=%d, loss=%f" % (cdata.epoch, cdata.iteration, cdata.loss))
# ShowResult(X, Y, W, B, epoch)
print(w, b)
x = 346 / 1000
result = ForwardCalculationBatch(w, b, x)
print(result)
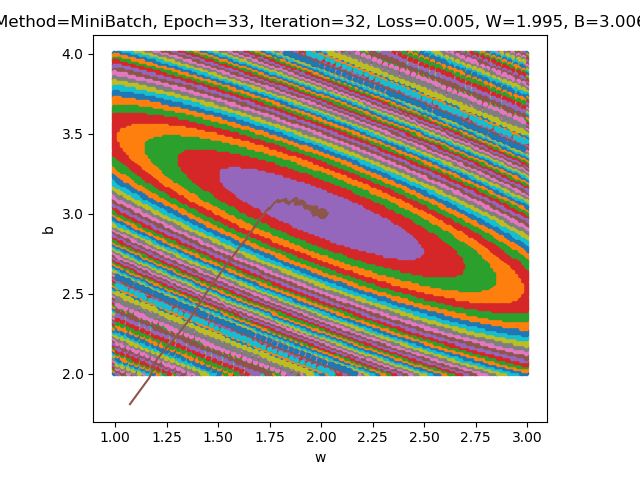
loss_2d(X, Y, 200, dict_loss, method, cdata)结果分析
- batch_size = 5
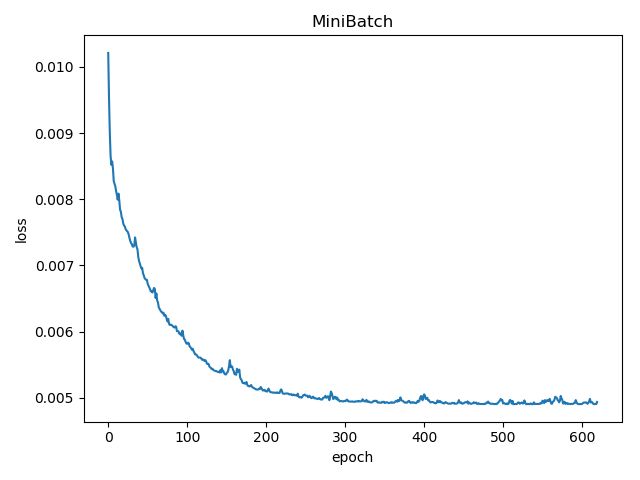
- batch_size = 10
- batch_size = 15
full_batch, SDG, mini_batch只是选取数据集的方式不同也即误差函数不同。比如mini_batch中每个batch_size对应的误差函数都是不一样的
mini_batch方法随着batch_size的增大,“毛刺”减少,所得的结果震荡幅度小,收敛性强,结果更精确。
为什么是椭圆不是圆
- 当图像为圆时说明w和b对误差函数的影响是一样的,因此z对w,b的偏导数应该相同。这是由数据集决定的,如果所给的数据能恰好满足这个关系,那么就可以是圆。
为什么中心是椭圆区域不是一个点
- 可类比地图中等高线的定义,等高线是不连续的,同一片颜色区域表示在同一个值附近。
- 由于误差函数随着迭代次数的增加,误差函数的变化越来越小,因此越靠近中间的区域,面积越大。