1.学习总结
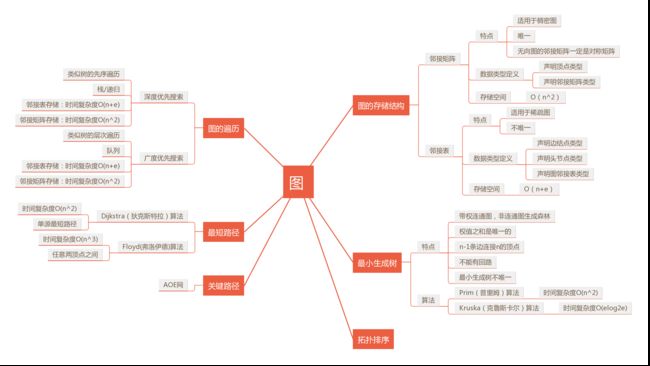
1.1图的思维导图
1.2 图结构学习体会
算法学习体会
1.深度遍历算法
①类似树的先序遍历,后进先出,借助栈或递归实现
②需设置一个visited[] 全局数组, visited[i]=0表示顶点i没有访问; visited[i]=1表示顶点i已经访问过。
2.广度遍历算法
①类似树的层次遍历,先进先出,借助队列实现
②需设置一个visited[] 全局数组, visited[i]=0表示顶点i没有访问; visited[i]=1表示顶点i已经访问过。
3.Prim和Kruscal算法
Prim算法(归并点):
①需设置2个辅助数组,closest[i]:边依附在U中顶点编号,lowcost[i]表示顶点i(i ∈ V-U)到U中顶点的边权重,取最小权重的顶点k加入U,并规定lowcost[k]=0表示这个顶点在U中;
②用邻接矩阵存储,适用于稠密图
③算法代码思路
- 初始化closest[i],lowcost[i]数组
- 遍历lowcost数组,选最小边
- 遍历lowcost数组,修正lowcost数组和closest数组
Kruscal算法(归并边):
①按权值的递增次序选择合适的边来构造最小生成树
②用邻接表存储,适用于稀疏图
③算法过程
(1)置U的初值等于V(即包含有G中的全部顶点),TE的初值为空集(即图T中每一个顶点都构成一个连通分量)。
(2)将图G中的边按权值从小到大的顺序依次选取: 若选取的边未使生成树T形成回路,则加入TE; 否则舍弃,直到TE中包含(n-1)条边为止。
对Kruscal算法的代码实现还未完全掌握
4.Dijkstra算法
①适用于单源最短路径,即一顶点到其余各顶点
②带权有向图,带权无向图均适用
③需设置数组s[i]标记已找到最短路径的顶点,一维数组dist[j]存储目前最短路径长度,一维数组path[j]存储最短路径,保存当前路径中前一个顶点的编号
④算法特点
- 不适用带负权值的带权图求单源最短路径
- 不适用求最长路径长度
- 最短路径长度是递增
- 顶点u加入S后,不会再修改源点v到u的最短路径长度
⑤算法代码思路
- 初始化disth数组、path数组
- 遍历图中所有顶点,找最小路径长度顶点u,最短路径dist
- 修正dist
- 输出最短路径
5.拓扑排序算法
①有向无环图,可以用来检测图中是否有回路
②需在表头结点中增加一个存放顶点入度的域count;入度减1实现连接边删除
③拓扑排序方法
1.从有向图中选取一个没有前驱的顶点,并输出之;
2.从有向图中删去此顶点以及所有以它为尾的弧;
3.重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止。
④算法代码思路
- 遍历邻接表 计算每个顶点的入度,存入头结点count成员
- 遍历图顶点 若发现入度为0顶点,入栈st
- 遍历v的所有邻接点
2.PTA实验作业(4分)
题目1: 六度空间
2.2 设计思路(伪代码或流程图)
定义变量first 表示队头指针,rear表示队尾指针,count表示统计人数,level,表示层数,last表示这一层访问的最后一个节点
初始化 count = 1,level = 0,last = v
入队 queue[++rear] = v
while(队列不空时进入循环)
出队 dequeue = queue[++first]
for i=0 to 人数
{ if(此结点未被访问)
标记已访问,对当前结点入队,并将层数加1
}
若上一层最后一个顶点弹出了
则层数递增
当六层遍历结束,退出搜索
返回 count
2.3 代码截图
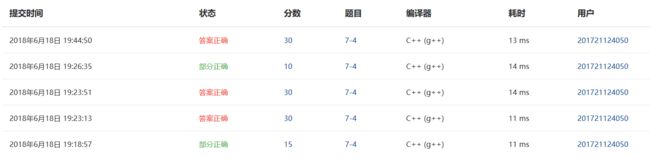
2.4 PTA提交列表说明
问题1:答案错误
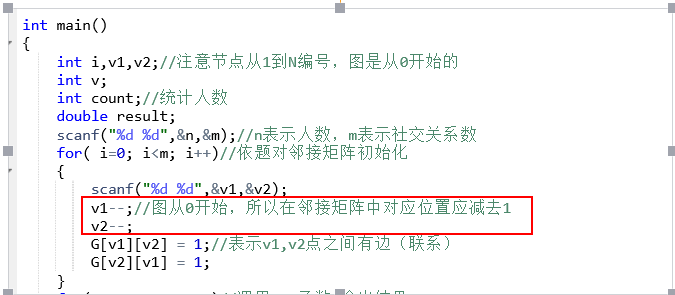
经检查发现在依题对邻接矩阵初始化过程中,未注意到节点从1到N编号,而图是从0开始的
改正前
解决:在邻接矩阵中对应位置应减去1
改正后
部分正确
问题:未注意在六层遍历后,退出,导致答案错误
错误部分截图
解决:增加一个判断条件,在level==6时,退出循环
改正后代码截图
题目2:旅游规划
2.2 设计思路(伪代码或流程图)
min函数
定义dist[s]=0表示目前最短路径长度 ,visited[s]=1标记表示编号为s的点加入visited中
for i=0 to 城市数
若该点未被访问且目前最短路径长度小于最小长度初值
则置最小长度为目前最短路径长度
令visited[s]=1,表示顶点s加入visited中
for j=0 to 城市数
若s点未被访问且经过s点到目标点的距离小于原本最短路径长度
则修改当前路径长度和当前费用
若距离等长且此路费用少于原本费用
修改当前费用
2.3 代码截图
2.4 PTA提交列表说明
部分正确提示错误截图
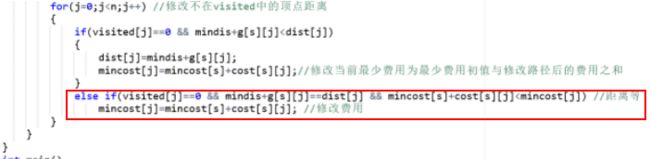
问题:未考虑路径等长时,费用少时则需更新费用
解决:增加一个判断条件当距离等长且此路费用少于原本费用 ,更新费用
题目3:公路村村通
2.2 设计思路(伪代码或流程图)
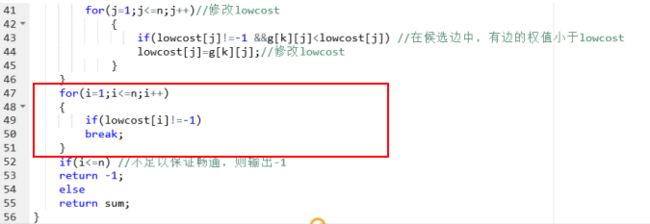
定义n表示城镇数目,sum表示总成本,lowcost表示当前最低成本,k表示记录最近顶点编号
for i=1 to n
for j=1 to n
若路畅通且费用少于当前最少费用
修改最少费用并改变k为最近顶点编号
令sum=sum+lowcost[k],计算当前顶点下的成本
若其他路的成本小于当前最低成本lowcost
修改最低成本lowcost
若不足以保证畅通,则输出-1 ,否则返回 sum
2.3 代码截图
2.4 PTA提交列表说明
错误点PTA截图
问题:循环条件错误
解决:将j=0修改为j=1
错误点PTA截图
问题:少了判断了一个条件
解决:增加判断不畅通时,跳出循环
3.截图本周题目集的PTA最后排名
3.1 PTA排名(截图带自己名字的排名)
3.2 我的总分:2分
4. 阅读代码
【题目介绍】:
所谓农夫过河问题是指农夫带一只狼、一只羊和一棵白菜在河南岸需要安全运到北岸。一条小船只能容下他和一件物品只有农夫能撑船。问农夫怎么能安全过河。
当然,狼吃羊,羊吃白菜,农夫不能将这两种或三种物品单独放在河的一侧,因为没有农夫的照看狼就要吃羊,而羊可能要吃白菜? 这类问题的实质是系统的状态问题, 要寻求的是从初始状态经一系列的安全状态到达系统的终止状态的一条路径。
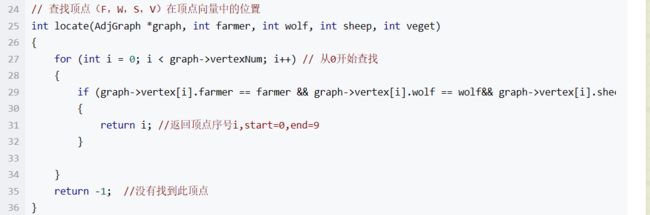
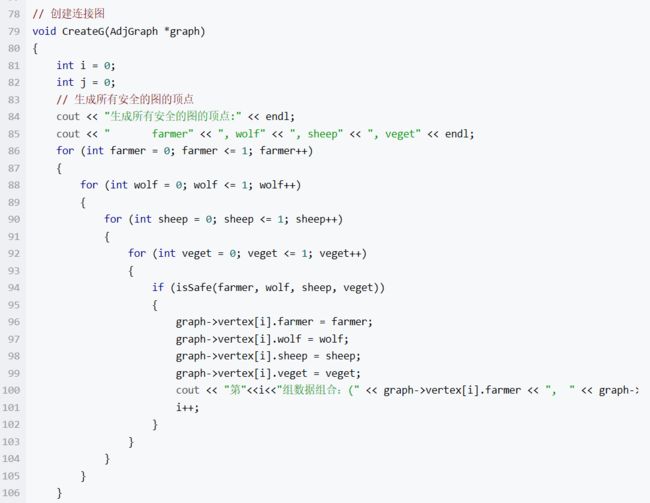
代码思想:
1、有16种组合。
2、判断待在同一边是否安全,得到10种组合,相当于10个顶点。
3、再根据谁要跟农夫过河得到所有可能的路径组合
4、第一个顶点和最后一个顶点已经确定,可遍历出最后的路径顺序。
学习的地方:
学会将实际问题抽象为数学模型,过河与没过河是两种不同的状态,农夫、狼、羊和菜,分别处于这两种状态,所以一共有2的4次方,16种状态。但这16种状态中有一些状态是不安全的应该剔除掉。 如果我们将没过河状态看做0,过河看做1,那么问题就变成从初始状态(0000),经过一定和有限个状态变成最终状态(1111)的过程。这样我们就可以抽象出一张图来,每个状态表示一个节点,满足条件的节点之间有一条路,这样问题就抽象为,在无向图中找一条路。