哈夫曼编码解码实现

                 关于哈夫曼编码只说一句理论的话（其他就当锻炼自己的Google能力）：哈夫曼树─即最优二叉树，带权路径长度最小的二叉树，经常应用于数据压缩。

         

这里直接上代码，代码中包括了自根节点向下和自叶子节点向上的编码，还有解码的实现。

huffmantree.h

/*------------------------------------------------------------
	* file:huffmantree.h -->head file for HuffmanTree.c
	* date:10-6-2014
	* author:[email protected]
	* version:1.0
	* description:赫夫曼编码
--------------------------------------------------------------*/


typedef struct HTNode{
	unsigned int weight;
	char ch;
	unsigned int parent,lchild,rchild;

}*HuffmanTree;

typedef char **HuffmanCode;

#define LIMIT_MAX 256	//规定权值不能超过256(纯属个人喜好)




//在i个节点中找到权值最小的
int min(HuffmanTree *HT,int i);

//在i个节点中找到两个最小的
void Select(HuffmanTree *HT,int i,int *s1,int *s2);

//哈夫曼建树和编码
void HuffmanCoding(HuffmanTree *HT,HuffmanCode *HC,int *w,char *str,int n);


//哈夫曼建树和编码
void HuffmanCoding_1(HuffmanTree *HT,HuffmanCode *HC,int *w,int n);


//解码
void HuffmanDecode(HuffmanTree HT,char *code,char *str,int n);

代码的注释非常详细了

HuffmanTree.c

/*------------------------------------------------------------
	* file:HuffmanTree.c
	* date:10-7-2014
	* author:[email protected]
	* version:1.2
	* description:赫夫曼编码(自下向上和自上向下编码)
	* more:增加了解码功能
--------------------------------------------------------------*/





#include 
#include 
#include "huffmantree.h"

/*
* @description:建立Huffman树，并对所给的权值进行哈夫曼编码(从叶子节点向上到根节点进行编码)
*/

void HuffmanCoding(HuffmanTree *HT,HuffmanCode *HC,int *w,char *str,int n) {

	int i,c,f,m,s1,s2,start;
	HuffmanTree p;
	char *cd;

	if(n <= 1)
		return;
	//如果哈夫曼有n个叶子节点(即有n个字符需要进行哈夫曼编码),则因整棵树有2*n -1个节点
	m = 2 * n - 1; 

	//这里之所以要到申请一个是因为方便处理，第0个永远不会用到,初始化时父亲和孩子指针都指向它
	*HT = (HuffmanTree)  malloc( (m+1) * sizeof(struct HTNode));

	//把权值匹配给前n个节点
	for(p = HT + 1,i = 1;i <= n ; i++,p++,w++,str++) {
		(*HT)[i].weight = *w;
		(*HT)[i].ch = *str;
		(*HT)[i].parent = 0;
		(*HT)[i].lchild = 0;
		(*HT)[i].rchild = 0;
	}

	//初始化剩余节点
	for(; i <= m;i++) {
		(*HT)[i].weight = 0;
		(*HT)[i].ch = '\0';
		(*HT)[i].parent = 0;
		(*HT)[i].lchild = 0;
		(*HT)[i].rchild = 0;
	}


	/*
	建立哈夫曼树
	*/
	for(i = n + 1; i <= m; i++) {
		//找到两个最小的权值根节点
		Select(HT,i-1,&s1,&s2);
		
		//两最小节点变成当前节点的左右孩子，当前节点为其父亲，权值为两节点的权值和
		(*HT)[s1].parent = i;
		(*HT)[s2].parent = i;

		(*HT)[i].lchild = s1;
		(*HT)[i].rchild = s2;

		(*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
	}

	/*
	进行哈夫曼编码
	*/

	//为每个字符编码的字符串分配头指针,之所以多一个为方便和HT处理相同的i值
	*HC = (HuffmanCode) malloc( (n+1) * sizeof(char *));
	//为每个字符的编码分配暂存存储空间,这里的n不一定会被用完
	cd = (char *) malloc(n * sizeof(char));

	//编码结束标志
	cd[n-1] = '\0';

	//正式开始编码
	for(i =1;i <= n; i++) {
		start = n-1;

		//这里的编码是从叶子节点向上到根节点进行的,往左则为0，往右则为1
		for(c = i,f = (*HT)[i].parent; f != 0;c = f, f = (*HT)[f].parent ) {
			if((*HT)[f].lchild == c)
				cd[--start] = '0';
			else
				cd[--start] = '1';
		}

		//申请实际需要的存储空间
		(*HC)[i] = (char *) malloc( (n-start) * sizeof(char) );
		//复制
		strcpy((*HC)[i],&cd[start]);

	}
	
	//释放暂存空间
	free(cd);
}





/*
* @description:建立Huffman树，并对所给的权值进行哈夫曼编码(从根节点向下到叶子节点进行编码)
*/

void HuffmanCoding_1(HuffmanTree *HT,HuffmanCode *HC,int *w,int n) {

	int i,c,cdlen,m,s1,s2,count;
	HuffmanTree p;
	char *cd;

	if(n <= 1)
		return;
	//如果哈夫曼有n个叶子节点(即有n个字符需要进行哈夫曼编码),则因整棵树有2*n -1个节点
	m = 2 * n - 1; 

	//这里之所以要到申请一个是因为方便处理，第0个永远不会用到,初始化时父亲和孩子指针都指向它
	*HT = (HuffmanTree)  malloc( (m+1) * sizeof(struct HTNode));

	//把权值匹配给前n个节点
	for(p = HT + 1,i = 1;i <= n ; i++,p++,w++) {
		(*HT)[i].weight = *w;
		(*HT)[i].parent = 0;
		(*HT)[i].lchild = 0;
		(*HT)[i].rchild = 0;
	}

	//初始化剩余节点
	for(; i <= m;i++) {
		(*HT)[i].weight = 0;
		(*HT)[i].parent = 0;
		(*HT)[i].lchild = 0;
		(*HT)[i].rchild = 0;
	}


	/*
	建立哈夫曼树
	*/
	for(i = n + 1; i <= m; i++) {
		//找到两个最小的权值根节点
		Select(HT,i-1,&s1,&s2);
		
		//两最小节点变成当前节点的左右孩子，当前节点为其父亲，权值为两节点的权值和
		(*HT)[s1].parent = i;
		(*HT)[s2].parent = i;

		(*HT)[i].lchild = s1;
		(*HT)[i].rchild = s2;

		(*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
	}

	/*
	进行哈夫曼编码
	*/

	//为每个字符编码的字符串分配头指针,之所以多一个为方便和HT处理相同的i值
	*HC = (HuffmanCode) malloc( (n+1) * sizeof(char *));
	//为每个字符编码后的字符串分配暂存空间
	cd = (char *) malloc(n * sizeof(char));
	
	//由于前面树已经建立起来，故可以用weight来做状态标志
	for(i = 1; i <= m; i++)
		(*HT)[i].weight = 0;

	c = m;
	cdlen = 0;
	count = 0;
	//注意这里的第m+1个节点即为根节点
	while(c) {
		//等于0说明该节点没有访问过
		if((*HT)[c].weight == 0) {
			//标记已经走过
			(*HT)[c].weight = 1;
			//往左走
			if((*HT)[c].lchild != 0) {
				c = (*HT)[c].lchild;
				cd[cdlen++] = '0';
			}
			//说明当前节点已经是叶子节点了，则将暂存空间的字符串复制
			else if((*HT)[c].rchild == 0) {
				//加一的空间用来存储'/0'
				(*HC)[++count]  = (char *) malloc( (cdlen + 1) * sizeof(char));
				cd[cdlen] = '\0';
				strcpy((*HC)[count],cd);
			}
		}
		//等于1说明已经访问过该节点了
		else if((*HT)[c].weight == 1) {
			(*HT)[c].weight = 2;
			//往右走
			if((*HT)[c].rchild != 0) {
				c = (*HT)[c].rchild;
				cd[cdlen++] = '1';
			}
		}
		//等于2说明该节点已经是叶子节点且编码已经完成了
		else if((*HT)[c].weight == 2){
			//往回走，直到根节点
			(*HT)[c].weight = 0;
			c = (*HT)[c].parent;
			--cdlen;
		}
	}

	//释放暂存空间
	free(cd);
}






/*
* @decription:在1--i个节点中找到权值最小的,这里类似于在数组中找最小值
*/
int min(HuffmanTree *HT,int i) {
	int k,j,flag;
	//预设一个最大值
	k = LIMIT_MAX;	
	
	for(j = 1;j <= i; j++)
		if((*HT)[j].weight < k && (*HT)[j].parent == 0) {
			k = (*HT)[j].weight;
			flag = j;
		}
	
	(*HT)[flag].parent = 1;

	return flag;
}


/*
* @description:从所有的节点(1 -- i个节点)找出根节点的权值最小的两个(且前面没有找过的即parent == 0)
*/
void Select(HuffmanTree *HT,int i,int *s1,int *s2) {
	int j;

	*s1 = min(HT,i);
	*s2 = min(HT,i);

	//要保证s1为两个中序号最小的
	if(*s1 > *s2) {
		j = *s1;
		*s1 = *s2;
		*s2 = j;
	}
}


/*
* @description:对已经给定的树和二进制码进行哈夫曼解码
*/
void HuffmanDecode(HuffmanTree HT,char *code,char *str,int n) {
	char *ch;
	ch = code;
	int i,m,j;

	m = 2 * n - 1; 
	j = 0;

	while(*ch != '\0') {
		//每次从根节点开始，往左右孩子找,'0'则为左,'1'则为右
		for(i = m; HT[i].lchild != 0 && HT[i].rchild != 0;) {
			if(*ch == '0')
				i = HT[i].lchild;
			else if(*ch == '1')
				i = HT[i].rchild;

			ch++;
		}

		//到叶子节点后将其字符值返回
		*(str + j) = HT[i].ch;
		j++;
	}
}

测试程序：

test.c

/*------------------------------------------------------------------
	* file:test.c -->test file fot HuffmanTree.c
	* date:10-7-2014
	* author:[email protected]
	* version:1.2
	* description:赫夫曼树的编码和解码
	* more:这里没有做输入检测，个数应该对应，有需要的自己增加检测
-----------------------------------------------------------------------*/

#include 
#include "huffmantree.h"

int main(int argc,char *argv[]) {
	int *w;
	char c;
	char *str,*arr;
	char code[100];
	int i,n,j;
	HuffmanTree HT;
	HuffmanCode HC;

	j = 0;

	//输入预定个数
	printf("please enter the number of total weigth:");
	scanf("%d",&n);

	w = (int *) malloc(n * sizeof(int));
	str = (char *) malloc(n * sizeof(char));
	arr = (char *) malloc(n * sizeof(char));

	//输入权
	printf("please enter the weights:\n");
	for(i = 0;i < n;i++)
		scanf("%d",w + i);

	//输入权值对应字符
	printf("please enter the str:\n");
	for(i = 0;i < n;) {
		if( (c = getchar()) != '\n') {
			*(str + i) = c;
			i++;
		}
	}

	//编码
	HuffmanCoding(&HT,&HC,w,str,n);
	
	//输出编码后的结果
	printf("\nthe result after coding:\n");
	//相对puts来说fputs会更加安全
	for(i = 1;i <= n;i++) {
		printf("%c:",*(str + i - 1));
		fputs(HC[i],stdout);
		printf("\n");
	}

	//输入需要解码的二进制数
	printf("\nplease enter the code to decode,enter # to end the input:");
	while( (c = getchar()) != '#') {
		code[j] = c;
		j++;
	}

	code[j] = '\0';

	//解码
	HuffmanDecode(HT,code,arr,n);

	//输出解码结果
	while(*arr != '\0')  {
		printf("%c",*arr);
		arr++;
	}

	printf("\n");

	return 0;


	/*
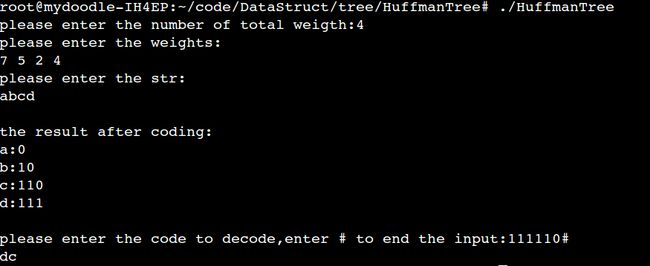
	测试结果：
	4
	7 5 2 4
	>>
	0
	10
	110
	111
	*/
}

完整代码:GitHub