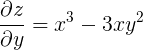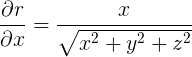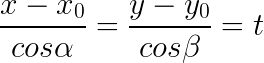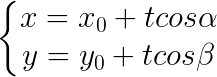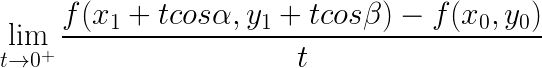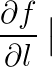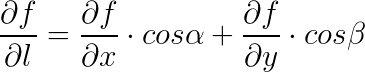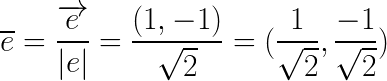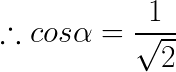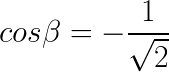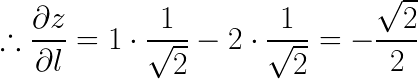梯度下降算法【从简单的数学的角度理解】Gradient Descent、偏导数、多元函数微分学

本篇博文，从简单的微积分作为切入点，介绍梯度下降的一些数学的基础理论。

本篇文章适合已经有了部分梯度下降算法的了解或者应用，想要从简单的数学基础去更深入学习该算法的童鞋

前置知识：微积分(多元函数微分、偏导数)

在正式进入主题之前，先补充一点微积分的基础知识

偏导数

定义：设函数   在区间  的某一领域内有定义，当  固定在 时，而  在  处有增量  时，相应的函数有增量：

如果：

  极限存在，那么就称此极限为 函数  在点  对  的偏导数

偏导数记作：

                                   或     

借一张图，解释偏导数的几何意义：

通过上面的这一张图，可以这么理解偏导数：有一个三维的坐标系 ，其中  是自变量，  是因变量。

即  ，那么： 意为 在固定 (上图是y=1)值的情况下，自变量  增加  (此处的是一个非常小的值，无限的趋近于0) 此时函数  的增量就是所谓的偏导数。

关于偏导数是否存在：这里不做过多的讨论，记住常见的场景：如果函数不连续那么偏导数不存在。但是反过来：偏导数存在函数不一定连续。这里不予以证明，想要了解更多的细节可以参考《微积分》

如何计算？

通过前面的一些知识铺垫，现在可以通过几个例子了解偏导数的计算

1.  , 求函数分别关于 、 的偏导数

2.求  的偏导数

当对某一变量求偏导数时，只需要把其他的变量看出常数，然后求导即可

1.   关于  的偏导数：  ， 关于  的偏导数：   

求关于  的偏导数时只需要把  看出常数，然后求导即可，同理即可求关于  的偏导数。

 

2、如果没有指明要关于哪一个自变量的偏导数，那么就是要求关于全部自变量的偏导数

像这样的复合函数求偏导数，可以先用变量  =   替代，所以有：

       先对  求导，然后乘以  对  的偏导数。ps 如果这里看不懂可能是基础弱，建议看看高中的导数>>>复合函数求导有的地方也叫链式求导。

     

   ，  又      

最终： ，

根据上面的计算流程同理可以计算出：

这里有函数对称性的定义，就说如果函数表达式中任意两个自变量对调后，任然是原来的函数那么这个函数就是对称的，对不同的自变量求偏导数的结果是一致的，只需要替换对应的变量符合，可以参考上面一题的结果。

通过上面的例子计算，相信童鞋们可以去试着推导一下，线性回归算法中应用梯度下降所求的梯度。

关于方向导数和梯度

了解完了偏导数和简单的偏导数计算，终于可以进入主题了.......

偏导数反应的是函数沿着坐标轴方向的变化率，但实际工程应用中，我们仅考虑坐标轴的变化率显然是不够的，因此我们有必要来讨论函数沿着特定方向的变化率问题，也就是所谓的 “方向导数“

设直线方程  是平面  上以点  为起点的一条射线， 是与这条射线同方向的单位向量,如下图所示：

那么我们已经知道  就是 直线方程  的方向向量，根据>>>>>>>向量代数与空间解析几何>>>>>直线的对称方程或点向式方程可以得：

                                                                   

所以，关于 直线方程  的参数方程为：

                                                                

有另外一个点  在直线  上，并且  与  两点直接的距离  ，如果极限：

                                                

存在，那么就把这个极限称为函数  在 点  处沿方向  的方向导数。用符号记作：

                                                                                             

这个符号看起来和求偏导数的符合是一样的，但是注意 这里的  是函数符号，不是某一个自变量符号。可以看成是函数对函数的偏导数。

方向导数如何计算？

方向导数计算有如下定量(此处不予以证明)：

                                                      

 与  就是方向  的方向余弦

 

1. 求函数  以点  为起点，移动到点  的方向导数 

分析：首先根据公式，首先需要求得 函数   关于 、 的偏导数，然后再求  、，前面提到过了偏导数的计算方法，相对来说是比较简单的。而   、 就是单位向量 。根据两个点就可以计算出沿此方向的单位向量，也是高中的数学知识，如果不清楚了度娘问一下。

                                  

单位向量   ：

         

      

把上述计算的结果代入到计算方向导数定义公式中，即可得：

这就是最终求得的方向导数

梯度

梯度是与方向到时有相关联的，在二元函数的情况下，设函数  在平面区域内有连续的一阶偏导数，那么对于每一个点  都可以定义出一个向量：

                                                  

这个向量就称为函数  在点  的梯度，记作  或 

可以看出，函数的梯度与函数方向导数定义式非常相接近， 其中 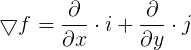 称作二维函数的向量微分算子或Nabla算子

回忆函数的方向导数定义式：

                                                 

因此有：

                                                      

其中  (这里指的是，函数梯度与单位方向向量夹角的余弦值)

上述结果说明了，当  时，说明函数梯度与方向相反，此时函数  减少的最快，对应到梯度下降法的下降，这也就是为什么我们更新梯度的时候是 “减”。

函数  的梯度向量是该函数在方向上取得最大值或者最小值，而梯度向量的模就等于方向导数的最大值或者最小值。

 

上述的全部例子都是在二维、三维的基础上进行介绍的，可以推广到多维空间上，定理任然成立。

 

好了，本篇博文就分享到这里，如果有疑问欢迎留言