sklearn实战:乳腺癌检测(逻辑回归算法)
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np# 载入数据
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X = cancer.data
y = cancer.target
print('data shape: {0};target shape: {1} no. positive: {2}; no. negative: {3}'.format(
X.shape, y.shape,y[y==1].shape[0], y[y==0].shape[0])) #shape[0]就是读取矩阵第一维度的长度
print(cancer.data[0]) #打印一组样本数据
data shape: (569, 30);target shape: (569,) no. positive: 357; no. negative: 212
[1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
4.601e-01 1.189e-01]
569个样本,30个特征,357个正样本(阳性)
print(len(cancer.feature_names))
cancer.feature_names30
array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension',
'radius error', 'texture error', 'perimeter error', 'area error',
'smoothness error', 'compactness error', 'concavity error',
'concave points error', 'symmetry error',
'fractal dimension error', 'worst radius', 'worst texture',
'worst perimeter', 'worst area', 'worst smoothness',
'worst compactness', 'worst concavity', 'worst concave points',
'worst symmetry', 'worst fractal dimension'], dtype='分成训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 模型训练
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(X_train, y_train)
train_score = model.score(X_train, y_train)
test_score = model.score(X_test, y_test)
print('train score: {train_score:.6f}; test score: {test_score:.6f}'.format(
train_score=train_score, test_score=test_score))train score: 0.960440; test score: 0.956140
# 样本预测
y_pred = model.predict(X_test)
# np.equal(y_pred, y_test)
print('matchs: {0}/{1}'.format(np.equal(y_pred, y_test)[np.equal(y_pred, y_test)==True].shape[0], y_test.shape[0]))
#np.equal比较的是值,而不是类型,返回bool。https://docs.scipy.org/doc/numpy/reference/generated/numpy.equal.htmlmatchs: 109/114
# 预测概率:找出(自信度)低于 90% 概率的样本个数
y_pred_proba = model.predict_proba(X_test) #计算测试数据的预测概率
print('sample of predict probability: {0}'.format(y_pred_proba[0]))
#打印第一个样本的概率数据
y_pred_proba_0 = y_pred_proba[:, 0] > 0.1
# y_pred_proba_0 bool型数组
result = y_pred_proba[y_pred_proba_0]
# result
y_pred_proba_1 = result[:, 1] > 0.1
print(result[y_pred_proba_1])sample of predict probability: [9.99986666e-01 1.33339531e-05]
[[0.67569183 0.32430817]
[0.87816535 0.12183465]
[0.28873244 0.71126756]
[0.37854579 0.62145421]
[0.80482984 0.19517016]
[0.4469654 0.5530346 ]
[0.89426703 0.10573297]
[0.17490112 0.82509888]
[0.27649555 0.72350445]
[0.34531035 0.65468965]
[0.63026927 0.36973073]
[0.28659955 0.71340045]
[0.80502091 0.19497909]
[0.20056432 0.79943568]
[0.73144372 0.26855628]]
- 模型优化:
- 增加多项式特征
- 使用正则项
import time
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
# 增加多项式预处理
def polynomial_model(degree=1, **kwarg):
polynomial_features = PolynomialFeatures(degree=degree,
include_bias=False)
logistic_regression = LogisticRegression(**kwarg)
pipeline = Pipeline([("polynomial_features", polynomial_features),
("logistic_regression", logistic_regression)])
return pipeline
model = polynomial_model(degree=2, penalty='l1') #二阶多项式决策边界,l1正则筛选重要关联特征
start = time.clock() #测量CPU时间,比较精准,通过比较程序运行前后的CPU时间差,得出程序运行的CPU时间
model.fit(X_train, y_train)
train_score = model.score(X_train, y_train)
cv_score = model.score(X_test, y_test)
print('elaspe: {0:.6f}; train_score: {1:0.6f}; cv_score: {2:.6f}'.format(
time.clock()-start, train_score, cv_score))elaspe: 0.438091; train_score: 1.000000; cv_score: 0.982456
logistic_regression = model.named_steps['logistic_regression']
print('model parameters shape: {0}; count of non-zero element: {1}'.format(
logistic_regression.coef_.shape, #logistic_regression.coef_中保存的就是模型参数
np.count_nonzero(logistic_regression.coef_)))model parameters shape: (1, 495); count of non-zero element: 94
原来是特征30个,增加二阶多项式特征后,特征增加到495个,但l1正则后保留特征(非0)只有94。
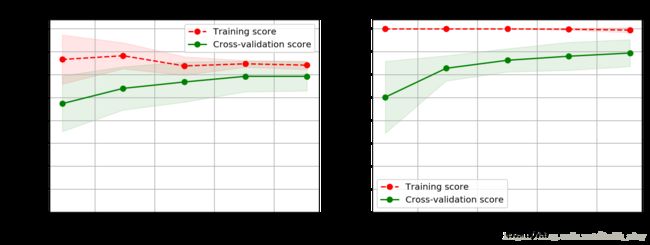
from common.utils import plot_learning_curve #调用库的画图方法
from sklearn.model_selection import ShuffleSplit
cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
title = 'Learning Curves (degree={0}, penalty={1})'
degrees = [1, 2]
penalty = 'l1'
start = time.clock()
plt.figure(figsize=(12, 4), dpi=144)
for i in range(len(degrees)):
plt.subplot(1, len(degrees), i + 1)
plot_learning_curve( plt,polynomial_model(degree=degrees[i], penalty=penalty),
title.format(degrees[i], penalty), X, y, ylim=(0.8, 1.01), cv=cv)
print('elaspe: {0:.6f}'.format(time.clock()-start))elaspe: 14.420778
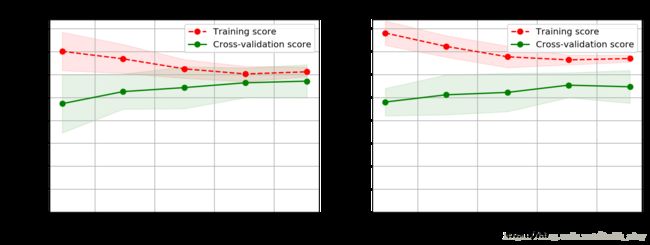
penalty = 'l2'
start = time.clock()
plt.figure(figsize=(12, 4), dpi=144)
for i in range(len(degrees)):
plt.subplot(1, len(degrees), i + 1)
plot_learning_curve(plt, polynomial_model(degree=degrees[i], penalty=penalty, solver='lbfgs'),
title.format(degrees[i], penalty), X, y, ylim=(0.8, 1.01), cv=cv)
print('elaspe: {0:.6f}'.format(time.clock()-start))elaspe: 3.629221
二阶L1正则模型最优,训练样本上评分最高,交叉验证样本评分也最高。但间隙比较大,可以采集更多训练数据