马走棋盘算法

这篇文章提到了一个马走棋盘的算法，大意如下：国际象棋中，马（Knight）走日（和中国象棋一样），能否实现这样一个算法，指定起点和终点，找到一条马行走的最短路线？

作者讲的很简单，只提到了用广度优先搜索（BFS），具体算法没有给出，我来了兴趣，想用C++完成它。既然要找到最短路径，BFS是一定的。继续往深处想，会碰到如下问题：1. 怎样保存路径？2. 怎样保证不走重复的格子？

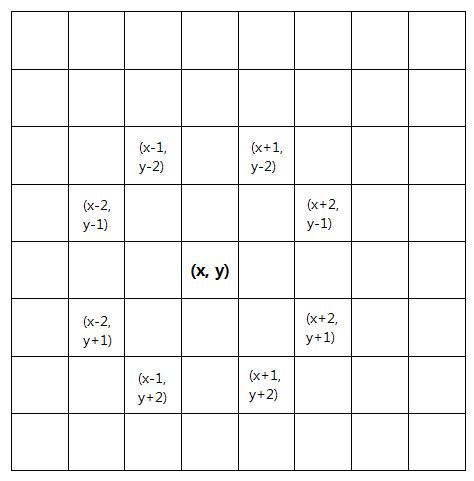
首先看行走的路线。如下图所示，若当前处在(x, y)，那下一步就可落在周围的8个格子里。普通的BFS是这样的：先将当前位置(x, y)存入队列，然后计算出下一步可到达的8个格子（即邻接表），(x+1, y-2)、(x+2, y-1)……等等，也存入队列，同时将(x, y)移出队列，然后重复这一过程。但这里有一个问题，(x, y)和(x+1, y-2)是互为邻接的，如此一来马在可能会在这两个位置跳来跳去，影响了下一层的搜索，因此需要记录已走过的格子。

我借助了一个数组，即把N*N的格子展开，变成一个元素个数为N*N的一维数组，每个元素的下标可与格子的位置进行转换index = N * col + row。走过了一个格子，就改变这个数组对应的值。比如在一个8*8的棋盘上，当前位置(x, y)=(3, 4)，下一步能走到(4, 2)，就标识一下array[4*8+2]即array[34]的值，表示已走过，之后不再走了，这样可保证不走重复的格子。

那么，刚刚还有问题，怎样保存路径？同样利用这个array。array的值不存别的，就存上一步的下标，比如(3, 4)能走到(4, 2)，则使array[4*8+2]=3*8+4，即array[34]=28；而(4,2)还能走到(5, 0)，再使array[40]=34，以此类推。最后发现已经到达了终点(m, n)，array[m*8+n]的值就是倒数第二步的下标，以此逆序找到路线。

当然，我们需要的是顺序的路线，最后可以使用一个stack，利用先进后出的特性顺序打印出路线。下面是代码实现的是在8*8的棋盘上，从(3, 4)到棋盘右下角(7, 7)的算法。

#include 
#include 
#include 

using namespace std;

#define N 8

struct Position
{
	int x;
	int y;
};

int PositionToIndex(const Position& pos)
{
	return pos.x * N + pos.y;
}

Position IndexToPosition(int index)
{
	Position pos = { index / N, index % N };
	return pos;
}

bool IsValid(const Position& pos)
{
	return (pos.x >= 0 && pos.x < N && pos.y >= 0 && pos.y < N);
}

int main(int argc, char* argv[])
{
	// 将棋盘延展成一维数组，序号表示当前格子，对应的值表示上一步的格子序号
	int* array = new int[N*N];
	for (int i = 0; i < N*N; i++)
	{
		array[i] = -1;
	}

	// 指定起始和结束位置
	Position start, end;
	start.x = 3;
	start.y = 4;
	end.x = N - 1;
	end.y = N - 1;

	bool finished = false;

	// 用栈存储每一步的序列位置，之后可反转输出
	stack finishSteps;

	// 利用队列实现广度优先搜索
	queue steps;
	steps.push(start);

	// 由于是第一步，约定值为-2，表示没有上一步
	array[PositionToIndex(start)] = -2;

	// 队列里的数据存储当前能走到的格子，若已为空表示已走完所有的格式，或所能走完的格子
	while (!steps.empty())
	{
		// 取出当前的格子，计算下一步，并将当前格子移出队列
		Position curPos = steps.front();
		int curIndex = PositionToIndex(curPos);
		steps.pop();

		// 已走到指定终点
		if (curPos.x == end.x && curPos.y == end.y)
		{
			finishSteps.push(PositionToIndex(end));	// 当前一步入栈
			int lastStep = curIndex;

			while (true)
			{
				// 一直找上一步，找到起始点为止
				lastStep = array[lastStep];
				if (lastStep == -2)
				{
					finished = true;
					break;
				}
				else
				{
					finishSteps.push(lastStep);
				}
			}
			break;
		}

		// 下一步有8个可走的情况，超出边界，或已探索到的忽略
		Position pos1 = { curPos.x + 1, curPos.y - 2 };
		if (IsValid(pos1))
		{
			int index1 = PositionToIndex(pos1);
			if (array[index1] == -1)
			{
				steps.push(pos1);
				array[index1] = curIndex;
			}
		}

		Position pos2 = { curPos.x + 2, curPos.y - 1 };
		if (IsValid(pos2))
		{
			int index2 = PositionToIndex(pos2);
			if (array[index2] == -1)
			{
				steps.push(pos2);
				array[index2] = curIndex;
			}
		}

		Position pos3 = { curPos.x + 2, curPos.y + 1 };
		if (IsValid(pos3))
		{
			int index3 = PositionToIndex(pos3);
			if (array[index3] == -1)
			{
				steps.push(pos3);
				array[index3] = curIndex;
			}
		}

		Position pos4 = { curPos.x + 1, curPos.y - 2 };
		if (IsValid(pos4))
		{
			int index4 = PositionToIndex(pos4);
			if (array[index4] == -1)
			{
				steps.push(pos4);
				array[index4] = curIndex;
			}
		}

		Position pos5 = { curPos.x - 1, curPos.y + 2 };
		if (IsValid(pos5))
		{
			int index5 = PositionToIndex(pos5);
			if (array[index5] == -1)
			{
				steps.push(pos5);
				array[index5] = curIndex;
			}
		}

		Position pos6 = { curPos.x - 2, curPos.y + 1 };
		if (IsValid(pos6))
		{
			int index6 = PositionToIndex(pos6);
			if (array[index6] == -1)
			{
				steps.push(pos6);
				array[index6] = curIndex;
			}
		}

		Position pos7 = { curPos.x - 2, curPos.y - 1 };
		if (IsValid(pos7))
		{
			int index7 = PositionToIndex(pos7);
			if (array[index7] == -1)
			{
				steps.push(pos7);
				array[index7] = curIndex;
			}
		}

		Position pos8 = { curPos.x - 1, curPos.y - 2 };
		if (IsValid(pos8))
		{
			int index8 = PositionToIndex(pos8);
			if (array[index8] == -1)
			{
				steps.push(pos8);
				array[index8] = curIndex;
			}
		}
	}

	// 完成，打印
	if (finished)
	{
		while (!finishSteps.empty())
		{
			Position pos = IndexToPosition(finishSteps.top());
			cout << "(" << pos.x << ", " << pos.y << "), ";
			finishSteps.pop();
		}
		cout << endl;
	}

	delete[] array;
	system("pause");

	return 0;
}