用R进行一元线性回归分析建模

概念：一元线性回归预测是指成对的两个变量数据的散点图呈现出直线趋势时，采用最小二乘法，找到两者之间的经验公式，即一元线性回归预测模型。根据自变量的变化，来估计因变量变化的预测方法。

我用的是R内置数据集mtcars，要预测的是当每加仑汽油能跑23英里（mpg=23）的车有多重（wt?）。下面贴一下代码，代码较简单，但重要的是这个流程！

1.

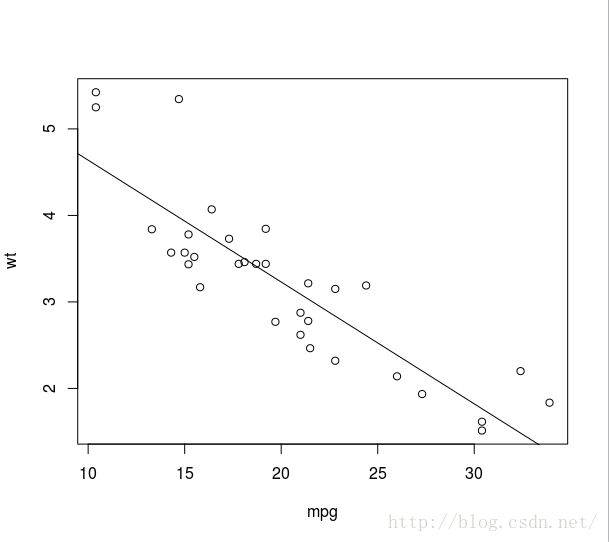
attach(mtcars);plot(mpg,wt);fm<-lm(wt~mpg)
summary(fm)
abline(fm)#加拟合曲线
coef(fm)#查截距与斜率（经济：回归系数）
resid(fm)#查残差

图是这样的

再看下这四张图

par(mfrow=c(2,2));plot(fm)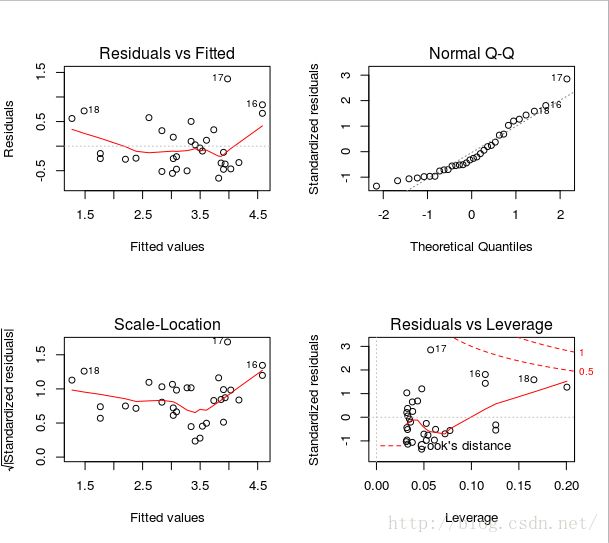

依次是预测残差图（查看是否线性），QQ正态检验图（查看正态性。应近似为45度直线），位置尺度诊断图（查看同方差性。水平线周围应随机分布），Cook距离/残差与杠杆图（查看离群点，高杠杆点）

2.检验模型

先对斜率/回归系数检验

n<-length(mpg);res<-resid(fm);b<-coef(fm)[2];s<-sqrt(sum(res^2)/(n-2))
SE<-s/sqrt(sum((mpg-mean(mpg))^2));t<-(b-(-1))/SE;pt(t,n-2,lower.tail = FALSE)

结果是9.763059e-33，远小于0.05，反对原假设，支持备择假设，所以斜率不是-1。但我总感觉哪不对= =

再对截距检验

bo<-coef(fm)[1];SEbo<-s*sqrt(sum(mpg^2)/(n*sum((mpg-mean(mpg))^2)));t<-(bo-7)/SEbo;pt(t,n-2)

结果是0.002165899，也小于0.05，同上

3.预测

predict(fm,data.frame(mpg=23))

结果是2.80743t

还可以看一下该模型95%的置信区间（95%置信区间就是说某个统计量落在这个区间里的可能性是95%）

sx<-sort(mpg);pred<-predict(fm,data.frame(mpg=sx),interval = 'confidence');pred

        fit       lwr      upr
1  4.582291 4.2403494 4.924232
2  4.582291 4.2403494 4.924232
3  4.173791 3.9024329 4.445149

fit是拟合值也可以单独看fitted(fm)，lwr是置信区间下限，upr是置信区间上限，下面画出来看一下

par(mfrow=c(1,1));plot(mpg,wt);abline(fm);lines(sx,pred[,2],lty=3);lines(sx,pred[,3],lty=3)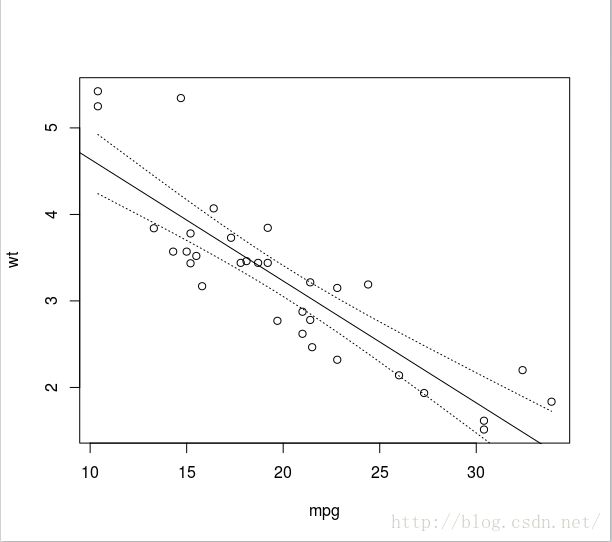

我感觉模型是没有问题的，但这数据不适合用一元线性回归模型。
最后别忘了解绑！

detach(mtcars)