1.学习总结(2分)
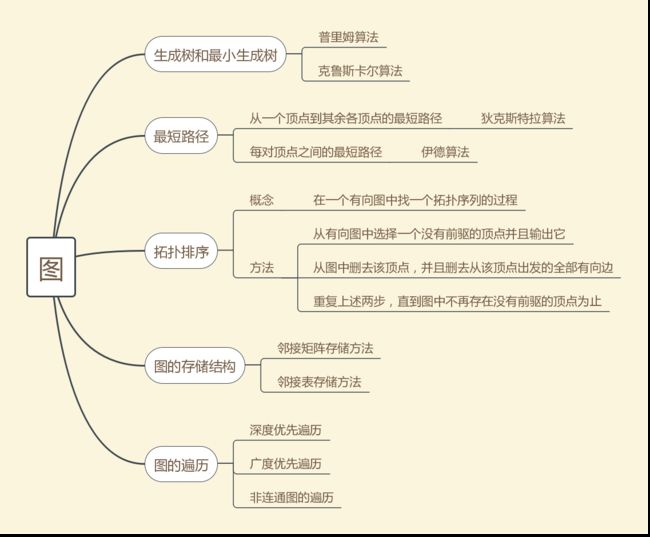
1.1图的思维导图
1.2 图结构学习体会
深度遍历算法:从某个初始顶点出发,首先访问初始顶点,选择一个与顶点相邻但没被访问过的顶点,再从该顶点出发进行深度优先遍历,直到所有顶点均被访问过为止。该遍历方法是个递归过程,每个顶点至多调用一次,其递归调用总次数为n。
广度遍历算法:首先访问初始顶点,接着访问初始顶点的所有未被访问过的邻接点,然后再按照邻接点的次序,访问每一个顶点的所有未被访问过的邻接点,以此类推,直至所有和初始顶点有路径相通的顶点都被访问为止。
Prim和Kruscal算法:都通过建立数组来记录带权值的边,Prim算法需要遍历lowcost数组找出最小边的邻接点,而Kruscal则需要设置一个辅助数组vset来判断两个顶点之间是否连通。
Dijkstra算法:用邻接矩阵存储,用s,u,dist,path数组分别表示最短路径,未选择顶点,源点到顶点目前的最短路径长度,最短路径长度。
拓扑排序算法:有向无环图中,选择一个没有前驱的顶点并输出它,从图中删去该顶点,并且删去从该顶点出发的全部有向边,重复上述步骤,直至图中不再存在没有前驱的顶点为止。
2.PTA实验作业(4分)
题目1:7-2 排座位
设计思路:如果两位宾客之间是朋友,且没有敌对关系,输出No problem;如果两位宾客之间不是朋友,但也不敌对,输出OK;如果两位宾客之间是敌对关系,并且有共同的朋友,则输出OK but...;如果两位宾客之间是敌对关系,并且没有共同的朋友,输出No way。
代码截图:
PTA提交列表说明
最开始关系分类不是很清楚,后面经过重新审题才明白了所有关系分类
题目2:7-3 六度空间
设计思路:此题为最短路径问题,采用最小生成树解决
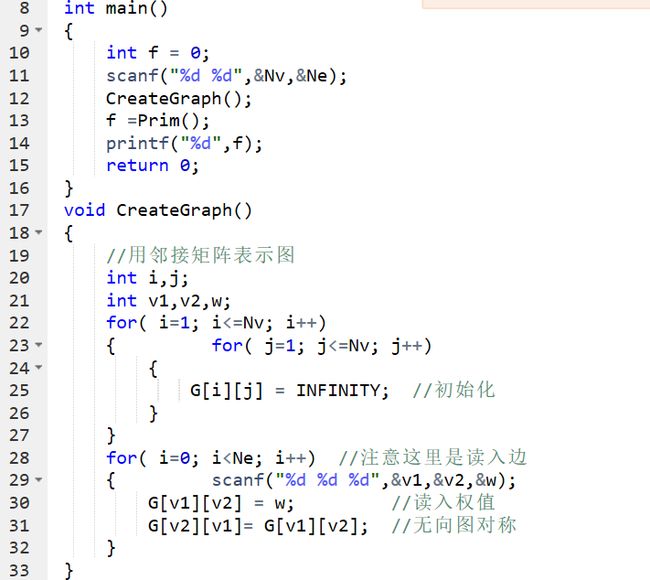
代码截图
PTA提交列表说明
对最小生成树算法还不够熟练,最后借助书本和百度完成此题
题目3:7-4 公路村村通
设计思路:最短路径问题,n个村庄可修n-1条路,用kruskal算法找最小生成树
代码截图
PTA提交列表说明
最开始用邻接矩阵表示图时没有输入正确
3.截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
3.1 PTA排名(截图带自己名字的排名)
3.2 我的总分:220
4. 阅读代码(必做,1分)
[cpp] view plain copy
#include
#include
#define MAXVEX 100 //最大顶点数
#define INFINITY 65535 //用65535来代表无穷大
int visited[MAXVEX]={0};
typedef struct
{
char vexs[MAXVEX]; //顶点表
int arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作边
int numVertexes, numEdges; //图中当前的顶点数和边数
}Graph;
void CreateGraph(Graph *g)
{ int i,j,k,w,t;
printf("输入顶点数,边数和t(中间用空格):");
scanf("%d %d %d", &(g->numVertexes), &(g->numEdges),&t);
printf("\n");
for(i=1;i<=g->numVertexes;i++)
{
getchar();
printf("输入第%d顶点信息vexs[%d]=",i,i);
scanf("%c",&(g->vexs[i]));
}
printf("\n");
for(i=1;i<=g->numVertexes;i++)
for(j=1;j<=g->numVertexes;j++)
if (t>2) g->arc[i][j] = INFINITY;
else g->arc[i][j]=0;
for(k=1;k<=g->numEdges;k++)
{
printf("输入i j(中间用空格):");
scanf("%d %d",&i,&j);
if(i>g->numVertexes ||j>g->numVertexes) exit(0);
if(t>2)
{
printf("输入w:");
scanf("%d",&w);
g->arc[i][j]=w;
if(t==3) g->arc[j][i]=w;
}
else
{ g->arc[i][j]=1;
if (t==1) g->arc[j][i]=1;
}
}
printf("\n");
printf("输出邻接矩阵:\n");
for(i=1;i<=g->numVertexes ;i++)
{
for(j=1;j<=g->numVertexes ;j++)
{
printf("%8d",g->arc[i][j]);
if(t>2&&g->arc[i][j]==65535)
g->arc[i][j]=0;
else if(t>2&&g->arc[i][j]!=65535)
g->arc[i][j]=1;
}
printf("\n");
}
}
void dfs (Graph g,int i) //广度优先搜索,从顶点i开始遍历
{
int j;
printf("%d->",i); //输出访问顶点
visited[i]=1; //全局数组访问标记置1表示已经访问
for(j=1; j<=g.numVertexes; j++)
if ((g.arc[i][j]==1)&&(!visited[j]))
dfs (g,j);
}
void bfs (Graph g,int i)
{
int visited[MAXVEX]={0};
int q[g.numVertexes+1] ;
int f,r,j ;
f=r=0 ;
printf("%d->",i);
visited[i]=1 ;
r++;
q[r]=i ;
while (f
for (j=1; j<=g.numVertexes; j++)
if ((g.arc[i][j]==1)&&(!visited[j]))
{ printf("%d->",j); ; visited[j]=1 ; r++; q[r]=j ; }
}
}
int main()
{
Graph g;
int i;
printf("t为1~4,分别表示无向图、有向图、带权无向图、带权有向图\n");
CreateGraph(&g);
printf("\n输入i:");
scanf("%d",&i);
printf("\n深度优先搜索遍历:");
dfs (g,i);
printf("NULL\n");
printf("广度优先搜索遍历:");
bfs (g,i);
printf("NULL\n");
return 0;
}