git地址:https://github.com/705393356/operation
组员:洪崇伟、林浩
一、PSP表-预估耗时
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 60 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 60 | 30 |
| Development | 开发 | 470 | 505 |
| · Analysis | · 需求分析 (包括学习新技术) | 30 | 20 |
| · Design Spec | · 生成设计文档 | 10 | 15 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 15 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 20 | 10 |
| · Design | · 具体设计 | 30 | 25 |
| · Coding | · 具体编码 | 300 | 320 |
| · Code Review | · 代码复审 | 10 | 20 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 80 |
| Reporting | 报告 | 30 | 40 |
| · Test Report | · 测试报告 | 10 | 10 |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 10 | 20 |
| 合计 | 560 | 575 |
二、解题思路
- 首先这个题目有分数的要求,所以在一开始就应该考虑到分数的实现,因为java不存在可以处理分数运算的类,这个应该在一开始就考虑清楚,我们的处理方式是将整数与分数作为一个对象来处理,即整数就是分母为1的分数。
- 计算便可以直接用分数的运算了。
- 因为题目要求命令行,所以我们找了脚本的方法来实现命令行操作
三、设计实现过程
- 有三个包,分别为service(服务包),model(实体包),main(主程序)
- service里有四个类,分别包括了计算操作,分数实体类处理操作,检查操作与生成式子操作
- model里有三个类,计算等式的计算类,分数类,结果集合
- main里主要是以上两个包中的方法对应整合
四、代码说明
整个程序难点就在于分数的运算,整数,小数运算可以用自带的操作运算符,但是在java里面却没有一个基本类型去表示分数。很多人可能会考虑到把分数化成小数再运算再转为分数,其实不然,有很多情况下是无法进行转换的,因为java语言中的double类型所表示的精度也是有限的。于是结合java面向对象的思想特征,应该先定义要给分数类,并封装相关的运算方法。代码如下
分数类:
/*
* 构建一个分数类,用来表示分数,封装相关的方法
*/
public class Fraction {
private int denominator;// 分母
private int nominator;// 分子
// 构建一个分数
public Fraction(int denominator, int nominator) {
super();
this.denominator = denominator;
this.nominator = nominator;
}
public Fraction(int nominator) {
this.denominator = 1;
this.nominator = nominator;
}
public Fraction() {
super();
}
// 判断构建的是一个分数还是一个整数,不超过limit的数值
public Fraction(boolean l, int limit) {
Random r = new Random();
// 这是一个分数
if (l == true) {
int index = r.nextInt(limit);
int index2 = r.nextInt(limit);
while(index==0) {
index = r.nextInt(limit);
// System.out.println("会生成0:"+index);
}
// System.out.println("不会生成0:"+index);
this.denominator = index;
this.nominator = index2;
// 这是一个整数
} else {
int index = r.nextInt(limit);
this.denominator = 1;
this.nominator = index;
}
}
public int getDenominator() {
return denominator;
}
public void setDenominator(int denominator) {
this.denominator = denominator;
}
public int getNominator() {
return nominator;
}
public void setNominator(int nominator) {
this.nominator = nominator;
}
// 加法运算
public Fraction add(Fraction r) {
int a = r.getNominator();// 获得分子
int b = r.getDenominator();// 获得分母
int newNominator = nominator * b + denominator * a;
int newDenominator = denominator * b;
Fraction result = new Fraction(newDenominator, newNominator);
return result;
}
// 减法运算
public Fraction sub(Fraction r) {
int a = r.getNominator();// 获得分子
int b = r.getDenominator();// 获得分母
int newNominator = nominator * b - denominator * a;
int newDenominator = denominator * b;
Fraction result = new Fraction(newDenominator, newNominator);
return result;
}
// 分数的乘法运算
public Fraction muti(Fraction r) { // 乘法运算
int a = r.getNominator();// 获得分子
int b = r.getDenominator();// 获得分母
int newNominator = nominator * a;
int newDenominator = denominator * b;
Fraction result = new Fraction(newDenominator, newNominator);
return result;
}
// 分数除法运算
public Fraction div(Fraction r) {
int a = r.getNominator();// 获得分子
int b = r.getDenominator();// 获得分母
int newNominator = nominator * b;
int newDenominator = denominator * a;
Fraction result = new Fraction(newDenominator, newNominator);
return result;
}
// 用辗转相除法求最大公约数
private static long gcd(long a, long b) {
return b == 0 ? a : gcd(b, a % b);
}
// 对分数进行约分
public void Appointment() {
if (nominator == 0 || denominator == 1)
return;
// 如果分子是0或分母是1就不用约分了
long gcd = gcd(nominator, denominator);
this.nominator /= gcd;
this.denominator /= gcd;
}
public int existZero(){
if(this.nominator<0||this.denominator<0){
return 0;
}else {
return 1;
}
}
}在这个分数类中,我们定义了分子和分母,然而整数其实一个分数,只不过这个分数的分母为1.
至于运算也只是根据运算法则对分数的分子分母进行运算,保证了
在程序中,运算符的出现数量以及类型是随机的,用数组进行存储,用一个随机数Ramdon
char[] c = { '+', '-', '*', '÷' }//显示四种基本运算符
r.nextInt(4);//随机生成四种基本运算符的一种
int s = r.nextInt(3);// 生成运算符的数量
用这种随机数的形式保证了式子的随机性。随机出现,随机生成,之后只要根据多项式的运算,对式子进行运算即可。之后将生成的式子放在一个list里面,包括运算符以及分数类
运算
四则运算具有优先级,先算乘除再算加减,如果采用if表达的形式,对优先级进行判定,那么三个运算符就有64种情况,很明显是不可采取的,容易使代码失去可读性,在这种情况下,我们采取递归来解决这种问题。
//分式的计算方法
public Fraction calculate(List l){
int muldiv = MulDivExist(l);
if(muldiv != -1){
String s = MulDiv(l,muldiv);
if(s.equals("error")){
return null;
}
}else {
String s = AddSub(l);
if(s.equals("error")){
return null;
}
}
if (l.size() == 1) {
return (Fraction) l.get(0);
}
return calculate(l);
}
/*
* 判断分式里面是否有乘除
* 有乘除返回乘除的位置,没乘除返回-1
*/
public int MulDivExist(List list){
for (int i = 0; i < list.size(); i++) {
if (list.get(i).equals("*") || list.get(i).equals("/")) {
return i;
}
}
return -1;
}
//计算分式的乘除,计算结果往前放
public String MulDiv(List l,int muldiv){
String fuhao = (String) l.remove(muldiv);
Fraction first = (Fraction) l.get(muldiv-1);
Fraction last = (Fraction) l.get(muldiv);
l.remove(muldiv);
if (fuhao.equals("*")) {
Fraction result = first.muti(last);
l.set(muldiv - 1,result);
if(result.existZero()==0){
return "error";
}
}
if (fuhao.equals("/")) {
Fraction result = first.div(last);
l.set(muldiv - 1,result);
if(result.existZero()==0){
return "error";
}
}
return "right";
}
//计算分式的加减,计算结果往前放
public String AddSub(List list){
for (int i = 0; i < list.size(); i++) {
if (list.get(i).equals("+")) {
Fraction first = (Fraction) list.get(i-1);
list.remove(i);
Fraction last = (Fraction) list.get(i);
list.remove(i);
Fraction result = first.add(last);
list.set(i - 1, result);
i--;
if(result.existZero()==0){
return "error";
}
}
if (list.get(i).equals("-")) {
Fraction first = (Fraction) list.get(i-1);
list.remove(i);
Fraction last = (Fraction) list.get(i);
list.remove(i);
Fraction result = first.sub(last);
list.set(i - 1, result);
i--;
if(result.existZero()==0){
return "error";
}
}
}
return "right";
}
在递归计算之前,先做一个判定,对生成的式子进行判别,如果有乘除,那就优先采用乘除的递归,然后再用递归计算加减。这样就保证了运算的优先级问题。
去重
式子需要去重,保证每次生成的都是不一样的式子。去重采用了一种字符串比较的方法,在此之前,重写了分数类的toString方法,只要两个字符串组成字符完全相同即:组成两个式子的字符完全一样就可以说明这两个式子是重复的。
重写的toString方法
@Override
public String toString() {
Appointment();
if(this.denominator == 0){
System.out.println(this.nominator + "|" + this.denominator);
System.out.println("分母为0");
}
if (this.denominator == 1 || this.nominator == 0) {
return "" + this.nominator;
}else if (this.nominator > this.denominator) {
if(nominator % denominator==0){
return "" + nominator / denominator;
}
return "" + nominator / denominator + "," + nominator % denominator + "/" + denominator;
}else{
return "" + this.nominator + "/" + this.denominator;
}
}
去重代码:
//查重,若有重复那就返回ture
public boolean isRepeat(List> list, List set) {
if (list.size() <= 0) {
return false;
}
Iterator iterator = set.iterator();
for (List l_set : list) {
if (l_set == null || l_set.size() != set.size() || l_set.size() <= 0 || set.size() <= 0) {
continue;
}
int i = 0;
while(iterator.hasNext()){
if(l_set.contains(iterator.next())){
i = i+1;
}
}
if(i == set.size()){
return true;
}
}
return false;
} 通过这段去重代码可以将重复的式子筛选出去,保证了整个文件中式子的独立性。
计算结果的校验
一个式子,等式右边的就是结果,一个式子就是一个字符串,只要用字符串处理函数将等式右边的结果截取出来,与用户的输入进行对比就能得出结果与否。
相关代码如下:
while((str1=reader1.readLine())!=null&&(str2=reader2.readLine())!=null){
if(!str1.trim().equals(str2.trim())){
String[] str = str1.split("\\.");
error = error + str[0]+ ",";
errornum ++ ;
}else {
String[] str = str1.split("\\.");
correct = correct + str[0] + ",";
correctnum ++;
}
}
if(error.equals("")){
error = "Wrong: " + errornum + "";
}else {
error = "Wrong: " + errornum + "(" + error.substring(0,error.length()-1) + ")";
}
if(correct.equals("")){
correct = "Correct: " + correctnum + "";
}else {
correct = "Correct: " + correctnum + "("+correct.substring(0, correct.length()-1)+")";
}
m.put("wrong", error);
m.put("correct", correct);
return m;
}
将结果放在一个map中,便于读取,得出结果。
五、测试运行
首先要将jar文件与bat文件放置在同一目录下
进入命令行界面
若是未输入参数,则
正确输入生成题目的参数命令
正确输入测试文件与答案文件
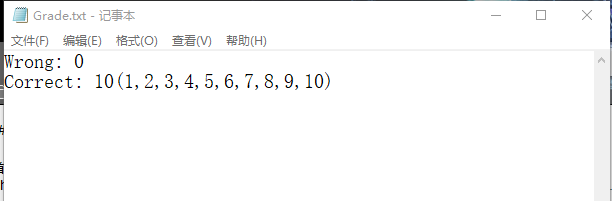
若是全对
出现错误
六、总结
问题
- 一开始并没有思考清楚题目中的分数问题,想着解决了分数就行,结果最后推倒重来。
- 在程序开发过程中,虽然使用了git管理,但因为不熟悉发生了一些错误,修改的代码上传后下拉发生了冲突,以后在团队编程中,要注意代码改动情况,和队员对接好。
结对好处
- 可以互相发现对方的编码问题,及时做出调整
- 在讨论中,不断地想出新的点子来实现功能,很好的促进项目的开发