后缀数组(SuffixArray) 学习笔记
后缀数组
前面有介绍过后缀树,后缀树对于我们针对某些字符串的处理使得如鱼得水,美中不足的是后缀树的代码实现复杂,只能让很多人望而却步。这次我们来介绍后缀树组:一个处理字符串的有力工具,也是一个后缀树的精美替代品,同样可以方便解决很多字符串问题。它比后缀树更加容易实现编码,也可以在不损失效率的情况下实现很多后缀树的功能,占用内存也比后缀树小很多,尤其是在模式匹配数据规模庞大的操作中实用性很高,很多搜索引擎也都在使用这样一个神奇的数据结构。
先来看看几个概念:
1> 假设有一个字符串:S 针对字符串S, Len(s) 表示字符串对应的长度
2>后缀Suffix(i): 对于字符串中的任意一个索引i开始到字符串结束的子串称之为该字符串S的一个后缀。比如suffix(i) = S[i...len(s)].
3>后缀数组SA(i):将一个字符串S的所有后缀串,按照字典顺序依次放入到一个数组中,这个数组表明了S的所有后缀串的字典顺序,这样一个有序的后缀串数组就是后缀数组。后缀数组SA(i)表示排名第i的字符串是谁?当然要注意的是这里的SA(i)的值是一个索引,是第i名的后缀串在原有串的起始索引值。
4>名次数组Rank(i): 名次数组是保存的是suffix(i)这个后缀在所有后缀串中的排名。不难发现名次数组和后缀数组是个互逆的排名。SA数组是表示排第几的是谁,而Rank则表示的是谁排第几。也就是说SA[Rank[i]] = i,从而也就是说在知道任意一个数组的情况下O(n)时间复杂度内快速求得另外一个数组。有了名次数组我们也可以在O(1)时间内求出任意两个后缀的大小关系。
如何构造后缀数组:
1> 将字符串S的所有后缀当成独立的字符串进行常规排序,平方级O(n^2)时间复杂度,因为忽略了所有后缀串之间的相互联系,将所有后缀当成独立的字符串进行排序从而构造效率低下,当然你对时间要求没那么高,数据规模没那么大当然可以轻松实现。这也不是本文的重点。
2> 根据罗穗骞的论文我们可以使用倍增算法(Doubling Algorithm),可以再O(nlogn)时间内构造出后缀数组,编码简单易行。
3> 罗穗骞的论文还提供了一种更为高效的构造算法:DC3算法,这是一个优秀的线性算法O(N)时间复杂度内构造后缀数组,编码相对于DA算法复杂。
本文重点描述倍增算法(DA)构造后缀数组,提供的倍增算法来自于罗穗骞的论文所描述的算法,这里仅提供对该算法的一些个人梳理,论文和所有求证过程需要自己去拜读原始论文《后缀数组——处理字符串的有力工具》。
倍增算法(DA):设字符串长度为n, 为了方便比较大小,可以再字符串的后面添加一个字符,这个字符没有在前面的字符中出现过,而且比前面的字符都要小,通常这个补充字符是0或者$。倍增算法就是用倍增的方法对每个字符开始的长度为2^k的子串进行排序,求出排名rank值。从k=0开始, 每次k加1, 当2^k大于n以后,每个子串开始的长度为2^k的子串便相当于所有的后缀。而且这些子串已经比较出大小了,所有的rank都没有相同的值,这个rank就是最后的结果。每一次排序都利用上一次的2^(k-1)的字符串的rank值, 那么长度为2^k的字符串的rank就可以用两个长度为2^(k-1)的字符串的排名为关键字表示出来,对关键字进行计数排序,便可以得到长度为2^k的字符串的rank。
对于任意的字符串X和Y,我们都可以进行简单的长度为k前缀比较,从而进一步能到2k前缀的长度比较,最终变成为将得到倍增关系的前缀比较,从而到达所有后缀比较的目的。
把n个后缀按照k-前缀意义下的大小关系从小到大排序,将排序后的后缀的开头位置顺次放入数组SAk中,称为k-后缀数组。用Rankk[i]保存Suffix(i)在排序中的名次,称数组Rankk为k-名次数组。更进一步,利用SAk可以在O(n)时间内求出Rankk,利用Rankk可以在常数时间内对两个后缀进行k-前缀意义下和2k-前缀意义下的大小比较。也可以很方便地对所有的后缀在2k-前缀意义下排序,在O(n)时间内求出SA2k进一步推出Rank2k.
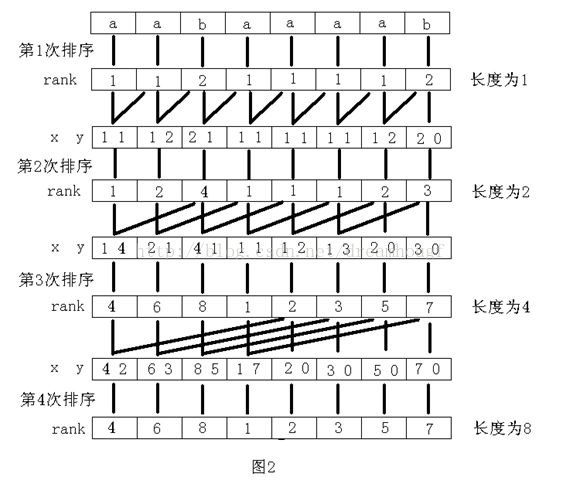
当m=2^k已经大于等于n(m>=n) 时,我们已经知道SAm=SA, Rankm=Rank,我们在O(nlogn)时间内构造出了后缀数组和名次数组。借用论文的一个例子图证一下倍增关系排序,以字符串“aabaaaab”为例,整个过程下图所示。其中x、y 是表示长度为2k 的字符串的两个关键字。
后缀树组倍增算法代码:
const int N = 1002;
// 由于末尾填了0,所以如果r[a]==r[b](实际是y[a]==y[b]),
// 说明待合并的两个长为j的字符串,前面那个一定不包含末尾0,
// 因而后面这个的起始位置至多在0的位置,不会再靠后了,因而不会产生数组越界。
int cmp(int *r,int a,int b,int l){
return (r[a]==r[b]) && (r[a+l]==r[b+l]);
}
int rank[N],height[N], sa[N];
int wa[N],wb[N],ws[N],wv[N];
/*
Da倍增算法实现
输入:字符串数组r,后缀数组SA初始化,长度n
m代表字符串中字符的取值范围,是基数排序的基数范围,字母可以直接取128
如果原序列本身都是整数的话,则m可以取比最大的整数大1的值。
输出:无
*/
void DA(char* r, int* sa, int n, int m)
{
int i, j, p, *x = wa, *y = wb, *t;
// 前四个for先对字符串首字符进行一次基数排序,得到排序后的SA
for (i = 0; i < m ; i++) ws[i] = 0;
for (i = 0; i < n; i++) ws[x[i] = r[i]]++;
for (i = 1; i < m; i++) ws[i] += ws[i-1];
for (i = n-1; i >= 0; i--) sa[--ws[x[i]]] = i;
// 下面for循环主要实现了倍增算法的内容,j从长度1开始一直递增
// 每次倍数增加,也是每次带合并的字符串的长度值。p是每次rank时
// 所不需要的数量,当p和n相同时说明已经排序结束了。m是基数排序
// 所需要的取值range。
for (j = 1, p = 1; p < n; j *= 2, m = p)
{
// 下面两个for是对第二个关键字进行排序
for (p = 0, i = n-j; i < n; i++) y[p++] = i; // 通过图2我们可以看到当长度为j时,n-j开始的后缀串都没有第二个关键字
//那么这些字符串的第二个关键字都是补齐的最小字符,按照第二关键字排序后
// 这些字符串都将排在最前面。
for (i = 0; i < n; i++) if (sa[i] >= j) // 这里将有第二关键字的后缀进行排序y[]里存放的是按第二关键字排序的字符串下标
y[p++] = sa[i] - j;
for (i = 0; i < n; i++) wv[i] = x[y[i]]; // 这里提取出每个字符串的第一关键字以便后续排序
// 下面四行便是对后缀的第一关键字进行基数排序
for (i = 0; i < m; i++) ws[i] = 0;
for (i = 0; i < n; i++) ws[wv[i]]++;
for (i = 1; i < m; i++) ws[i] += ws[i-1];
for (i = n-1; i >= 0; i--) sa[--ws[wv[i]]] = y[i];
// 下面就是计算合并之后的rank值了,用x[]存储计算出的各字符串rank的值
// 要注意的是但计算rank的时候必须让相同的字符串有相同的rank,要不然p==n之后就结束了。
for (t = x, x = y, y = t, p = 1, x[sa[0]] = 0, i = 1; i < n; i++)
{
x[sa[i]] = cmp(y, sa[i-1], sa[i], j)?p-1:p++;
}
}
}
确实光有后缀数组和名次数组还不能很好的解决问题,这里还要介绍后缀数组的辅助工具:
后缀数组的最佳搭档——LCP, 定义两个字符串的最长公共前缀(Longest Common Prefix) lcp(u,v)=max{i|u=iv} 也就是从头开始比较u和v的对应字符持续相等的最远值。
定义 LCP(i,j)=lcp(Suffix(SA[i]),Suffix(SA[j]))也就是SA数组中第i个和第j个后缀的最长公共前缀。对任何1≤i
height 数组:定义height[i]=suffix(sa[i-1])和suffix(sa[i])的最长公共前缀,也就是排名相邻的两个后缀的最长公共前缀, 即height[i]=LCP(i-1, i)。height数组是后缀数组处理字符串的核心,基本上所有的处理都要依赖height数组实现。
LCP(i,j)=min{height[k]| i+1≤k≤j} 计算LCP(i,j)等价于询问数组height中下标从i+1 到 j 范围内所有元素的最小值, 相当于再求区间最值问题,经典的RMQ问题!
根据lcp(Suffix(i),Suffix(j))=LCP(Rank[i],Rank[j]), 可以在常数时间内计算出任何两个后缀的最长公共前缀。那么如何高效的求出height 值:
如果按height[2],height[3],……,height[n]的顺序计算,最坏情况下时间复杂度为O(n2) 。这样做并没有利用字符串的性质。
定义 h[i]=height[rank[i]],也就是suffix(i)和在它前一名的后缀的最长公共前缀。
h 数组有以下性质:
h[i]≥h[i-1]-1
证明:
设suffix(k)是排在suffix(i-1)前一名的后缀,则它们的最长公共前缀是h[i-1]。那么suffix(k+1)将排在suffix(i)的前面(这里要求h[i-1]>1,如果h[i-1]≤1,原式显然成立)并且suffix(k+1)和suffix(i)的最长公共前缀是h[i-1]-1,所以suffix(i)和在它前一名的后缀的最长公共前缀至少是h[i-1]-1。按照h[1],h[2],……,h[n]的顺序计算,并利用h 数组的性质,时间复杂度可
以降为O(n)。实现的时候其实没有必要保存h 数组,只须按照h[1],h[2],……,h[n]的顺序计算即可:
void calHight(int* r, int* sa, int n)
{
int i, j, k = 0;
for (i = 1; i <= n; i++) rank[sa[i]] = i;
for (i = 0; i < n; height[rank[i++]] = k)
for (k?k--:0, j = sa[rank[i]-1]; r[i+k] == r[j+k]; k++);
}上述过程是我们针对倍增算法求后缀数组的方法,DC3算法我们在此不做讨论,只贴出实际的代码,有兴趣的同学可以直接去分析研究论文《后缀数组——处理字符串的有力工具》上述论证过程相关的过程和源码也均来自论文,特此说明!
DC3算法实现:
#define F(x) ((x)/3+((x)%3==1?0:tb))
#define G(x) ((x)=0;i--) b[--ws[wv[i]]]=a[i];
return;
} void dc3(int *r,int *sa,int n,int m)
{
int i,j,*rn=r+n,*san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
r[n]=r[n+1]=0;
for(i=0;i后缀数组能解决哪些问题呢:
1> 给定一个字符串,询问某两个后缀的最长公共前缀。
2>给定一个字符串,求最长重复子串,这两个子串可以重叠
3>给定一个字符串,求最长重复子串,这两个子串不能重叠
4>给定一个字符串,求至少出现k 次的最长重复子串,这k 个子串可以重叠
5>给定一个字符串,求不相同的子串的个数
6>给定一个字符串,求最长回文子串
7> 给定一个字符串L,已知这个字符串是由某个字符串S 重复R 次而得到的,求R 的最大值
8> 给定一个字符串,求重复次数最多的连续重复子
9> 给定两个字符串A 和B,求最长公共子串。
10>给定两个字符串A 和B,求长度不小于k 的公共子串的个数(可以相同)
11>给定n 个字符串,求出现在不小于k 个字符串中的最长子串。
12>给定n 个字符串,求在每个字符串中至少出现两次且不重叠的最长子串
13>给定n 个字符串,求出现或反转后出现在每个字符串中的最长子串。
上述问题均可在论文中得到解答,更多信息请自行翻阅罗穗骞的论文原稿《后缀数组——处理字符串的有力工具》