python实现霍夫曼树以及编码
python实现霍夫曼树以及编码
再看移动通信的时候了解到了霍夫曼(Huffman)编码,花了一些时间进行了霍夫曼编码的python实现。文章内容包括霍夫曼树的生成,以及相应编码的生成,每一部分都会有完整的代码,个人python3测试无误,可以放心大胆地Ctrl+C哈哈哈
(全部完整版拉到最后)
P1 节点的定义类
为节点定义名称,值,左右孩子,二进制编码数字
class Node(object):
def __init__(self,name=None,value=None):
self._name=name
self._value=value
self._left=None
self._right=None
self._codevalue='0'
P2 构建霍夫曼树
我们先来看一看霍夫曼树是如何构成的
如给定一组数:
char_weights=[('a',9),('b',12),('c',6),('d',3),('e',5),('f',15)]
如何形成霍夫曼树呢?
1.首先对这组数进行从大到小的排序
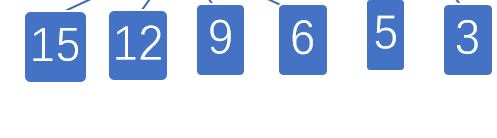
2.再将这些树作为叶节点,也就是二叉树的最底层,向上依次生成节点
那么,该如何生成呢?
每一次作为左右孩子生成父节点的是所有节点中权重最小的
当然,这里的节点是指所有没有父节点的节点,已经连接父节点的不算在内
新生成的父节点权重为两个子节点的权重值和
我们来根据最终生成霍夫曼树的图看一下(算法中使用的数据也是这个图,大家可以复制源代码debug一步一步看)
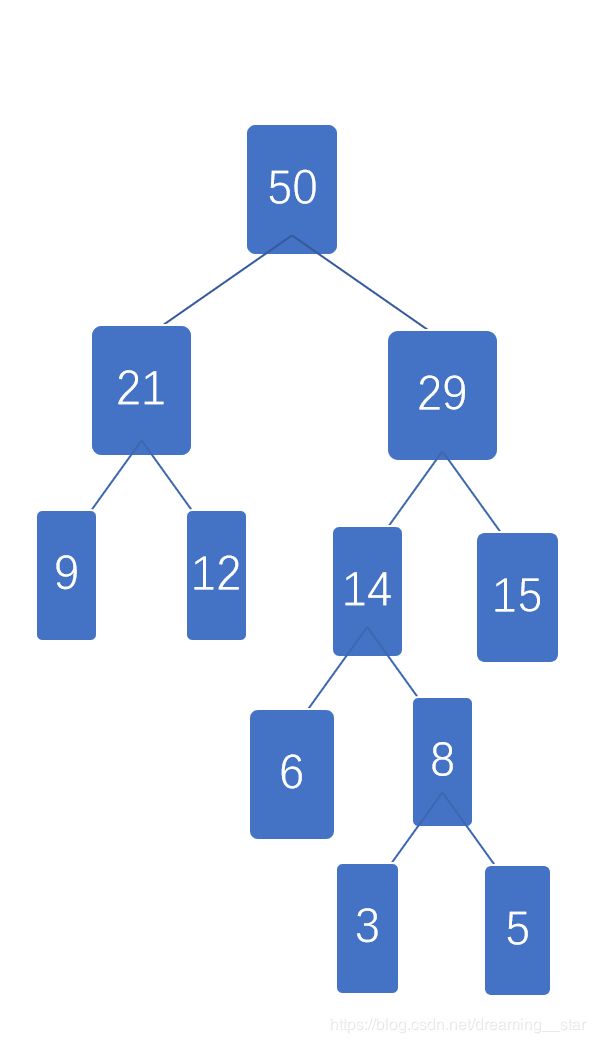
因为纯word手画,整不明白,就不画分步的了,扎心
接下来直接看代码吧,如何实现霍夫曼树
#哈夫曼树类
class HuffmanTree(object):
#根据Huffman树的思想:以叶子节点为基础,反向建立Huffman树
def __init__(self,char_weights):
self.codeway = {}#存储节点对应的编码数,1or0
self.a=[Node(part[0],part[1]) for part in char_weights] #根据输入的字符及其频数生成叶子节点
while len(self.a)!=1:#如果没有到达根节点
self.a.sort(key=lambda node:node._value,reverse=True)#根据节点的value进行从大到小的排序
c=Node(value=(self.a[-1]._value+self.a[-2]._value))#对于权值最小的两个节点加和作为新节点c的value
c._left=self.a.pop(-1)#把排序完的树叶节点挂靠在c上,作为左右节点
c._right=self.a.pop(-1)
self.a.append(c)#bac作为节点连在树上
self.root=self.a[0]
P3 实现霍夫曼编码
写了两种方法,大同小异吧,看你们习惯用哪种
第一种
这个是根据大佬的c语言代码改的,用的时候一定要注意列表的大小,不然会报错
def pre(self, tree, length,l):
if l==0:
self.b=[0]*length
node = tree
if (not node):
return
elif node._name:
print(node._name + '的编码为:',end=' ')
for i in range(l):
print(self.b[i],end=' ')
print('\n')
return
这个是写在霍夫曼树生成类里面的,下面是调用代码
char_weights=[('a',9),('b',12),('c',6),('d',3),('e',5),('f',15)]
tree=HuffmanTree(char_weights)
tree.pre(tree.root,length,0)#length定义在文章结尾完整代码的main函数里
返回结果如下:
a的编码为: 0 0
b的编码为: 0 1
c的编码为: 1 0 0
d的编码为: 1 0 1 0
e的编码为: 1 0 1 1
f的编码为: 1 1
第二种
# 函数得到每一个叶结点的路径
def binaryTreePaths(self, root):
if not root:#如果root不存在
return []
if not root._left and not root._right:#如果root就是一个叶节点
return [str(root._value)]
pathList = []#用来存储路径
if root._left:#沿左子树下行递归遍历直到到达了叶节点
root._left._codevalue = '0'
pathList+=self.binaryTreePaths(root._left)
self.codeway[root._left._value]=root._left._codevalue
if root._right:
root._right._codevalue='1'
pathList+=self.binaryTreePaths(root._right)
self.codeway[root._right._value] = root._right._codevalue
for index, path in enumerate(pathList):#枚举pathList,得到对应节点路径的存放路径
pathList[index]=str(root._value) + ' ' + path
return pathList
#如果上一个函数返回两个值,然后用result[0]取用pathList的话会出现
#把12看成两个数1,2的情况,我暂时没有想出来为什么,希望大佬们指点指点
#所以我又写了一个函数专门返回codeway
def code_way(self):
return self.codeway
下面是调用方法
char_weights=[('a',9),('b',12),('c',6),('d',3),('e',5),('f',15)]
tree=HuffmanTree(char_weights)
length=len(char_weights)
pathList = tree.binaryTreePaths(tree.root)
codeway=tree.code_way()
print(codeway)
print("路径输出为: ",pathList)
for i in pathList:
i=i.split(' ')[1:]#根节点不参与编码,所以切掉
print("数字 ",i[-1],"的编码是:",end='')
for j in i:
print(codeway[int(j)],end='')
print('\n')
返回结果如下:
{9: '0', 12: '1', 21: '0', 6: '0', 3: '0', 5: '1', 8: '1', 14: '0', 15: '1', 29: '1'}
路径输出为: ['50 21 9', '50 21 12', '50 29 14 6', '50 29 14 8 3', '50 29 14 8 5', '50 29 15']
数字 9 的编码是:00
数字 12 的编码是:01
数字 6 的编码是:100
数字 3 的编码是:1010
数字 5 的编码是:1011
数字 15 的编码是:11
a的编码为: 0 0
b的编码为: 0 1
c的编码为: 1 0 0
d的编码为: 1 0 1 0
e的编码为: 1 0 1 1
f的编码为: 1 1
欢迎交流!
全部完整代码
(上面的代码每一部分都没有问题,用头担保是可以跑出来滴。方便大家粘贴下面是完整版。但是希望大家可以不要简单的复制代码,也帮我提出一些解决方案呀,么么哒)
#节点类,当树中叶节点最大数为n时,霍夫曼树的总节点数为2n-1
class Node(object):
def __init__(self,name=None,value=None):
self._name=name
self._value=value
self._left=None
self._right=None
self._codevalue='0'
#哈夫曼树类
class HuffmanTree(object):
#根据Huffman树的思想:以叶子节点为基础,反向建立Huffman树
def __init__(self,char_weights):
self.codeway = {}#存储节点对应的编码数,1or0
self.a=[Node(part[0],part[1]) for part in char_weights] #根据输入的字符及其频数生成叶子节点
while len(self.a)!=1:#如果没有到达根节点
self.a.sort(key=lambda node:node._value,reverse=True)#根据节点的value进行从大到小的排序
c=Node(value=(self.a[-1]._value+self.a[-2]._value))#对于权值最小的两个节点加和作为新节点c的value
c._left=self.a.pop(-1)#把排序完的树叶节点挂靠在c上,作为左右节点
c._right=self.a.pop(-1)
self.a.append(c)#bac作为节点连在树上
self.root=self.a[0]
#方法一
def pre(self, tree, length,l):
if l==0:
self.b=[0]*length
node = tree
if (not node):
return
elif node._name:
print(node._name + '的编码为:',end=' ')
for i in range(l):
print(self.b[i],end=' ')
print('\n')
return
#是树的左子节点的话赋值为0,直到到达叶结点之后print了编码,再对考虑右子树
self.b[l] = 0
self.pre(node._left, length,l + 1)
self.b[l] = 1
self.pre(node._right,length,l + 1)
#方法二
# 函数得到每一个叶结点的路径
def binaryTreePaths(self, root):
if not root:#如果root不存在
return []
if not root._left and not root._right:#如果root就是一个叶节点
return [str(root._value)]
pathList = []#用来存储路径
if root._left:#沿左子树下行递归遍历直到到达了叶节点
root._left._codevalue = '0'
pathList+=self.binaryTreePaths(root._left)
self.codeway[root._left._value]=root._left._codevalue
if root._right:
root._right._codevalue='1'
pathList+=self.binaryTreePaths(root._right)
self.codeway[root._right._value] = root._right._codevalue
for index, path in enumerate(pathList):#枚举pathList,得到对应节点路径的存放路径
pathList[index]=str(root._value) + ' ' + path
# for index,path in enumerate(self.codeway):
# self.codeway[index] =str(root._codevalue) + ' ' + path
# print(root._value,root._codevalue)
#用这个打印每一节点对应的编码
return pathList
#生成哈夫曼编码
def code_way(self):
return self.codeway
if __name__=='__main__':
#输入的是字符及其频数
char_weights=[('a',9),('b',12),('c',6),('d',3),('e',5),('f',15)]
tree=HuffmanTree(char_weights)
length=len(char_weights)
#方法二
pathList = tree.binaryTreePaths(tree.root)
codeway=tree.code_way()
print(codeway)
print("路径输出为: ",pathList)
for i in pathList:
i=i.split(' ')[1:]#根节点不参与编码,所以切掉
print("数字 ",i[-1],"的编码是:",end='')
for j in i:
print(codeway[int(j)],end='')
print('\n')
#方法一
tree.pre(tree.root,length,0)
参考
https://blog.csdn.net/wtfmonking/article/details/17150499#