UVA - 1354

G - 天平难题

UVA - 1354

输入房间宽度r，和挂坠数目s , 以及各个挂坠的重量， 用长度为1 的木棍悬挂挂坠或是子天平。

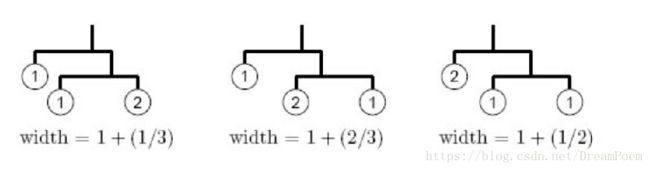
找出一个宽度最宽的天平结构宽度，但不能超出房间宽度，每个子天平，必须是平衡的。

天平的结构是二叉树，叶子节点是挂坠重量

由于挂坠数目1<=s<=6，可以暴力搜索所有可能的结构！！

重点：用位运算表示集合运算

A	B	A&B(交集)	A|B(并集)	A^B(对称差)
二进制	10110	01100	00100	11110
集合	{4，2，1}	{3，2}	{2}	{4，3，2，1}

根据对称差可以求，一个集合的补集

left=set^right;   //left是right关于set的补集

与运算枚举子集

//Set[1..1<0],w[1],w[2],w[3]...,w[n-1]}的所有子集
//Set[0]=0,表示空集,  s[1<set表示Set数组的下标，Set[set]表示W的某一个子集
//Set[subset] 枚举Set[set]的所有子集
for(int subset=set-1; subset ; subset=(subset)&set )
{
    //subset是除了全集和空集的所有子集的状态编码。
}

用二进制枚举幂集

for(int i=0;i<(1<//i是状态编码
    for(int j=0;jif(i&(1<//向S[i]中添加元素w[j]
            s[i]+=w[j];     //s[i] 中的元素是  由状态编码i所确定的元素和
    }
}

n个元素的全集编码为 (1<<n)−1 ( 1 << n ) − 1

例：

i 的二进制形式，看作W集合的状态编码，从最低为到最高为对应W中对应元素在S中的状态，1表示在S中，0表示不在S中。

原因：

当i=(1101)2 当 i = ( 1101 ) 2 时

j=0，i&amp;amp;amp;(1<<0)==(0001)2 j = 0 ， i & a m p ; a m p ; a m p ; ( 1 << 0 ) == ( 0001 ) 2 , w[0]∈S w [ 0 ] ∈ S

j=1,i&amp;amp;amp;(1<<1)==(0000)2 j = 1 , i & a m p ; a m p ; a m p ; ( 1 << 1 ) == ( 0000 ) 2 ,, w[1]∈S w [ 1 ] ∈ S

j=2,i&amp;amp;amp;(1<<2)==(0100)2 j = 2 , i & a m p ; a m p ; a m p ; ( 1 << 2 ) == ( 0100 ) 2 ,, w[2]∈S w [ 2 ] ∈ S

将S看作集合则 S={0，2，3} S = { 0 ， 2 ， 3 } ,

令 W={0，1，2，...，n−1} W = { 0 ， 1 ， 2 ， . . . ， n − 1 }

i从0到1<

思路：每一个子树都是挂坠集合S的一个子集。找到所有子集的排列，计算出各自的天平宽度，进而找出最优解。

计算天平宽度要“递归回溯”更新子天平的宽度

#include
#include
#include
#include
using namespace std;
const int maxn = 6;
struct Tree {
    double L, R;  //当前结点到以当前结点为根的子树的最左/右结点的距离
    Tree(): L(0), R(0) {}
    Tree(int x, int y): L(x), R(y) {}
};

//n个元素的子集有1<
bool vis[1 << maxn];
double r, w[maxn], sum[1 << maxn];
int s;
vector tree[1 << maxn];       //存储以某个集合为根的二叉树子集
void solve(int subset) {
    //这道题的二叉树根节点到最左/右结点的距离，采用回溯的方法更新L, R。
    if(vis[subset])
        return;
    vis[subset] = true;
    bool have_subset = false;       //标记当前subset是否有子集
    for(int left = (subset - 1)⊂ left; left = (left - 1)&subset) {
        //搜索子集
        have_subset = true;
        int right = subset ^ left;  //right 是left关于subset的补集
        double d1 = sum[right] / sum[subset];   //subset的左右子结点距离subset的距离
        double d2 = sum[left] / sum[subset];
        solve(left);
        solve(right);
        //回溯更新L，R
        //下面计算当前结点的L，R
        //根据L，R的定义：当前结点到以当前节点为根结点的子树的左/最右距离
        for(int i = 0; i < tree[left].size(); i++)
            for(int j = 0; j < tree[right].size(); j++) {
                //tree[left],tree[right]内存储了以subset为根节点的所有可能的子结点信息，更新符合条件的tree[subset]
                //这一段更新，很精辟，结合图形理解
                Tree T;
                T.L = max(tree[left][i].L + d1, tree[right][j].L - d2);
                T.R = max(tree[left][i].R - d1, tree[right][j].R + d2);
                if(T.L + T.R < r)
                    tree[subset].push_back(T);
            }
    }
    if(!have_subset)
        tree[subset].push_back(Tree());
}
int main() {
    int t;
    scanf("%d", &t);
    while(t--) {
        scanf("%lf%d", &r, &s);
        for(int i = 0; i < s; i++)
            scanf("%lf", &w[i]);
        for(int i = 0; i < (1 << s); i++) {//枚举子集
            sum[i] = 0;
            tree[i].clear();
            for(int j = 0; j < s; j++)
                if(i & (1 << j)) //向子集中添加元素
                    sum[i] += w[j];
        }
        memset(vis, 0, sizeof(vis));
        int root = (1 << s) - 1;   //自定向下，从全集开始递归
        solve(root);
        double ans = -1;
        for(int i = 0; i < tree[root].size(); i++)
            ans = max(ans, (tree[root][i].L + tree[root][i].R));
        printf("%.10lf\n", ans);
    }
    return 0;
}