《Python深度学习》——第三章 神经网络入门

主要内容：

1. 神经网络核心组件
2. Keras简介
3. 建立深度学习工作站——Jupter
4. 使用深度学习解决二分类，多分类和回归问题

---

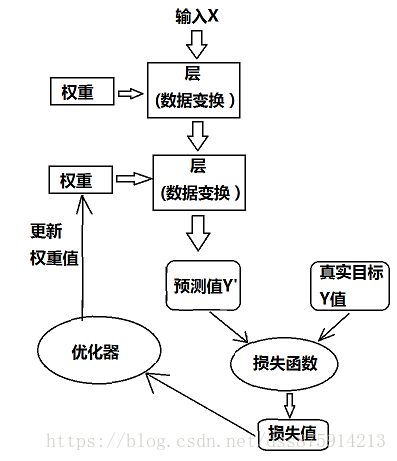
3.1  神经网路剖析

1. 层，多层构成网络
2. 输入函数和目标
3. 损失函数
4. 优化器

3.1.1  层：基本组件

权重

2D张量，用密集连接层（densely  connected  layer）

3D张量，循环层（recurrent layer,如LSTM层）

4D张量，二维卷积层(conv2D)

层兼容性（layer compatiblility）：每一层只接受特定层的输入张量，输出特定形状的张量。

例：layers.Dense(32,input_shape=784,))#输出张量，第一维大小是32。只接受第一维度是784的2D张量。

不写input_shape，自动和上层匹配。

3.1.2  模型：层构成的网络

有向无环图

常见网络拓扑结构（其决定假设空间（hypothesis space））

1. 双分支网络
2. 多头网络
3. Inception模块

选择正确的网络架构是门艺术而不是科学。

3.1.3  损失函数与优化器：配置学习过程的关键

损失函数（目标函数）

优化器：SGD的变体

具有多个输出的神经网络，可以具有多个损失函数，但梯度下降必须基于单个标准损失值，所以要对所有损失函数值求平均。

选择目标函数的指导原则：

二分类问题：二元交叉熵（binary crossentropy）

多分类问题：分类交叉熵（categorical  crossentropy）

回归问题：均方误差（mean-squared error）

序列学习问题：联结主义时序分类（CTC,coonectionist temporal classification）

---

3.2  Keras简介

特点：

1. 相同代码可以在CPU和GPU上无缝切换
2. 具有友好的API
3. 内置支持卷积网络（用于视觉）、循环网络（用于序列处理）以及二者的任意组合
4. 支持任意网络框架：多输入或多输出、层共享、模型共享

3.2.1 Keras、TensorFlow、Theano和CNTK

后端引擎（backend engine）

3.2.2  使用Keras开发：概述

工作流程：

1. 定义训练数据
2. 定义层组合的网络
3. 配置学习过程
4. 调用fit进行迭代

定义模型：

1.Sequential：仅用于层的线性堆叠，常用。

model.add(layers.Dense(32,activation='relu',input_shape=(784,)))

2.函数API：构建任意形式的架构

input_tenser=layer.Input(shape=(784,))

x=layers.Dense(32,activation='relu')(input_tenser)

---

3.3  建立深度学习网络

最好使用UNIX。

3.3.1  Jupyter笔记本：运行深度学习实验的首选方法

3.3.2  运行Keras的两种方法

云端

本地

3.3.3  在云端运行深度学习任务：优点和缺点

3.3.4  深度学习的最佳GPU

NVIDIA  TITAN  Xp

---

3.4  举例

1.二分类

（1）准备数据

转换方法

1. 填充列表
2. 对列表进行one-hot编码

（2）构建网络

Dense(16,activation='relu')

16指隐藏单元（hidden unit）个数

隐藏单元越多，网络能够学到更加复杂的表示，计算代价也越大，且可能过拟合

关键架构：

1. 网络有几层
2. 每层有几个隐藏单元

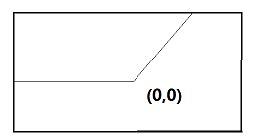
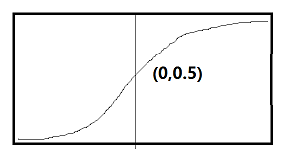
中间层用‘relu’,最后一层用‘sigmoid’（输出0~1）。

引入激活函数是为了：为系统引入非线性。

自定义优化器：通过optimizer传入优化器类实例

自定义损失函数：通过loss和metric传入函数对象

交叉验证：validation_data

（3）进一步实验：

1. 尝试增加或减少隐藏层
2. 尝试增加或减少隐藏单元
3. 改变损失函数
4. 改变激活函数

rmsprop优化器，在任何问题下都可使用。

2.多分类

标签向量化：

1. 整数张量
2. one-hot编码（分类编码（categorical encoding））

中间层维数 一般要大于输出层维数，不然会造成信息瓶颈。

one-hot 编码使用  categorical_crossentropy损失函数

整数标签使用  sparse_categorical_crossentropy

使用 softmax激活函数

3.回归

不同特征取值范围不同，要先标准化

样本数量少，使用小网络,利用K折验证。

最后一层，没有激活函数，是线性层

损失函数：均方误差（MSE,mean squared error）

监控指标：平均绝对误差（MAE,mean absolute error）