知识图谱入门——知识抽取与挖掘（II）
文章首发于博客du_ok’s Notes，本文链接为知识图谱入门——知识抽取与挖掘（II）
本文介绍了一些知识挖掘的方法，包括实体消歧与链接、知识规则挖掘和知识图谱表示学习。
知识抽取之后可以获得一些结构化的知识，而知识挖掘则是从结构化的知识推理出新的知识，例如挖掘出新的实体、新的关联规则等。
- 知识的消歧与链接：基于内容的挖掘
- 知识规则挖掘：基于结构的挖掘
- 知识图谱表示学习
实体消歧与链接
目前对实体消歧的研究往往通过实体链接的方式，将有歧义的实体映射到一个无歧义的目标实体。
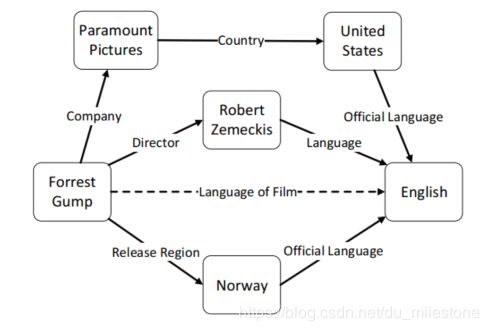
首先给出一个例子：给定一篇文本中的实体指称（mention），确定这些指称在给定知识库中的目标实体（entity）。
实体链接的主要流程如下：
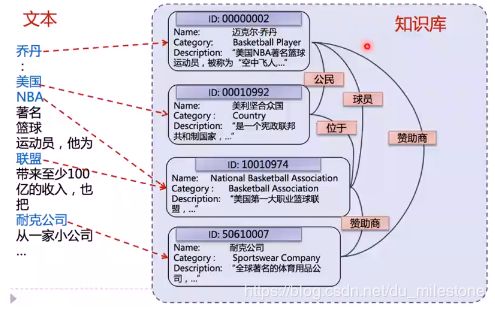
实体引用表： 从mention到entity ID的映射表。如将乔丹与ID为2的实体的映射就是实体引用表中的一个示例。
作用：查找出某一实体在知识库中对应的别名、简称、和同义词等。（可能存在错误）
对于实体的链接主要主要工作是候选实体的生成（图中蓝色的即为候选实体）和候选实体的消歧（如区分出UCB的乔丹和篮球之神乔丹）。
基于entity-mention模型消歧（生成概率模型）
基于百科型知识库，适用于长、短文本场景。
在知识库中有两个乔丹实体，分别是篮球之神和ML大神。在下面的两个文本中提及到的Jordan和Michael Jordan都可以对应到知识库里面的两个实体，这就是刚刚所说的实体引用表。接着我们就可以得出文本中的Jordan的两个候选实体分别是Michael Jeffrey Jordan和Michael I. Jordan。之后我们就需要消歧得到所对应的唯一确定的实体 e e e。
e = arg max e P ( m , e ) P ( m ) e = \arg\max\limits_{e} \frac{\mathrm{P}(m, e)}{\mathrm{P}(m)} e=argemaxP(m)P(m,e)
可以转换成：
e = arg max e P ( m , e ) = arg max e P ( e ) P ( s ∣ e ) P ( c ∣ e ) e = \arg\max\limits_{e} \mathrm{P}(m ,e) = \arg\max\limits_{e} \mathrm{P}(e) \mathrm{P}(s|e)\mathrm{P}(c|e) e=argemaxP(m,e)=argemaxP(e)P(s∣e)P(c∣e)
e e e为实体， s s s为名字， c c c为context。
- 先验概率 P ( e ) \mathrm{P}(e) P(e)：通过活跃度（popularity）来计算；
- ( s ∣ e ) \mathrm(s|e) (s∣e)可以通过调用实体引用表中s作为锚文本出现的概率。
- P ( c ∣ e ) \mathrm{P}(c|e) P(c∣e)通过上下文计算翻译概率。（不太理解）
这样可以将上述例子描述为：给定一个m求生成e的概率，此处即为给定一个文本“Jordan joins Bulls in 1984.”，其中提及为“Jordan”，通过计算由Jordan生成Michael Jeffrey Jordan的概率和Michael I. Jordan的概率，概率大的为最终的结果。
简单来说就是根据mention所处的句子和上下文来判断该mention是某一实体的概率。
基于实体关联图与标签传播算法消歧
基于百科型知识库，适用于长文本场景。
实体关联图由3个部分组成：
- 每个顶点 V i = ⟨ m i , e i ⟩ V_i=\langle m_i, e_i \rangle Vi=⟨mi,ei⟩由mention-entity对构成；
- 每个顶点得分 ：代表实体指称 m i m_i mi的目标实体为 e i e_i ei概率可能性大小；
- 每条边的权重：代表语义关系计算值，表明顶点 V i V_i Vi和 V j V_j Vj的关联程度。
基于实体关联图消歧具体过程如下：
-
顶点的得分的初始化
- 若顶点V实体不存在歧义，则顶点得分设置为1，如图中最左边的两个结点；
- 若顶点中mention和entity满足 p ( e ∣ m ) > = 0.95 \mathrm{p}(e|m)>=0.95 p(e∣m)>=0.95，则顶点得分也设置为1。
- 其余顶点的得分设置为 p ( e ∣ m ) \mathrm{p}(e|m) p(e∣m)。
-
标的权重的初始化：基于深度语义关系模型
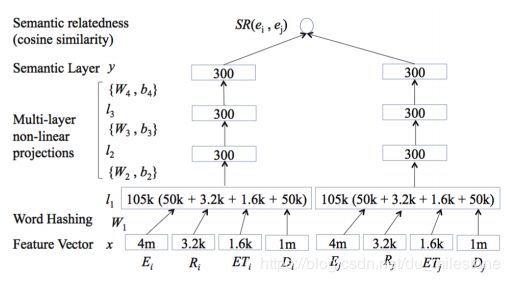
- 此处可以使用Wikipedia作为知识库，由于Wikipedia既包含结构化数据有包括非结构化数据，很适合作为训练数据来训练。
- E: entity, R: relation, ET: entity type, D: word.
- 首先通过Word Hashing将上述变量转换为特征向量（类似于embedding？），接着做多层非线性投影（如使用sigmoid等函数）得到语义层；最后计算语义的相似度（如计算余弦相似度）作为两个实体之间的权重。
-
基于图的标签传播算法
如上算法可以分为两步：- 构造相似矩阵
- 迭代传播直到收敛算法结束
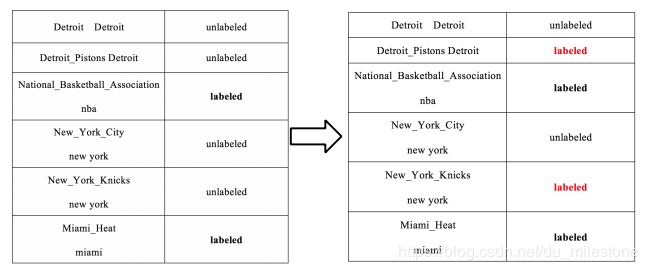
若某些mention没有多个候选实体，则可认为它是labeled：图中nba可认为是labeled，而new york有两个候选实体所以认为是unlabeled；
将labeled数据（一般多个）的影响向外传播，形成了一种协同传播，相当于构建了一个相似矩阵；
对图进行regulation，直到每一个标签都稳定了，起到协同消歧的作用。
基于实体关联图和动态PageRank算法消歧
基于百科型知识库，适用于长文本场景。
基本流程如下：
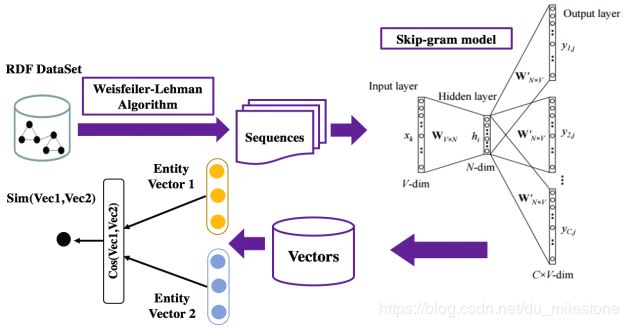
- 基于RDF三元组的数据库，离线将RDF三元组转换成实体向量（如使用woed2vec、知识图谱表示学习等方法）；
- 根据实体向量计算相似度，并构建实体关联图；
- 使用基于图的动态PageRank算法更新图。
候选实体语义相似度计算：
总体的思想是先将RDF转换成vector，接着计算vector之间的余弦相似度。
- Weisfeiler-Lehman Algorithm：将RDF图转换成子图，再将子图转换成序列；
- Skip-gram model：The Skip-gram model architecture usually tries to achieve the reverse of what the CBOW model does. It tries to predict the source context words (surrounding words) given a target word (the center word);
- 计算余弦相似度。
构建实体关联图：
实体关联图由四个部分组成：
- 实体指称节点
- 候选实体节点
- 候选实体节点顶点值：代表该候选实体是实体指称的目标实体概率大小
- 候选实体节点边权值：代表两个候选实体间的转化概率大小
构建过程：
- 各候选实体节点值：初始化均相等，之后每一轮更新为上一轮PageRank得分。
- 候选实体节点边权值：
- 计算两个实体之间相似度大小：
S M ( e a i , e b j ) = c o s ( v ( e a i ) , v ( e b j ) ) SM(e^{i}_{a}, e_{b}^{j} ) = cos (v(e^{i}_{a}), v(e_{b}^{j})) SM(eai,ebj)=cos(v(eai),v(ebj)) - 计算两个候选实体之间转换概率：
E T P ( e a i , e b j ) = S M ( e a i , e b j ) Σ k η ( v , v i ) S M ( e a i , k ) ETP(e^{i}_{a}, e_{b}^{j} ) = \frac{SM(e^{i}_{a}, e_{b}^{j} )}{\Sigma_{k\eta(v, v_{i})} SM(e^{i}_{a},k)} ETP(eai,ebj)=Σkη(v,vi)SM(eai,k)SM(eai,ebj)
- 计算两个实体之间相似度大小：
更新实体关联图：
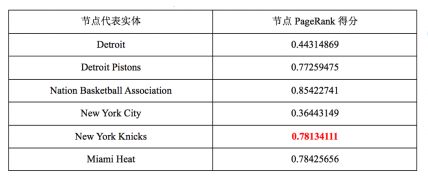
选择本轮最高得分的未消歧实体 New York Knicks作为实体指称New York的最佳实体，删除其他候选实体 New York City及相关的边，更新图中的边权值。
小结
- 知识库的变更：从百科知识库发展到特定领域知识库
- 实体链接的载体：从长文本到短文本，甚至到列表和表格数据
- 候选实体生成追求同义词、简称、各种缩写等的准备和高效从Mention到实体候选的查找
- 实体消歧则考虑相似度计算的细化和聚合，以及基于图计算协同消歧
知识规则挖掘
- 基于归纳逻辑编程 (Inductive Logic Programming, ILP)的方法
- 使用精化算子 (refinement operators)
- 基于统计关系学习 (Statistical Relational Learning, SRL)的方法
- 主要对贝叶斯网络进行扩展
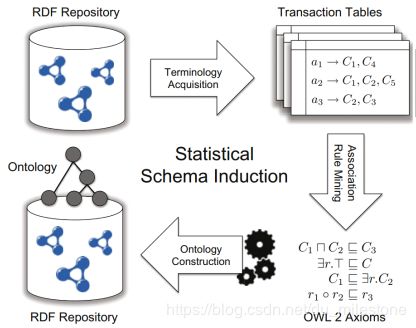
- 基于关联规则挖掘 (Association Rule Mining，ARM)的方法
- 构建事务表
- 挖掘规则
- 将规则转换为OWL公理
- 构建本体
基于关联规则挖掘（ARM）
示例：
| 公理（Axiom） | 规则（rules） |
|---|---|
| C ∈ D \mathrm{C}\in\mathrm{D} C∈D | { C } ⇒ { D } \{\mathrm{C}\}\Rightarrow\{\mathrm{D}\} {C}⇒{D} |
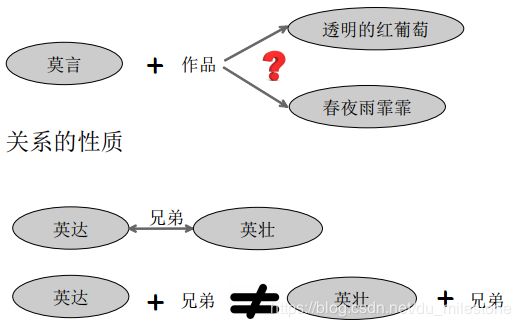
规则 { C } ⇒ { D } \{\mathrm{C}\}\Rightarrow\{\mathrm{D}\} {C}⇒{D}意味着：概念C的实例同时属于概念D，规则的置信度越高，则公理 C ∈ D \mathrm{C}\in\mathrm{D} C∈D的可能性越大。
- 置信度等详见频繁项集
- 支持度： 指某频繁项集在整个数据集中的比例。假设数据集有 10 条记录，包含{‘鸡蛋’, ‘面包’}的有 5 条记录，那么{‘鸡蛋’, ‘面包’}的支持度就是 5/10 = 0.5。
- 置信度： 是针对某个关联规则定义的。有关联规则如{‘鸡蛋’, ‘面包’} -> {‘牛奶’}，它的置信度计算公式为{‘鸡蛋’, ‘面包’, ‘牛奶’}的支持度/{‘鸡蛋’, ‘面包’}的支持度。假设{‘鸡蛋’, ‘面包’, ‘牛奶’}的支持度为 0.45，{‘鸡蛋’, ‘面包’}的支持度为 0.5，则{‘鸡蛋’, ‘面包’} -> {‘牛奶’}的置信度为 0.45 / 0.5 = 0.9。(详见Reference)
上图可以推出Airport属于Building。
基于统计关系学习（SRL）
输入：（实际上就是一个KG）
- 实体集合 { e i } \{e_i\} {ei}
- 关系集合 { r k } \{r_k\} {rk}
- 已知的三元组集合 { ( e i , r k , e j ) } \{(e_i, r_k, e_j)\} {(ei,rk,ej)}
目标：根据已知的三元组对给定的未知的三元组成立的可能性进行预测，可用于知识图谱的补全。
若 e i , e j e_i,e_j ei,ej之间没有申明关系 r k r_k rk，而计算出来的 P ( e i , r k , e j ) \mathrm{P}(e_i, r_k, e_j) P(ei,rk,ej)很高（如P=1），则认为可以补全这条关系。
接下来主介绍一种基于图的统计关系学习，它的基本思想是：
- 将连接两个实体的路径作为特征来预测其间可能存在的关系。
给出一个简单的知识图谱的图如下，图谱中的边是一个有向的图，为了使图中可以形成路径，在图中定义了一些逆关系（如 i s A − 1 isA^{-1} isA−1）。在这个图中我们希望可以通过其他的三元组推出Charlotte也是一个Writer。
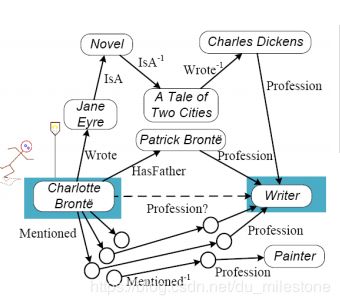
给出一个通用关系学习框架如下：
在基于图的方法中我们采用了的Relational Learning Algorithm是路径排序算法（Path Ranking Algorithm）。
我们定义G=(N,E, R):
- N: nodes (instances or concepts)
- E: edges
- R: edge types
Note: r − 1 r^{-1} r−1: reverse of edge type r
接着定义Path type π : ⟨ r 1 , r 2 , . . . , r n ⟩ \pi:\langle r_1, r_2,..., r_n \rangle π:⟨r1,r2,...,rn⟩:
e.g.
在前面给出的图中，我们可以通过如
对于这个实体对的概率可以通过如下公式计算：
s c o r e ( s , t ) = ∑ π ∈ Q P ( s → t ; π ) Θ π score(s, t) = \sum_{\pi \in Q}P(s \to t; \pi)\Theta_{\pi} score(s,t)=π∈Q∑P(s→t;π)Θπ
- Q Q Q：是所有起始为s终点为t的路径集合（限制路径的最大长度为n）
- Θ π \Theta_{\pi} Θπ：通过训练得到的路径权重
路径概率的计算：
P ( s → t ; π ) = ∑ P ( s → z ; π ′ ) P ( z → t ; r ) P(s \to t; \pi) = \sum P(s \to z; \pi^{'})P(z \to t; r) P(s→t;π)=∑P(s→z;π′)P(z→t;r)
- 将s到t的路径细化成s到z和z到t两条路径，其中z到t是存在关系r的单跳路径
- 具体使用动态规划的方法求解
训练权重的计算（离线计算）：
可以将路径作为特征，进行逻辑回归来求得权重。
最后通过计算出来的P的大小判断出(Charlotte Bonte, Writer)是成立的。
知识图谱表示学习
知识图谱表示学习的意义
在自然语言处理中我们可以通过word embedding、sentence embedding甚至是document embedding来建立一个低维的统一的语义空间，使得语义可以计算。
在知识图谱中也类似，可以做：
-
实体预测与推理
给定一个实体和一个关系→预测另外一个实体。
如给定一个电影实体《卧虎藏龙》和一个关系“观影人群”，来预测另外一个实体是什么。 -
关系推理
-
推荐系统
知识图谱表示学习模型——TransE
TransE模型
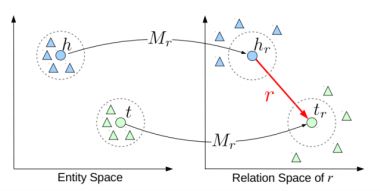
TransE（Translation Embedding）是基于实体和关系的分布式向量表示，将三元组 ( h e a d ， r e l a t i o n ， t a i l ) (head，relation，tail) (head，relation，tail)看成向量h通过r翻译到t的过程，通过不断的调整向量h、r和t，使h+r尽可能与t相等。
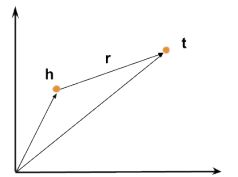
如给出三元组Capital of(Beijing, China)和Capital of(Pairs, France)，则可以得出如下向量表示：
B e i j i n g − C h i n a = P a i r s − F r a n c e = C a p i t a l o f Beijing-China = Pairs-France = Capital \ of Beijing−China=Pairs−France=Capital of
TransE的优化目标：
- 势能函数： f ( h , r , t ) = ∣ ∣ h + r − t ∣ ∣ 2 f(h, r, t) = ||h+r-t||_2 f(h,r,t)=∣∣h+r−t∣∣2
f ( B e i j i n g , C a p i t a l − o f , C h i n a ) < f ( S h a n g h a i , C a p i t a l − o f , C h i n a ) f(Beijing, Capital-of, China) < f(Shanghai, Capital-of, China) f(Beijing,Capital−of,China)<f(Shanghai,Capital−of,China) - 目标函数：为了使知识库中定义的势能比不在知识库中的三元组的势能低，即最小化整体势能。
min ∑ ( h , r , t ) ∈ Δ ∑ ( h ′ , r ′ , t ′ ) ∈ Δ ′ [ γ + f ( h , r , t ) − f ( h ′ , r ′ , t ′ ) ] + \min \sum_{(h,r,t) \in \Delta} \sum_{(h^{'},r^{'},t^{'}) \in \Delta^{'}} [\gamma+f(h,r,t)-f(h^{'},r^{'},t^{'})]_+ min(h,r,t)∈Δ∑(h′,r′,t′)∈Δ′∑[γ+f(h,r,t)−f(h′,r′,t′)]+
[ X ] + = max ( 0 , x ) [X]_+=\max(0, x) [X]+=max(0,x)
TransE的缺陷： 无法处理一对多、多对一和多对多问题。
TransE模型改进
实体语义空间投影
-
TransH：将头尾实体映射到一个超平面
-
TransR：通过矩阵变换，将头、尾实体映射到一个新的语义空间，使得这个空间的关系尽量保持一对一。
分而治之（有关属性的表示）
对于知识图谱的边既可以是属性（data type property）也可以是关系（object property）。对于属性来说，很容易产生一对多（如喜好）和多对一（性别），若将关系和属性的表示会出现困难。
分而治之就是将对属性的学习和对关系的学习做了一个区分，同时基于属性的学习可以推进对关系的学习。
路径的表示学习
**PRA vs. TransE：**两种方法存在互补性
PRA：可解释性强；能够从数据中挖掘出推理规则；难以处理稀疏关系；路径特征提取效率不高。
TransE：能够表示数据中蕴含的潜在特征；参数较少，计算效率较高；模型简单，难以处理多对一、一对多、多对多的复杂关系可解释性不强。
性能比较
加入规则的表示学习
Logical connectives：学习推理的规则，是推理的规则似然最大化。
多模态的表示学习
助力Zero-Shot和长尾链接预测：对于在KG中出现很少，甚至没有出现过，而在长文本中出现较多的长尾数据来做实体链接预测。
- h s h_s hs：KG中结构的学习
- h d h_d hd：在文本中的描述的学习，此处使用了Bi-LSTM
基于知识图谱结构的表示学习
考虑哪些数据可以用来描述实体：
- 实体周围的实体
- 从一个实体到这个实体的联通路径
Neighbor Context：
Path Context：
Triple Context = Triple + Path Context + Neighbor Context
- 势能函数
- 希望三元组在Triple Context概率最大
f ( h , r , t ) = P ( ( h , r , t ) ∣ C ( h , r , t ) ; Θ ) f(h,r,t)=P((h,r,t)|C(h,r,t);\Theta) f(h,r,t)=P((h,r,t)∣C(h,r,t);Θ) - 假设不同的Context都是相互独立的企且独立用来描述三元组的某一部分
f ( h , r , t ) = P ( h ∣ C ( h , r , t ) ; Θ ) P ( t ∣ C ( h , r , t ) , h ; Θ ) P ( r ∣ C ( h , r , t ) , h , t ; Θ ) \begin{aligned} f(h,r,t) = & P(h|C(h,r,t);\Theta) \\ & P(t|C(h,r,t),h;\Theta) \\ & P(r|C(h,r,t),h,t;\Theta) \end{aligned} f(h,r,t)=P(h∣C(h,r,t);Θ)P(t∣C(h,r,t),h;Θ)P(r∣C(h,r,t),h,t;Θ)
f ( h , r , t ) ≈ P ( h ∣ C N ( h ) ; Θ ) ⋅ P ( t ∣ C P ( h , t ) , h ; Θ ) ⋅ P ( r ∣ h , t ; Θ ) f(h,r,t) \approx P(h|C_N(h);\Theta) \cdot P(t|C_P(h,t),h;\Theta) \cdot P(r|h,t;\Theta) f(h,r,t)≈P(h∣CN(h);Θ)⋅P(t∣CP(h,t),h;Θ)⋅P(r∣h,t;Θ)
- 目标函数
P ( K ∣ Θ ) = Π ( h , r , t ) ∈ K f ( h , r , t ) P(\mathcal{K}|\Theta) = \Pi_{(h,r,t)\in \mathcal{K}}f(h,r,t) P(K∣Θ)=Π(h,r,t)∈Kf(h,r,t)
总结与挑战
- 融合更多本体特征的知识图谱表示学习算法研发
- 知识图谱表示学习与本体推理之间的等价性分析
- 知识图谱学习与网络表示学习之间的异同
- 神经符号系统
Reference
- 王昊奋《知识图谱》
- 频繁项集与关联规则 FP-growth 的原理和实现